
- •Методические указания практическим занятиям
- •Практическое занятие №1 Формула Коши
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №2 временные и частотные характеристики автоматических систем (ас)
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №3 структурные схемы автоматических систем (ас)
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №4 теория устойчивости движения
- •Краткие теоретические сведения
- •Теорема Ляпунова об устойчивости по первому приближению
- •Критерий Гурвица
- •Критерий устойчивости Михайлова
- •Задачи для самостоятельного решения
- •Практическое занятие №5 Уравнение Эйлера
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №6 Уравнение Эйлера-Пуассона
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №7 Вариационные задачи на условный экстремум
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №8 Принцип максимума Понтрягина
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №9 Динамическое программирование
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Билиографический список
- •Методические указания к практическим занятиям по дисциплине
Задачи для самостоятельного решения
Используя теорему Ляпунова об устойчивости по первому приближению, исследовать на устойчивость нулевое решение следующих систем:
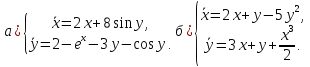
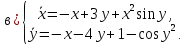
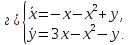
Используя критерий устойчивости Гурвица, исследовать на устойчивость нулевое решение следующих уравнений:
а)
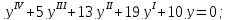
б)
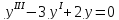 ;
;
в)
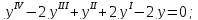
г)
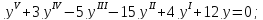
При каких значениях
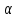 будет устойчиво нулевое решение
уравнений:
будет устойчиво нулевое решение
уравнений:
а)
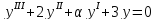 ;
;
б)
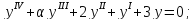
в)
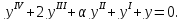
При каких значениях
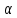 и
и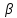 будет устойчиво нулевое решение
уравнений:
будет устойчиво нулевое решение
уравнений:
а)
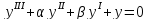 ;
;
б)
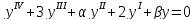 .
.
Используя критерий устойчивости Михайлова, исследовать на устойчивость нулевое решение
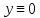 уравнений:
уравнений:
а)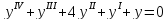 ;
;
б)

в)
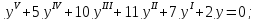
г)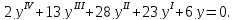
Практическое занятие №5 Уравнение Эйлера
Цель занятия: Решение задачи об оптимальном управлении в случае функционала, зависящего от производной первого порядка.
Краткие теоретические сведения
Исследуется на экстремум, критерий следующего вида :
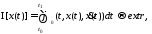 (5.1)
(5.1)
где
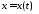 –траектория развития управляемого
процесса;
–траектория развития управляемого
процесса;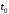 –
начало функционирования процесса;
–
начало функционирования процесса;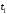 –
окончание функционирования процесса;
–
окончание функционирования процесса;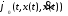 –
некоторая известная функция своих
аргументов.
–
некоторая известная функция своих
аргументов.
Являются заданными начальное и конечное состояния процесса:
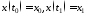 .
(5.2)
.
(5.2)
Задача (5.1),(5.2) называется вариационной задачей с закрепленными граничными точками. Решение данной задачи находится из решения уравнения Эйлера, которое имеет вид
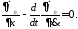
В развёрнутом виде уравнение Эйлера представлено следующим выражением:
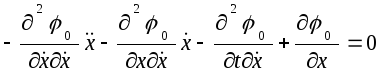 . (5.3)
. (5.3)
Решение
уравнения Эйлера ищется в виде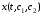 ,
где
,
где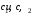 –const,
определяемые из условий (5.2).
–const,
определяемые из условий (5.2).
Пример решения задачи. Эффективность химико-технологического процесса определяется критерием вида
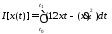 ,
(5.4)
,
(5.4)
где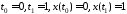 ;
;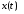 – траектория развития процесса,
– траектория развития процесса,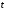 –
время его функционирования. Требуется
найти явный вид траектории
–
время его функционирования. Требуется
найти явный вид траектории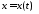 ,
которая доставляет экстремум критерию
(5.4), при
,
которая доставляет экстремум критерию
(5.4), при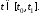
Решение: Запишем уравнение Эйлера в развернутом виде:
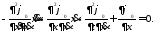
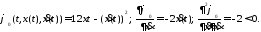
Согласно
условию Лежандра, необходимым условием
максимума или минимума
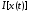 является
выполнение соответствующих условий:
является
выполнение соответствующих условий: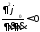 или
или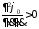 .
Таким образом
.
Таким образом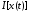 достигает максимума:
достигает максимума:
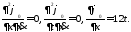
Получаем неоднородное уравнение:
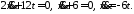
Решение данного уравнения представляется в виде
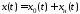 ,
,
где
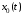 – решение однородного уравнения,
– решение однородного уравнения,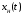 – частные решения неоднородного
уравнения. Решение однородного уравнения
– частные решения неоднородного
уравнения. Решение однородного уравнения ищем в виде
ищем в виде
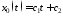 ,
,
где
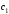 и
и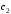 –const,
определяемые из начальных условий.
Решение неоднородного уравнения будем
искать в виде
–const,
определяемые из начальных условий.
Решение неоднородного уравнения будем
искать в виде
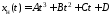 ,
,
где A,B,C,D могут быть найдены, например, методом неопределенных коэффициентов:
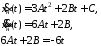
Приравняем коэффициенты при одинаковых степенях t:
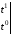
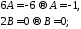
C и D – могут быть любыми, положим, например, C=D=0. Тогда получаем окончательно:
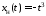 ,
,
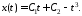
Определим
константы
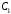 и
и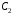 из начальных условий
из начальных условий
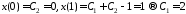
Тогда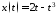 –
оптимальная траектория развития
управляемого процесса, доставляющая
максимум критерию (5.4).
–
оптимальная траектория развития
управляемого процесса, доставляющая
максимум критерию (5.4).
Задачи для самостоятельного решения
1.На каких кривых достигают экстремум следующие функционалы:
1)
J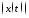

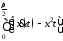
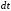 ,
,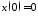 ,
,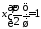 ;
;
2)
J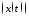

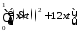
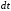 ,
,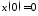 ,
,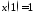 ;
;
3)
J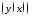

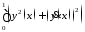
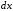 ,
,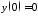 ,
,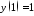 ;
;
4)
J

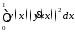 ,
,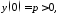
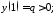
5)
J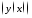

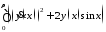
 ,
,
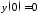 ,
,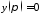 .
.
Практическое занятие №6 Уравнение Эйлера-Пуассона
Цель занятия: Решение задачи об оптимальном управлении в случае функционала, зависящего от производных более высоких порядков.
Краткие теоретические сведения
Предположим, что требуется исследовать на экстремум критерий вида :
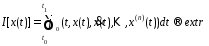 ,
(6.1)
,
(6.1)
где
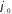 – известная функция своих
аргументов;
– известная функция своих
аргументов;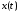 –траектория
развития процесса;
–траектория
развития процесса;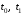 – начальные и конечные моменты времени.
– начальные и конечные моменты времени.
Будем
также предполагать, что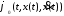 –
непрерывна иn+2
раза дифференцируемая по всем своим
аргументам функция. Граничные условия
имеют вид:
–
непрерывна иn+2
раза дифференцируемая по всем своим
аргументам функция. Граничные условия
имеют вид:
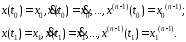 (6.2)
(6.2)
Решение задачи (6.1)-(6.2) определяется из решения уравнения Эйлера-Пуассона, которое имеет вид:
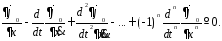
Пример решения задачи. Управляемый процесс оценивается критерием вида:
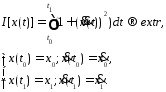
Найти оптимальную траекторию развития процесса.
Решение.
Запишем
следующее уравнение: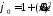 ,
для которого уравнение Эйлера-Пуассона
имеет вид:
,
для которого уравнение Эйлера-Пуассона
имеет вид:
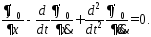
При
взятии дифференциала
 порядок
производной наращивается, т.е.
порядок
производной наращивается, т.е.
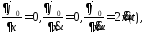
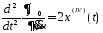 ,
,
окончательно получаем:
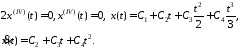
Пусть, например, t0=0, t1=1 и заданы начальные условия вида:
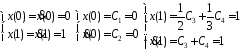
Решая данную
систему, получаем: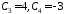 ,
т.е. данный критерий эффективности
достигает экстремума на кривой вида
,
т.е. данный критерий эффективности
достигает экстремума на кривой вида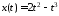 .
.
