Задача 1.5.1
Решите следующие задачи выпуклого программирования. Дайте интерпретацию двойственным переменным и проинтерпретируйте выполнение условий дополняющей нежесткости. Как изменится оптимальное решение при изменении правых частей ограничений?
Решение:
1. Геометрическое решение:
Областью допустимых решений задачи является замкнутая выпуклая область ВСО:
Линии уровня
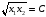представляют собой ветви гиперболы
,
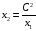расположенные в 1-м квадранте системы
координат. При возрастании значения С
гиперболы
сдвигаются вверх и вправо. Таким
образом, максимальное значение С
достигается в точке, где гипербола
касается прямой
.
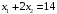Составляем функцию от одной переменной и находим точки экстремума.
.
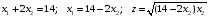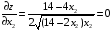при x2
= 3,5. Тогда
x1
= 14–2∙3,5
= 7.
Следовательно,
точка касания А(7; 3,5) является точкой
максимума функции
при
условии
.
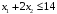Значение функции в точке максимума равно
.
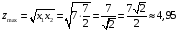Решение с помощью функции Лагранжа.
Ограничение
записываем в виде
.
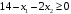Составляем функцию Лагранжа:
.
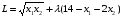Записываем необходимые условия для максимума:
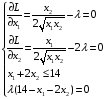
Решаем систему:
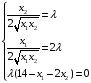
Из 3-го уравнения (условие дополняющей нежёсткости) получаем:
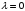или
.
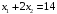Если
,
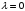то получаем
;
.
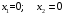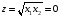Если
,
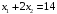то решаем систему:
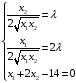
Выражая из 1-го и
2-го уравнения
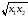и приравнивая полученные выражения,
получим:
.
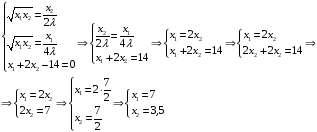
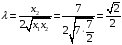Значение целевой функции на этом решении равно
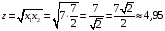и является
максимальным в заданной области.
Двойственная
переменная
.
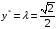Седловая
точка функции Лагранжа
,
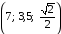т.е.
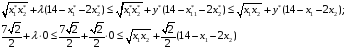
Ограничение
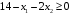является активным,
.
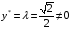Если
уменьшать правую часть ограничения
,
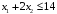то оптимальное
решение будет уменьшаться, а если
увеличивать
правую часть, то оптимальное
решение будет увеличиваться.
.
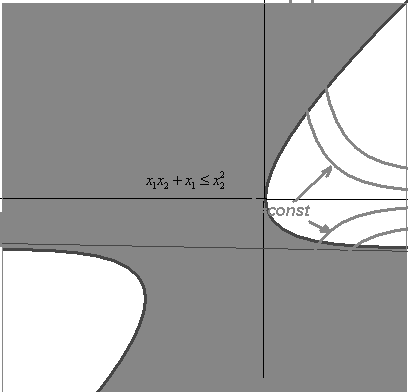
Множество допустимых значений не является выпуклым, даже при условии неотрицательности всех переменных. На нем целевая функция может быть как угодно велика, 2 линии уровня на рисунке
Дополним этот вывод аналитическим решением. Функция Лагранжа дифференцируема по всем своим переменным, как следствие теоремы Куна-Таккера, либо все ее частные производные должны быть равны 0, либо двойственная переменная у=0. Последний случай тривиален, тогда целевая функция тоже равна 0 , и это не максимум. Получаем систему необходимых условий:
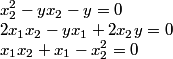
Из первого и третьего уравнений
Подставим во второе уравнение
кроме тривиального случая, когда целевая
функция =0, получаем
,
при этом целевая функция
отрицательна, и это тоже не максимум.
Ответ: максимум не существует.
Задача 2.1.1 и 2.1.2
2.1.1. Для данных множеств исходов и описанных предпочтений выясните, являются ли предпочтения рациональными и можно ли их представить функцией полезности?
2.1.2. Найдите результат выбора, если он существует.
Решение:
O ={a, b, c}– множество возможных исходов.
a ≻ c – альтернатива a лучше альтернативы c,
a ≻ b – альтернатива a лучше альтернативы b,
b ~ c – b эквивалентно c (индивидуум безразличен в выборе между b и c).
Предпочтения являются рациональными, если индивидуум всегда может сравнить любую пару альтернатив. В данном случае предпочтения являются рациональными.
Следовательно, информации достаточно, чтобы сравнить любую пару альтернатив. Зададим функцию полезности, т.е. сопоставим каждому из возможных исходов некоторое число таким образом, чтобы выполнялось следующее свойство:
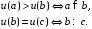
Наибольшую полезность будет иметь исход a, исходы b и с должны иметь одинаковую полезность. Функция полезности может быть задана, например, следующим образом: u(a) = 2, u(b) =1, u(с) = 1.
В данном случае наилучший выбор – альтернатива a, т.к. она имеет наибольшую полезность.