
- •Задача 1.1.5
- •Задача 1.2.1
- •Задача 1.2.4
- •Задача 1.3.1
- •Задача 1.4.1
- •Задача 1.4.2
- •Задача 1.4.3
- •Задача 1.5.1
- •1. Геометрическое решение:
- •Задача 2.1.1 и 2.1.2
- •Задача 2.2.1
- •Задача 2.2.6
- •Задача 2.3.1
- •Таким образом, оба варианта убыточны в среднем, но менее убыточны вложения в изделие в
- •Задача 2.3.6
- •Задача 2.4.1
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Контрольная работа
По дисциплине: Оптимизация и математические методы принятия решений
Выполнил:
Группа:
Вариант: 1
Проверил: ___________________
Новосибирск, 2012 г
Задача 1.1.1
Решите задачу о диете со следующими данными. Из продуктов трех видов необходимо составить рацион минимальной стоимости, соблюдя при этом ограничения по содержанию некоторых витаминов. Данные приведены в таблице:
|
|
Продукты |
Суточная потребность |
|||
|
1 |
2 |
3 |
|
||
|
Е |
3 |
2 |
1 |
14 |
|
|
F |
3 |
4 |
5 |
10 |
|
|
РР |
1 |
5 |
2 |
8 |
|
|
Цента продукта |
8 |
12 |
11 |
|
|
Решение:
Обозначим через x1 количество первого продукта, а через x2 – количество второго продукта, x3 – количество третьего продукта, включаемых в ежедневный рацион. Приходим к задаче:
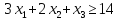
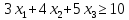

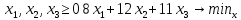
Приведем систему неравенств к канонической форме путем введения дополнительных базисных переменных. В 1-м неравенстве вводим базисную переменную x4 со знаком минус. В 2-м неравенстве вводим базисную переменную x5 со знаком минус. В 3-м неравенстве вводим базисную переменную x6 со знаком минус.
3x1 + 2x2 + x3 – 1x4 + 0x5 + 0x6 = 14
3x1 + 4x2 + 5x3 + 0x4 – 1x5 + 0x6 = 10
x1 + 5x2 + 2x3 + 0x4 + 0x5 – 1x6 = 8
Умножим все строки на (-1) и будем искать первоначальный опорный план.
–3x1 – 2x2 – x3 + 1x4 – 0x5 – 0x6 = –14
–3x1 – 4x2 – 5x3 – 0x4 + 1x5 – 0x6 = –10
–x1 – 5x2 – 2x3 – 0x4 – 0x5 +1x6 = –8
Введем новую переменную x0 = –8x1–12x2–11x3.
Выразим базисные переменные <4, 5, 6> через небазисные.
x0 = 0-8x1-12x2-11x3 x4 = -14+3x1+2x2+x3
x5 = -10+3x1+4x2+5x3 x6 = -8+x1+5x2+2x3
Среди свободных членов в системе уравнений есть отрицательные элементы. Используем двойственный симплекс-метод. Выберем из них наибольший по модулю, а в его уравнении – любой отрицательный.
Чтобы теперь выразить все переменные через небазисные, в выражении для x4 выразим x1 и подставим полученное выражение во все остальные равенства.
x0 = -37,33-6,67x2-8,33x3-2,67x4 x1 = 4,67-0.67x2-0,33x3+0,33x4
x5 = 4+2x2+4x3+x4 x6 = -3,33+4,33x2+1,67x3+0,33x4
Среди свободных членов в системе уравнений есть отрицательные элементы. Используем двойственный симплекс-метод. Выберем из них наибольший по модулю, а в его уравнении – любой отрицательный.
Чтобы теперь выразить все переменные через небазисные, в выражении для x6 выразим x2 и подставим полученное выражение во все остальные равенства.
x0 = -42,46-5,77x3-2,15x4-1,54x6
x1 = 4,15-0,0769x3+0,38x4-0,15x6
x5 = 5,54+3,23x3+0,85x4+0,46x6
x2 = 0,77-0,38x3-0,0769x4+0,23x6
В базисном столбце все элементы положительные. Переходим к основному алгоритму симплекс-метода. Поскольку задача решается на максимум, то переменную для включения в текущий план выбирают по максимальному положительному числу в уравнении для x0. Выражение для x0 не содержит положительных элементов. Найден оптимальный план.
Окончательный вариант системы уравнений:
x0 = -42,46-5,77x3-2,15x4-1,54x6
x1 = 4,15-0,0769x3+0,38x4-0,15x6
x5 = 5,54+3,23x3+0,85x4+0,46x6
x2 = 0,77-0,38x3-0,0769x4+0,23x6
Оптимальный план можно записать так:
x1 = 4,15 x5 = 5,54 x2 = 0,77
F(X) = 8*4,15 + 12*0,77 = 42,46
Стоимость рациона не может быть меньше, чем 42,46 денежных единиц.
Задача 1.1.5
Приведите следующие задачи к каждой из канонических форм, описанных в лекции:
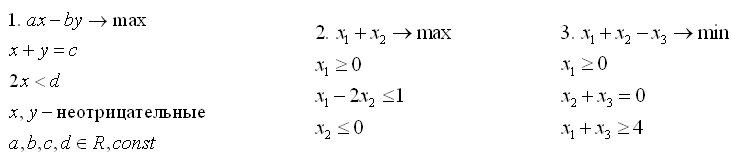
Решение:
-
В задаче №1 одно из ограничений задано в виде равенства, а другое – в виде неравенства.
Запишем
условие
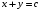 в виде пары неравенств:
в виде пары неравенств:
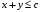 и
и
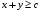 .
.
Второе
неравенство умножением на –1 приведём
к виду
 .
.
Получаем каноническую форму задачи на максимум, в которой все ограничения заданы в виде неравенств вида ≤:
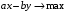
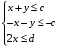
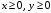
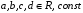
Каноническую форму задачи на минимум, в которой все ограничения заданы в виде неравенств вида ≥, получим, умножая целевую функцию и каждое неравенство на –1:
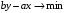

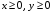
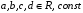
Каноническую форму задачи, в которой все ограничения заданы в виде равенств, получим, введя новую неотрицательную переменную z:
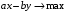
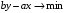
 или
или
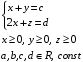
2. Для приведения задачи к канонической форме необходимо:
Привести целевую функцию к минимизации умножением на (-1)

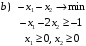
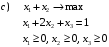

3. Т.к. переменные x2 и x3 могут принимать как положительные, так и отрицательные значения, заменим их разностями новых неотрицательных переменных.
Т.к.
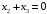 ,
т.е.
,
т.е.
 можно ввести только 2 новые переменные
х4
и х5:
можно ввести только 2 новые переменные
х4
и х5:
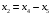 и
и
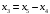 .
.
Тогда целевая функция будет иметь вид:
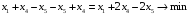
Ограничение
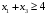 заменится на
заменится на
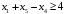 .
.
Записываем для этой задачи канонические формы:
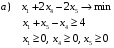
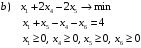
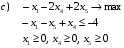
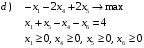
Задача 1.2.1
Докажите лемму 1, следствие из нее и признак оптимальности в краткой форме:
Лемма
1.
При любых
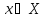 и
и
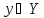 выполняется
неравенство
выполняется
неравенство
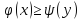
Важным является прямое следствие этой леммы, которое позволяет сформулировать и признак оптимальности в самой простой форме.
Следствие.
Если 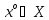 и
и
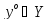 таковы, что
таковы, что
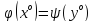 ,
,
то х° — оптимальный вектор в исходной задаче, а у° — в двойственной.
Доказательство.
Введем вектор
переменных прямой задачи
 и вектор переменных двойственной задачи
и вектор переменных двойственной задачи
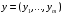 .
.
Записываем прямую задачу:
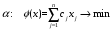 – целевая функция
прямой задачи;
– целевая функция
прямой задачи;
все ограничения
запишем в виде неравенств:
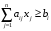 ,
i
=1,2,…m.
,
i
=1,2,…m.
Записываем двойственную задачу:
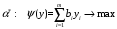 – целевая функция
двойственной задачи;
– целевая функция
двойственной задачи;
все ограничения
запишем в виде неравенств:
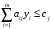 ,
j
=1,2,…n.
,
j
=1,2,…n.
Умножим каждое
i-тое
неравенство системы ограничений прямой
задачи
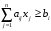 на
переменную yi
и сложим правые и левые части полученных
неравенств.
на
переменную yi
и сложим правые и левые части полученных
неравенств.
Получим:
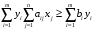 .
.
Аналогично, умножим
каждое j-тое
неравенство системы ограничений
двойственной задачи
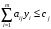 на переменную xj
и сложим правые и левые части полученных
неравенств.
на переменную xj
и сложим правые и левые части полученных
неравенств.
Получим:
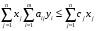 .
.
Левые части
неравенств представляют собой одно и
то же выражение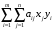 .
.
Поэтому можно
записать двойное неравенство:
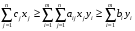 .
.
Т.к.
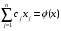 и
и
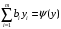 ,
получаем требуемое неравенство:
,
получаем требуемое неравенство: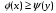 .
.
Следствие из
леммы 1. Если
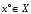 и
и
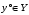 таковы, что
таковы, что
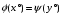 ,
то х°
– оптимальный вектор в исходной задаче,
а у°
– в двойственной.
,
то х°
– оптимальный вектор в исходной задаче,
а у°
– в двойственной.
Доказательство:
Согласно доказанной
лемме 1 при любых допустимых решениях
прямой и двойственной задачи
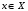 и
и
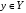 выполняется неравенство
выполняется неравенство
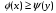 .
.
Т.к. для векторов
х° и
у° выполняется
равенство
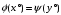 ,
то х°
– вектор в исходной задаче, при котором
достигается наименьшее значение функции
,
то х°
– вектор в исходной задаче, при котором
достигается наименьшее значение функции
 ,
а у°
– вектор в двойственной задаче, при
котором достигается наибольшее значение
функции
,
а у°
– вектор в двойственной задаче, при
котором достигается наибольшее значение
функции
 .
Следовательно, х°
– оптимальный вектор в исходной задаче,
а у°
– в двойственной.
.
Следовательно, х°
– оптимальный вектор в исходной задаче,
а у°
– в двойственной.
Признак
оптимальности
(в краткой форме). Для оптимальности в
прямой задаче допустимого вектора
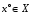 достаточно, чтобы нашелся допустимый
вектор в двойственной задаче
достаточно, чтобы нашелся допустимый
вектор в двойственной задаче
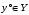 такой, что
такой, что
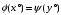 .
.
Доказательство.
Пусть существует
допустимый вектор в двойственной задаче
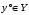 такой, что
такой, что
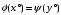 .
Тогда для любого допустимого вектора
.
Тогда для любого допустимого вектора
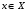 прямой
задачи на основании леммы 1 выполняется
неравенство
прямой
задачи на основании леммы 1 выполняется
неравенство
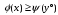 .
Т.к. для вектора
.
Т.к. для вектора
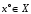 по
условию выполняется равенство
по
условию выполняется равенство
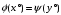 ,
то получаем, что
,
то получаем, что
 .
.
Следовательно,
значение целевой функции на любом
допустимом векторе
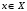 прямой
задачи больше или равно значению целевой
функции на векторе
прямой
задачи больше или равно значению целевой
функции на векторе
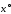 ,
т.е. на векторе
,
т.е. на векторе
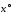 значение целевой функции минимально.
Отсюда следует, что вектор х°
– оптимальный вектор в прямой задаче.
значение целевой функции минимально.
Отсюда следует, что вектор х°
– оптимальный вектор в прямой задаче.
