Задача 1.4.1

Для следующих задач линейного программирования запишите двойственные к ним и найдите оптимальные решения:

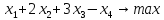
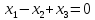
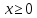
Решение:

Прямая задача:

Записываем двойственную задачу как задачу минимизации. Число переменных в двойственной задаче равно числу ограничений в прямой задаче, т.е. равно двум. Т.к. все ограничения прямой задачи являются равенствами, то переменные y₁ и y₂ двойственной задачи могут быть любыми числами.

Т.к. переменные прямой задачи х_i ≥ 0, то все условия системы ограничений двойственной задачи на минимум будут неравенствами вида ≥.

Двойственная задача:

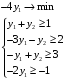
y₁ и y₂ – любые числа.

Решаем двойственную задачу.

Составим и решим систему из первых двух уравнений:

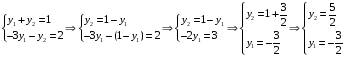
Проверяем выполнение всех остальных ограничений двойственной задачи при полученных значениях 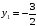и .

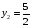Третье ограничение: 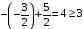– выполняется;

четвёртое ограничение: 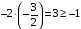– выполняется.

Т.к. все неравенства выполняются, то выполняются условия достаточного признака оптимальности и вектор 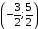даёт оптимальное решение двойственной задачи. Минимальное значение целевой функции на этом векторе равно .

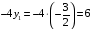Находим решение прямой задачи, используя теорему двойственности, согласно которой ненулевым компонентам оптимального решения одной из взаимно-двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи.

Т.к. первые два неравенства в двойственной задаче выполняются как равенства, переменные x₁ и x₂ в оптимальном решении прямой задаче будут ненулевыми. А т.к. последние 2 ограничения в двойственной задаче выполняются как строгие неравенства, переменные x₃ и x₄ в оптимальном решении прямой задаче будут нулевыми.

Находим решение системы ограничений прямой задачи при x₃ =0 и x₄=0:

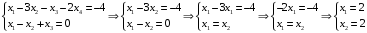
Следовательно, оптимальное решение прямой задачи достигается при x₁ =2, x₂=2, x₃ =0 и x₄=0. Максимум целевой функции прямой задачи также равен 6:

.

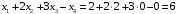Задача 1.4.2

Для следующих задач линейного программирования найдите оптимальные решения в зависимости от указанных параметров (величины некоторых ограничений) и проведите исследование изменения оптимального решения и оптимального значения целевой функции при изменении параметра:

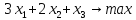
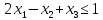
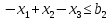
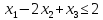
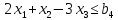
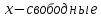
 Решение:

Записываем двойственную задачу. Т.к. x – свободные переменные, ограничения в двойственной задаче будут в виде равенств, а т.к. все ограничения прямой задачи заданы в виде неравенств, то двойственные переменные должны быть неотрицательными.

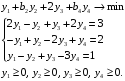
Решаем систему трёх уравнений с 4-мя неизвестными:

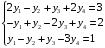
Т.к. , ранг системы равен 3.

Пусть y₄ будет свободной переменной. Выражаем переменные y₁, y₂ и y₃ через переменную y₄:

.

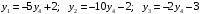По условию данной двойственной задачи все двойственные переменные должны быть неотрицательными, но видим, что при 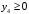переменные y₂ и y₄ получаются отрицательными. Следовательно, оптимального решения двойственная задача не имеет при любых значениях параметров b₂ и b₄. Отсюда следует, что целевая функция прямой задачи при любых значениях параметров b₂ и b₄ не ограничена.

Задача 1.4.3

Для следующих содержательных постановок постройте математическую модель в виде задачи линейного программирования, приведите ее к какой-либо известной вам канонической форме, сформулируйте двойственную задачу и условия признака оптимальности, найдите решения пары двойственных задач, проинтерпретируйте двойственные оценки:

Нефтеперерабатывающий завод производит за месяц 1 500 000 л.алкилата, 1 200 000 л.крекинг-бензина и 1 300 000 л.изопентола. В результате смешивания этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сортов А и Б, соответственно. Стоимость 1000 л. бензина сорта А и Б, соответственно, равна 90 и 120 ед. Определить месячный план производства бензина сорта А и Б, максимизирующий стоимость выпущенной продукции.

Решение:

Обозначим

x₁ – Решение:

Обозначим

x₁ – месячный план производства бензина сорта А в тыс. л,

x₂ – месячный план производства бензина сорта Б в тыс. л.

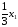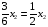Алкилата в x₁ тыс. л произведённого бензина сорта А будет присутствовать л, а в x₂ тыс. л бензина сорта Б л;

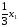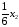крекинг-бензина в x₁ тыс. л произведённого бензина сорта А будет присутствовать л, а в x₂ тыс. л бензина сорта Б л;

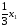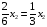изопентола в x₁ тыс. л произведённого бензина сорта А будет присутствовать л, а в x₂ тыс. л бензина сорта Б л.

По условию задачи нефтеперерабатывающий завод производит за месяц 1 500 тыс. л алкилата, 1 200 тыс. л крекинг-бензина и 1 300 тыс. л изопентола.

Следовательно, имеем следующие ограничения на имеющиеся ресурсы:

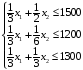или

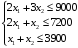
Стоимость выпущенной продукции составит 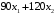. Эту величину надо сделать максимальной.

Следовательно, математическая модель задачи имеет вид:

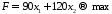(стоимость бензина)

при следующих ограничениях на потребление компонентов в течение месяца:

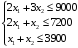
и при выполнении условий неотрицательности переменных:

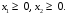
В таком виде задача приведена к канонической форме 1 задачи на максимум.

Решаем задачу геометрически.

Имеем пятиугольник допустимых решений ABCOD и вектор 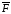направления возрастания целевой функции. Координаты вектора 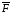пропорциональны коэффициентам целевой функции.

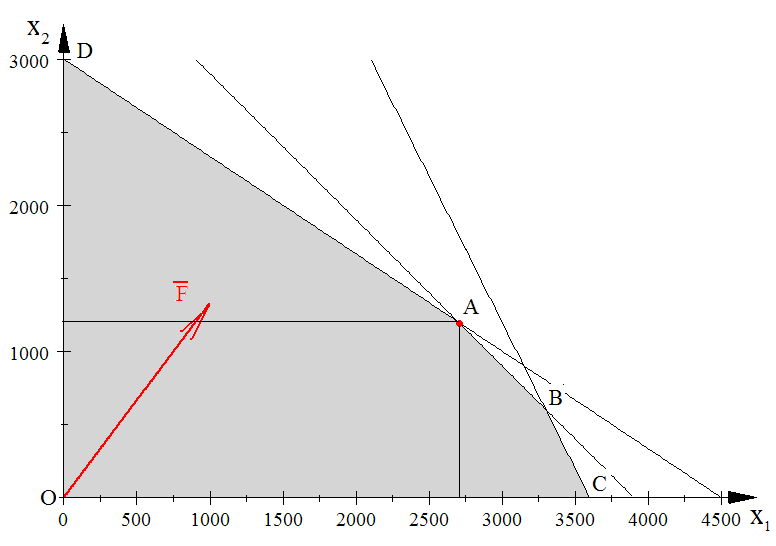
Максимум достигается в точке А пересечения прямых и .

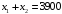Находим координаты этой точки, решая систему уравнений:

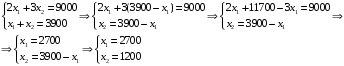
Следовательно, оптимальный месячный план производства бензина сорта А и Б, максимизирующий стоимость выпущенной продукции, следующий:

выпускать 2700 тыс. л бензина сорта А и 1200 тыс. л бензина сорта Б.

При этом стоимость выпущенного бензина будет максимальна и равна

усл. ед.

Двойственная задача является задачей на минимум, имеет 3 неотрицательные переменные и 2 ограничения вида ≥ :

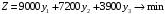
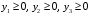
Условия признака оптимальности:

Положительным (ненулевым) компонентам оптимального решения одной из взаимно-двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи.

Должны выполняться следующие равенства:

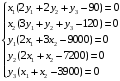
Подставляем в эти уравнения известное решение прямой задачи х₁=2700, х₂=1200 и получаем систему уравнений для определения y₁, y₂, y₃:

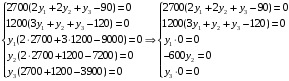
Из 4-го уравнения получаем, что y₂=0. Тогда система получает следующий вид:

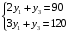
Решение этой системы: .

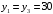Следовательно, оптимальное решение двойственной задачи: y₁=30, y₂=0, y₃=30.

Двойственные оценки y₁=30 и y₃=30 показывают, что если увеличить производство алкилата или изопентола на 1 тыс. л в месяц, то стоимость выпущенного бензина в том и в другом случае возрастёт на 30 усл. ед.

Двойственная оценка y₂=0 показывает, что при увеличении производства крекинг-бензина стоимость выпущенного бензина не изменится, т.к. крекинг-бензин не является дефицитным ресурсом и при оптимальном плане расходуется не полностью, 600 тыс. л каждый месяц остаётся неиспользованным.