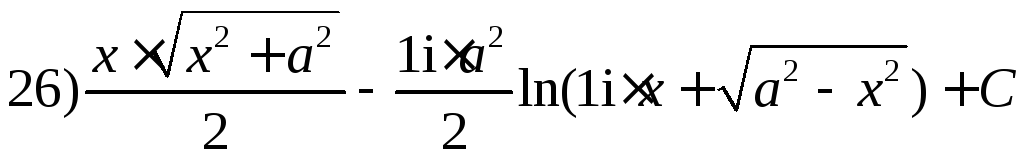1-й курс, 2-й семестр.

Неопределённый интеграл

1) Понятие о первообразной и неопределённом интеграле.

Теорема об общем виде первообразной.

Определение: первообразная F(x) для функции f(x)-функция, такая, что F’(x)=f(x) (1). Не всякая элементарная функция имеет первообразную среди элементарных функций. Общий вид первообразной называется неопределённым интегралом. Пусть F’(x)=f(x) (F(x)+C)’=f(x) еслиF(x)является первообразной функции f(x), то F(x)+C также является первообразной функции f(x).

Теорема об общем виде первообразной:

Любая первообразная функции f(x) имеет вид F(x)+C, где F(x)-фиксированная первообразная, а С - постоянная.

Доказательство:

Пусть имеется две первообразных для функции f(x): F(x) и F₁(x). Рассмотрим их разность (F(x) - F₁(x)) и продифференцируем её:

(F(x) - F₁(x))’=f(x)-f₁(x)=0

F(x)-F₁(x)=φ(x)₁(φ(x))’=0φ(x)=C

(2) – обозначение для неопределённого интеграла (общая форма)

2) Свойства неопределённых интегралов:

а) б)

в) г)д)е)

ё)

Таблица первообразных

Функция	Первообразная

Примеры:

Замена переменной в интеграле:

Интегрирование по частям.

Интегрирование рациональной дроби.

1) Вывод формулы

2)Типы функций, интегрируемые по частям.

а) 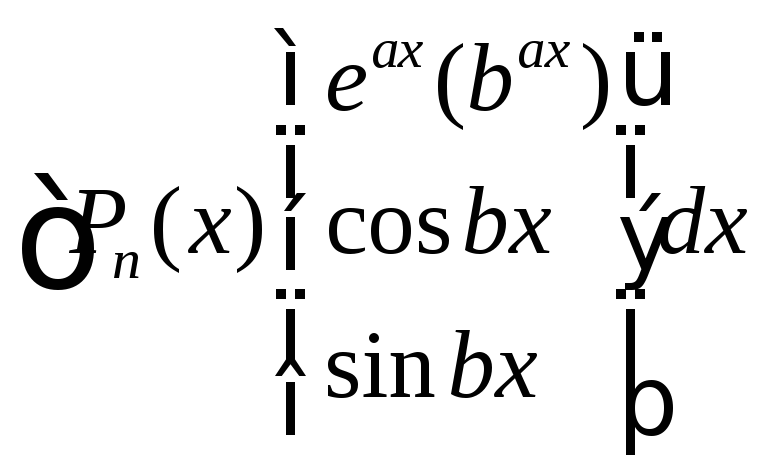P_n(х)-многочлен степени n.

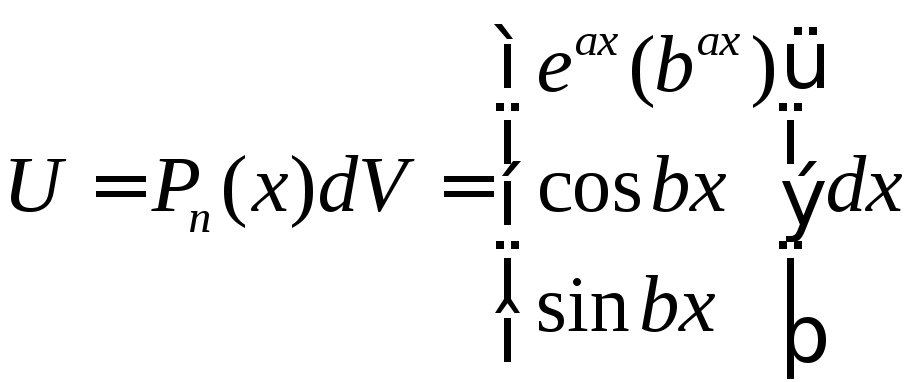
б)

R_n-рациональная, иррациональная

R_n,Q-некоторые функции от Х.

в) Циклические интегралы

К циклическим интегралам относятся интегралы специального вида:

Примеры:

Интегрирование рациональных дробей

1) Интегрирование простейших рациональных дробей

Рациональной дробью называется отношение двух многочленов , гдеn-степень числителя, а m-знаменателя. По теореме Безу, знаменатель этой дроби можно разложить в произведение множителей:

Если дробь числителя n больше степени знаменателя m, то такая дробь называется неправильной.

Если дробь неправильная, то либо делением «уголком», либо вспомогательными процедурами из неё выделяется правильная часть

Четыре типа простейших правильных дробей:

1)

2)

3)

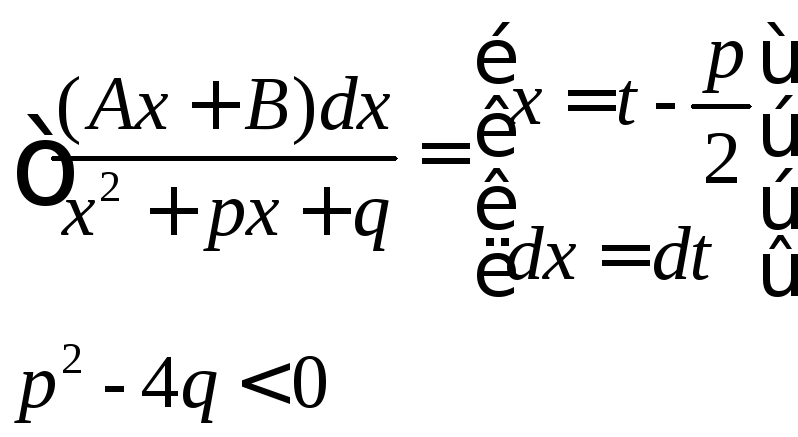
ПРИМЕР:

4).Используется подстановка

2) Интегрирование рациональных дробей, содержащих многочлен:

Дана дробь.P и Q – многочлены вида:

Каждому из сомножителей соответствуют дроби:

Дроби данного вида интегрируются по следующему алгоритму:

1) По виду знаменателя находим разложение на простейшие дроби

2) Суммируем эти простейшие дроби

3) Приводим их к общему знаменателю

4) Находим неопределенные коэффициенты (А₁,А₂,…)

5) Интегрируем полученную сумму

Пример №1

Находим неопределенные коэффициенты:

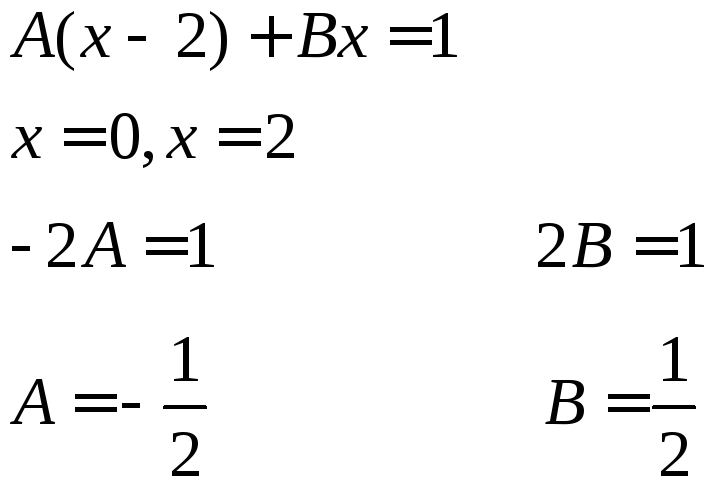
Получили разложение исходной дроби:

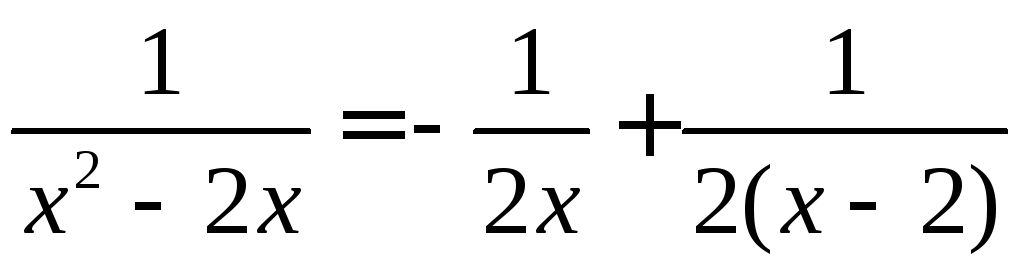
Пример №2:

Записываем исходную дробь в виде суммы дробей с неопределенными коэффициентами:

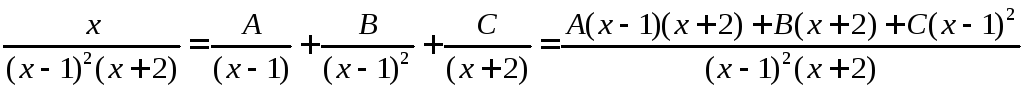Определяем неизвестные коэффициенты:

Сравниваем коэффициенты при х²:

Пример №3:

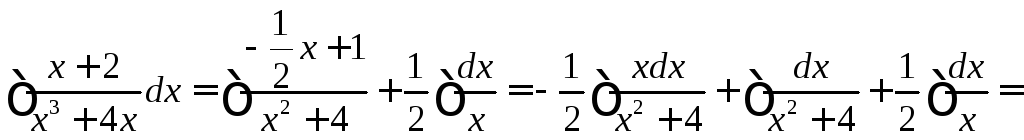
Приравниваем коэффициенты при равных степенях:

Х²:

Х:

1:

Интегрирование тригонометрических выражений

Вид интегрируемого выражения: .

R- рациональная функция от sin x и cos x

Способы интегрирования данных выражений:

Если R(-sin x, cos x)= -R(sin x, cos x), тогда делается замена t=cos x

Если R(sin x, -cos x)= -R(sin x, cos x), тогда делается замена t=sin x

Если оба нечетны, то делается замена для наибольшей степени

Если R(-sin x, -cos x)= -R(sin x, cos x), тогда делается замена t=tg x

Используется также универсальная тригонометрическая подстановка , при этом разрыв тангенсане должен попасть на область интегрирования – это существенно для определенных интегралов.

Некоторые формулы, полезные в интегрировании тригонометрических выражений:

ПРИМЕРЫ:

№1

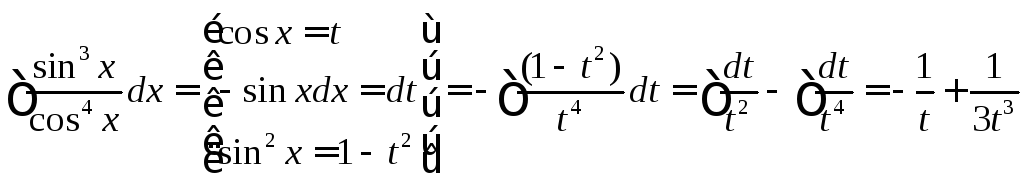
№2

Интегрирование иррациональных выражений

Вид интегрируемого выражения:.

В этом интеграле производится замена ax+b=t^s, где s-НОК(k_1,k₂) (наименьшее общее кратное чисел k_1,k₂)

ПРИМЕР:

Интегрирование иррациональных выражений, содержащих квадратный трехчлен.

Виды интегрируемых выражений и подстановки, служащие для их упрощения:

ПРИМЕР:

Найдем длину дуги четверти астроиды:

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Задача о площади криволинейной трапеции

Рассмотрим криволинейную трапецию ABCD (рис. 1). Разделим основание АВ данной фигуры произвольным образом на части и проведем ординаты. Соответствующие точкам деления. Тогда криволинейная трапеция разобьется на ряд полосок (см. рис. 1). Заменим теперь приближенно каждую полоску некоторым прямоугольником, основание которого то же, что и у полоски, а высота совпадает с одной из ординат полоски, скажем, крайней слева. Таким образом, криволинейная фигура заменится некоторой ступенчатой фигурой, составленной из отдельных прямоугольников.

Обозначим точки деления:

. (22)

Основание -го прямоугольника, очевидно, равно разности, которая обозначена через. Высота, следовательно, равна, поэтому площадь-го прямоугольника равна.

Просуммировав площади всех прямоугольников, получим приближенное значение площади криволинейной трапеции:

.

Погрешность этого равенства при безграничном убывании всех стремится к нулю.Точное значение площади получится как предел

(23)

в предположении, что все одновременно стремятся к нулю. Для предельного значения суммы (23) введено обозначение- в случае площади фиксированной фигурыABCD, отвечающей изменению отдо.

Понятие определенного интеграла

Пусть определена на отрезке. Разделим отрезокнапроизвольных частей точками, выберем на каждом элементарном отрезкепроизвольную точкуи найдем длину каждого такого отрезка:.

Интегральной суммой для функции на отрезкеназывается сумма вида (рис. 2):

(24)

Определенным интегралом от функции на отрезке(в пределах отдо) называется предел интегральной суммы (24) при условии, что длина наибольшего из элементарных отрезковстремится к нулю:

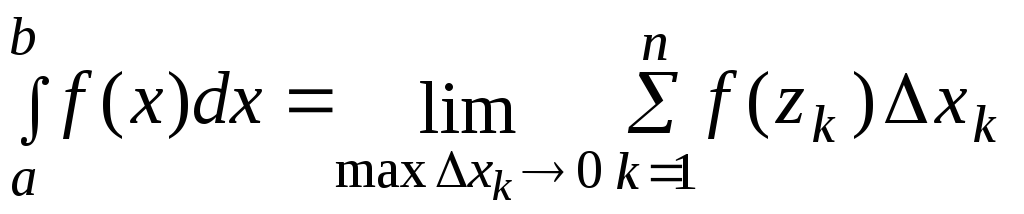. (25)

Если для функции , заданной на, предел (25) существует и не зависит как от способа разбиения отрезкана элементарные, так и выбора точек, то говорят, что функцияинтегрируема на .

Теорема о существовании определенного интеграла. Если функция непрерывна на , то она интегрируема на.

Отметим, что в отличие от неопределенного интеграла, определенный интеграл для фиксированных значений и-число.

Основные свойства определенного интеграла

1) .

2) .

3) .

4) .

5) .

6) Оценка определенного интеграла: если на, то.

7) Если четная функция, то.

8) Если нечетная функция, то.

Определенный интеграл как функция верхнего предела

Если функция интегрируема в промежуткето она интегрируема и в промежутке, где- любое значение из. Рассмотрим функцию

(26)

Эта функция обладает следующими свойствами:

1. если функция непрерывна на, тобудет непрерывной на том же промежутке;

2. если функция непрерывна на, то в любой точкефункцияимеет производную, равную:.

Таким образом, функция , определенная равенством (26), являетсяодной из первообразных функции на.

Вычисление определенного интеграла с помощью формулы Ньютона-Лейбница.

Пусть функция непрерывна на , а- одна изнепрерывных на , первообразных для, т.е. , тогда справедлива формула Ньютона-Лейбница:

. (27)

Таким образом, чтобы вычислить определенный интеграл по данной формуле, необходимо: 1) проверить, что непрерывна на ; 2) найти первообразную подынтегральной функции , проверить ее на непрерывность на и только потом воспользоваться формулой Ньютона-Лейбница.