6. Чертежи перспективы

Чертежом перспективы (иногда просто перспективой) называют об-

ратимый чертёж, состоящий из двух проекций, которые получены методом центрального проецирования.

Чертежи перспективы широко применяются архитекторами в ходе архитектурного проектирования. При этом на изображения перспективы накладываются некоторые ограничения, о которых мы скажем ниже. Перспектива, как и фотография, обладает особой наглядностью. Она хорошо выявляет трёхмерность объёмных объектов, глубинность пространства, позволяет передавать пространственный характер окружающей среды и отражает взаимное положение наблюдателя и объекта. При этом она передаёт кажущиеся изменения величины и формы объекта в зависимости от положения объекта и наблюдателя. Перспектива, как и любой чертёж, позволяет получить изображение ещё не существующего, проектируемого инженерного объекта. При этом получение перспективы гораздо дешевле и проще, чем получение макета проектируемого объекта.

6.1. Геометрическая схема построения чертежа перспективы

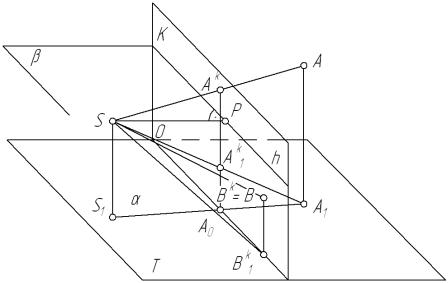
Основой схемы является плоскость проекций и центр проецировани ы. Обозначим эту плоскость буквой К, рис. 81. Точка S К − центр проецирования. Существует традиция располагать оригиналы за картиной по отношению к точке S. Это пространство назовём предметным.

Пусть в предметном пространстве имеется точка С (рис. 81). Покажем центральную проекцию этой точки на плоскость К . Для этого прове-

Рис. 81

85

дём через центр проецирования S проецирующую прямую в точку С. Остаётся решить задачу пересечения проецирующей прямой с ка ртиной. Мы умеем решать эту задачу, но только на полном чертеже. На рис. 81 чертёж неполный, т. к. и точка S , и точка С имеют по одной проекции на чертеже. Воспользуемся рис. 81 как иллюстрацией. Тогда проекцию С к точки С на плоскости К можно обозначить где угодно на луче SC. Пусть далее в предметном пространстве имеется прямая L, пересекающая плоскость К в точке А. Проведя проецирующую прямую в точку А, мы получим А к = А. Это вполне естественно. Для получения проекции Lк необходимо получить проекцию на К ещё одной точки, принадлежащей L. Проводя проецирующие прямые в различные точки прямой L, мы можем получать проекции её точек. Проведем проецирующую прямую, параллельную L. Следует ожидать, что мы не получим никакой точки на картине. Однако это не так. Проецирующая прямая, параллельная L, пересекает К, т. к. сама L ∩ К = А. Но параллельные прямые не пересекаются. Так мы учили в школьной геометрии Евклида. Этот парадокс был разрешён французским геометром Понселе. Он решил, что параллельные прямые также пересекаются, но в бесконечно удалённой точке. Таким образом две прямые могут пересекаться либо в обычной, либо в бесконечно удалённой точке. Кроме того, две прямые, конечно, могут вообще не иметь общих точек, то есть скрещиваться.

Дополнение прямых бесконечно удалёнными точками повлекло за собой появление некоторых бесконечно удалённых фигур. Так, множество бесконечно удалённых точек прямых, лежащих в одной плоскости приводит к тому, что в плоскости п оявляется бесконечно удалённая линия, на которой лежат все эти точки. Удобно считать, что эта линия будет бесконечно удалённой прямой. Итак получается, что две плоскости, параллельные друг другу, пересекаются по бесконечно удалённой прямой.

Наконец, естественно предполагать, что всё трёхмерное пространство имеет бесконечно удалённую плоскость, которая содержит все бесконечно удалённые фигуры. Эту плоскость можно «увидеть », посмотрев на голубое солнечное бездонное небо. Бесконечно удалённые фигуры короче называют «несобственными» фигурами. Пространство, обогащённое не-

собственными фигурами, называют расширенным евклидовым простран-

ством. Геометрию этого пространства можно построить, вводя некоторые аксиомы. Это приводит к новой геометрии, называемой «проективной геометрией». Вот, оказывается, что кроется в такой простой операции как центральное проецирование.

∞

Возвратимся к рис. 81. Теперь мы можем считать Е к проекцией

∞

бесконечно удалённой точки Е прямой L. Полезно запомнить, что для п о-

86

лучения несобственной точки прямой необходимо провести проецирую-

∞

щую прямую, параллельную этой прямой. Точка Е к называется точкой схода перспектив прямых L и L', параллельных в пространстве заданному направлению. Таких прямых будет бесчисленное множество. Как уже говорилось, чертёж прямых, полученных на рис. 81, не является полным, т. к. каждая прямая, либо точка имеют в этой геометрической схеме только одну проекцию. Полный чертёж, как нам известно, состоит как минимум из двух проекций.

Рис. 82

На рис. 82 показана геометрическая схема, дополненная плоско-

стью Т К . Линия пересечения плоскостей Т и К называется основанием картины. Плоскость Т называется предметной плоскостью. Пусть в пре д- метном пространстве имеется точка А . Получим её полный чертёж на плоскости К с помощью центрального проецирования из центра S. Дополним чертеж ортогональными проекциями точек S и А на предметную плоскость. Основание соответствующих перпендикуляров S1 и A1 назовём основаниями соответствующих точек. Так A1 − основание точки А, S1 − основание точки S. Последнюю иногда называют «точкой стояния» или «точкой зрения» (термин из компьютерной графики). Это происходит из того, что оказывается модель пространства, придуманная Понселе, является моделью нашего зрения (мы видим идущие от нас параллельные прямые сходящимися). Поэтому можно считать прямую SS1 позицией наблюдателя, который наблюдает через прозрачную плоскость картины предметное пространство.

Возвращаясь к нашей геометрической схеме (рис. 82), мы убеждаемся в полноте этого чертежа (точки S и А имеют две проекции). Теперь на

87

этом чертеже можно решать позиционные задачи. Построим чертёж перспективы точки А на картине К. Проведем прямую SA (посмотрим на точку А с позиции S) и определим точку пересечения SA с плоскостью картины. Проведём плоскость-посредник α Т через проецирующую прямую SA. Эта плоскость пересекает плоскость Т по прямой S1 , A1 , а плоскость К по прямой, перпендикулярной основанию картины и проходящей через точку А0 , лежащую на основании картины. Последняя прямая пересекает прямую SA в точке А к, которая является перспективой точки А на плоскости К. Однако чертёж точки А в плоскости картины не является полным. Поэтому проецируем на К основание A1 . Чертеж, состоящий из перспективы А к точки А и перспективы А к1 той же точки, является полным чертежом перспективы точки А. Для любой фигуры условия полноты перспективного чертежа будут такими же.

Анализируя рис. 82, можно представить себе особенности чертежа перспективы точки, различно расположенной в пространстве.

Очевидно, что точки, лежащие в картинной плоскости, имеют перспективу основания на основании картины (см. чертёж точки В К на рис. 82). При удал ении точки от плоскости картины перспектива основания точки удаляется от основания картины по прямой, перпендикулярной основанию картины. Естественно задать вопрос: где будет располагаться перспектива основания бесконечно удалённой от картины точки? Ответ очевиден: она будет располагаться на бесконечно удалённой прямой предметной плоскости Т. Чтобы обнаружить эту точку надо провести через S проецирующую прямую, параллельную плоскости Т. Таких прямых мн о-

жество. Все они лежат в плоскости β, параллельной плоскости Т , которая пересекает плоскость К по прямой h, параллельной основанию картины. Одна из прямых, лежащих в плоскости β и проходящих через точку S, будет перпендикулярна К и, следовательно, h. Точка пересечения Р этой прямой с картиной называется главной точкой картины, а отрезок SР называется главным лучом картины. Линия h является перспективой бесконечно удалённой прямой предметной плоскости Т. Теперь ясно, что основания перспектив бесконечно удалённых от картины точек пространства будут располагаться на прямой h, которая называется линией горизонта (это название знакомо нам из нашей зрительной практики).

Исходя из приведенных рассуждений, можно читать чертежи точек, различно расположенных в предметном пространстве.

Рассмотрим рис. 83. Здесь изображены перспективы точек А, В, С, D, Е, К. Установить положение точки по чертежу перспективы проще всего, рассматривая положение на чертеже перспективы основания точки. Так, точка

88

зонта h . Точка В расположена на некотором конечном расстоянии от картинной плоскости поскольку В к1 не совпадает с основанием картины.

Рис. 83

Отрезок В к1 В к моделирует расстояние от точки В до предметной плоскости. Точка К лежит в предметной плоскости Т поскольку К к = К к1 . Точка Е является бесконечно удаленной от картины точкой, т. к. Е к1 лежит на линии горизонта. Точка Е располагается выше плоскости β на бесконечно удаленной плоскости предметного пространства. Рассмотрим теперь точки С и D. Перспективы этих точек совпадают: С к = D к. Но тогда эти точки л е- жат на одной и той же проецирующей прямой и являются конкурирующими по отношению к плоскости картины. Возникает вопрос о видимости точек на чертеже перспективы. Очевидно, что будет видна точка D, заданная перспективой D к , поскольку D к1 располагается ближе к основанию карти-

ны, чем С к1 .

Процесс чтения чертежей перспектив точек очень важно освоить, т. к. он лежит в основе процесса чтения чертежей перспектив более сложных фигур.

Рассмотрим простейшие операции с чертежами перспектив прямых. Прямую можно задать двумя принадлежащими ей точками. На рис. 84, а отрезок прямой задан точками А и В. Соединяя одноименные проекции этих точек, мы получаем перспективу отрезка и перспективу основания отрезка. Продолжая перспективу основания до пересечения с основанием картины, получим точку N k1 .

89

На вертикальной линии связи получим точку N k, которая является перспективой точки пересечения прямой АВ с картинной плоскостью. Эта точка называется картинным следом прямой. Если теперь продлить перспективу основания А к1 В к1 прямой АВ до пересечения с линией горизонта, то полу-

∞

Точка Ек будет перспективой точки пересечения прямой АВ с несобственной плоскостью предметного пространства. Эта точка называется несобственным следом прямой (в ней сходятся перспективы всех прямых, параллельных АВ ). Поэтому она называется также точкой схода. На рис. 84, б прямая a задана проекциями a к и a к1 . Точка пересечения проекций М к = М к1 является следом прямой a на предметной плоскости Т, предметным следом прямой. Наконец, на чертеже рис. 84, в задана горизон-

∞

тальная прямая b своими проекциями b k , b k1 . Точка схода Е этой прямой

∞ ∞

будет лежать на линии горизонта: Ек= Ек1 .

Таким образом, мы установили, что прямая общего положения может в геометрической схеме построения перспективы иметь картинный, предметный и несобственный следы. Любые два из этих следов могут задавать прямую.

90

параллельна основанию картины. Точка М С является предметным следом прямой С. Прямые d и l (рис. 85, б) параллельны друг другу и имеют точку схода в главной точке картины (точка Р ). Исходя из этого, прямые перпендикулярны картине (параллельны главному лучу, см. рис. 82). Прямая l (рис. 85, в), очевидно, параллельна и картинной, и предметной плоскостям. Прямая АВ (рис. 85, г) перпендикулярна предметной и параллельна картинной плоскости. Построим через точку А прямой АВ горизонтальную

ной прямой, можем совместить прямую АВ с картиной и таким образом получить истинную длину отрезка АВ. Таким образом можно решать задачу построения истинной величины отрезка прямой только в случае, когда прямая в предметном пространстве расположена параллельно картине. Это происходит потому, что параллельные между собой прямые в предметном пространстве сохраняют параллельность и в перспективе, если они к тому же параллельны и картинной плоскости.

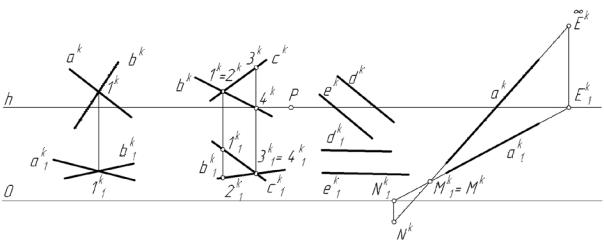
На рис. 86 показаны чертежи двух прямых, различно расположенных в пространстве. Прокомментируем их в порядке слева направо.

На рис. 86, а показан чертеж перспективы двух взаимно пересекающихся прямых a и b . Из чертежа видно, что перспективы прямых и перспективы оснований прямых пересекаются в единственной точке 1 (1 k, 1 k1 ).

91

На рис. 86, б показан чертеж перспективы скрещивающихся прямых b и с. Как видно из чертежа, точки пересечения перспектив прямых и их оснований перспектив являются конкурирующими точками 1, 2 и 3, 4.

На рис. 86, в показаны чертежи перспектив двух взаимно параллельных в предметном пространстве прямых d и e, которые к тому же параллельны плоскости картины. Перспективы этих прямых и основания перспектив у них сохраняют параллельность.

На рис. 86, г показан чертеж перспективы произвольно расположенной прямой a и построены её следы: М – на предметной плоскости, N – на

∞

картинной, Е – на несобственной.

На рис. 87 показаны чертежи перспектив плоскостей частного положения в предметном пространстве. На рис. 87, а плоскость α задана пересекающимися в точке 1 прямыми a и b. Построив точки схода этих пря-

∞ ∞

мых, убеждаемся, что эти точки F и F ′ располагаются на линии горизонта. Но тогда эти линии параллельны предметной плоскости, т. е. являются горизонталями. Отсюда ясно, что плоскость α является горизонтальной плоскостью. Это подтверждается положением картинных следов прямых a и b. Эти следы N k и N ′ k находятся на прямой, параллельной линии горизонта. Но эта прямая αK является картинным следом плоскости α. След плоскости α на предметной плоскости является несобственной прямой αТ, сов-

∞

падающей с линией горизонта, которая является перспективой αЕ этой

∞

прямой на картинной плоскости. Прямая αЕ (следовательно, и линия горизонта) является линией схода всех горизонтальных плоскостей.

92

предметной плоскости. Из чертежа видно, что основания перспектив всех точек, лежащих в плоскости β (следовательно, и любых других фигур, принадлежащих плоскости β ) лежат на предметном следе βТ этой плоскости. Для плоскости β построены картинный след β к и след на несобствен-

∞

ной плоскости βЕ. Последний параллелен следу β к и является линией схода плоскостей, перпендикулярных предметной плоскости, проходящих че-

∞

рез этот след. Добавим, что поскольку след βЕпроходит здесь через главную точку Р картины, плоскость β перпендикулярна также несобственной плоскости.

На чертеже рис. 88 двумя взаимно пересекающимися прямыми a и b задан чертеж перспективы плоскости α общего положения. Требуется построить следы плоскости на предметной, картинной и несобственной плоскостях. Как мы отметили ранее, следы плоскости проходят через соответствующие следы прямых, лежащих в этой плоскости. Построим следы прямых a и b на предметной плоскости Т. Эти следы МaТ и МbТ находятся как точки пересечения перспектив прямых a и b с перспективами их оснований. След αТ плоскости α проходит через эти точки.

93

Рис. 88

фронтали горизонтальная проекция параллельна основанию картины. Приведённые нами задачи были позиционными. Для решения мет-

рических задач на чертеже перспективы схему, показанную на чертеже рис. 82, необходимо дополнить элементами системы параметризации геометрических фигур, изображаемых в перспективе. Рассмотрим введение системы параметризации в схеме, показанной на рис. 82. Наиболее просто и естественно расположить две оси координат в плоскости картины. Тем самым плоскость К становится координатной плоскостью. Пусть, например, ось абсцисс совпадает с основанием картины, а ось аппликат пересекает её под прямым углом. Тогда ось ординат будет перпендикулярна плоскости К и, следовательно, будет иметь точку схода в главной точке картины. В этих рассуждениях остаётся неопределённым вопрос о том, как производить измерения отрезков по оси 0у - оси ординат. Измерения по

94