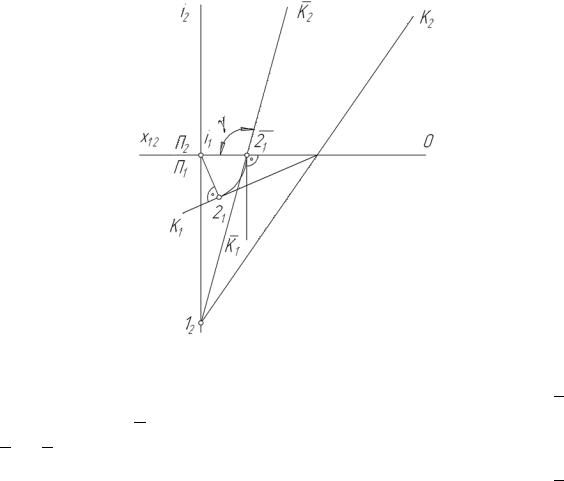
Пусть теперь картинная плоскость занимает общее положение в схеме построения перспективы. Тогда задача усложняется.

Приведём решение вспомогательных задач по определению элементов геометрических схем построения чертежей перспективы на наклонной картинной плоскости общего положения. Как видно из рис. 106, необходимо знать истинную величину угла наклона плоскости картины к предметной плоскости. Это угол γ. Используется также угол β = 180 о - γ.

Пусть картина задана следами К1 и К2 на плоскостях П1 и П2 . Построение истинной величины угла наклона плоскости К к плоскости П1 может быть получено вращением плоскости К около оси i перпендикулярной плоскости П1 . Ось вращения выбираем расположенной в плоскости П2 , перпендикулярной П1 . Тогда горизонтальная проекция i1 оси − это точка на оси 0х. Из i1 опускаем перпендикуляр на след К1 .

Отрезок i1 , 21 − радиус вращения следа К1 .

Рис. 106

Поворачиваем след К1 до совпадения точки 21 с осью 0X в точке 2 1 . Повернутый след K 1 0X. Новое положение К2 определяется точкой схода 2 1 = 2 2 и оставшейся неподвижной при вращении плоскости точкой 12 .

Искомый угол измеряется между осью 0X и новым положением K 2 − фронтального следа плоскости К, ставшей в новом положении фронтальнопроецирующей.

115

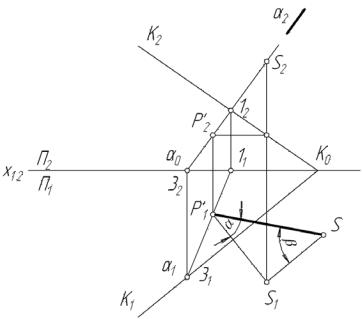
Иногда полезно наряду с углом наклона картины получить положение главной точки и главного луча картины.

Рис. 107

На рис.107 показана картинная плоскость, заданная следами К1 и К2 , а также проекции S1 и S2 центра проецирования S.

Для решения задачи проводим через проекции центра проецирования проекции прямой n, перпендикулярной плоскости К. Эта прямая несёт на себе главный луч картины.

Для построения главной точки Р достаточно найти точку пересечения построенной прямой с плоскостью К. Это сделано с помощью фронтальнопроецирующей плоскости-посредника α, проходящей через прямую n. Проекции Р ′1 и P ′2 являются проекциями главной точки картины. Длину отрезка главного луча можно построить, используя метод прямоугольного треугольника. На чертеже рис. 107 это отрезок SP ′1 .

Кроме того, построен угол β наклона плоскости К к горизонтальной плоскости проекции.

Построения, показанные на чертежах рис. 105-107 используем для решения задачи построения чертежа перспективы на наклонной плоскости по заданным двум ортогональным проекциям объекта (рис. 108).

На исходном чертеже выполнена установка для построения перспективы. Задана плоскость картины К следами К1 и К2 . Заданы проекции центра проецирования S и горизонта h. Задана линия 0 основания картины.

Построены проецирующие прямые в точки 11 , 21 , 31 объекта. Отмечены точки пересечения 10 , 20 , 30 проецирующих прямых с

картиной. Точка 41 находится в картине, отрезок 11 , 21 продолжен до

116

пересечения его с картиной в точке 1 0 . По этой установке можно строить перспективу.

Рис. 108

Для этого в произвольном месте проводим горизонтальную прямую, которую принимаем за основание картины на чертеже перспективы, (рис. 109). Для построения высотных отметок точек необходимо учитывать их изменения в ходе совмещения картины с плоскостью чертежа. Угол наклона к горизонтальной плоскости заданной картины нам известен, это угол γ (рис. 108). Рассматривая рис. 105, можно увидеть, что высотные от-

метки на следе К2 и те же отметки на совмещенном следе K 2 относятся по длине друг с другом как длины гипотенузы и катета в прямоугольном тр е- угольнике. Например, отметка Zh главной точки Р2 является концом гипо-

тенузы в треугольнике Р2 , Р3 , O . Совмещённая отметка является кате-

том Р3 , O в том же треугольнике.

Смоделируем эту ситуацию на рис. 109. В произвольном месте основания картины проводим прямую, перпендикулярную основанию. Принимаем эту прямую за центральную ось картины. В точке РО построенной

главного луча на горизонтальной проекции (рис. 108). Далее, в точке S

117

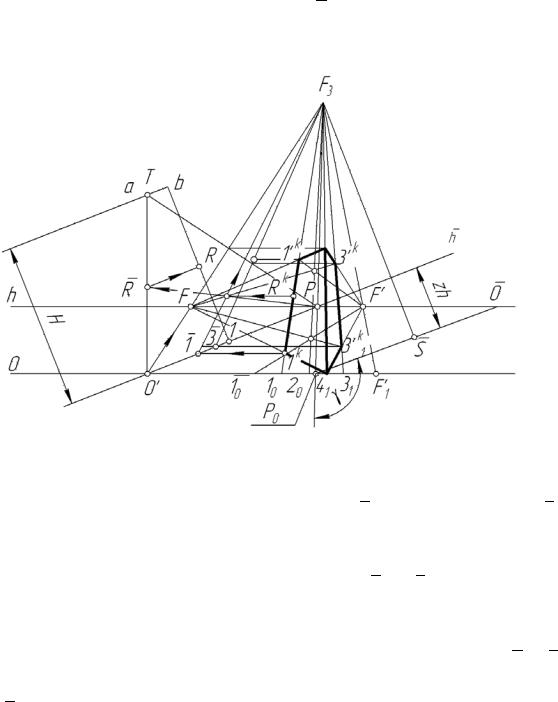
строим прямую, перпендикулярную прямой O , до её пересечения в точке F3 с центральной осью картины. Построенная точка F3 является точкой схода всех вертикальных прямых объекта.

Рис. 109

На расстоянии Zh параллельно прямой O проводим прямую h . Эта прямая пересечет центральную ось в точке Р, которая является совмещённой с плоскостью чертежа главной точкой картины. Легко заметить,

что все измерения, которые мы делали на прямых O и h являются измерениями на картине, не совмещённой с плоскостью чертежа.

Из рис. 109 видно, что высота линии горизонта на чертеже перспек-

тивы, равная отрезку РР0 , относится к расстоянию между прямыми O и h как гипотенуза к катету в треугольнике, аналогичном треугольнику

Р2, Р3 ,O на чертеже рис. 105. Приведенными построениями перспектива полностью задана. Остальные построения, связанные с точками объекта, почти не отличаются от построений перспективы на вертикальной плоскости. Переносим все точки с горизонтального следа картины на установке рис. 108 на основание картины рис. 109. Из точки F ′1 проводим перспективу вертикальной прямой в точку схода F3 . Эта прямая пересекает линию горизонта в точке F ′, которая является точкой схода прямых 1, 2 и 3, 4, а также прямых верхнего основания призмы, параллельных указанным прямым. Аналогичными построениями можно построить и вторую точку схо-

118

да для прямых 1, 4 и 2, 3. В случае недоступности точки схода F можно использовать для построения точек основания призмы другие приёмы. Например, точку 1 К можно построить пересечением вертикальной прямой 10 ,

F3 с прямой 1 O F ′ и т. п. Измерения вертикальных прямых для построения верхнего основания призмы можно выполнить с помощью «вер-

тикальной стены». Для этого на прямой h в любом месте необходимо построить прямые a и b соответственно перпендикулярные прямым О − основанию картины и h .

Эти прямые, также как и прямые O и h ′, моделируют измерения на несовмещенной картине с плоскостью чертежа и совмещённой картине с плоскостью чертежа. Откладываем на прямой b истинную высоту Н вертикального отрезка, взятую с исходного чертежа, и строим на прямой a соответствующую точку Т. Из этой точки проводим прямую в главную точку картины. Поскольку все боковые ребра призмы одинаковы по длине, размер Н пригоден для построения перспектив всех вертикальных рёбер. Для завершения построения «стены» проводим прямую О ′ P пересечения «стены» с предметной плоскостью. Построение перспектив боковых рёбер показано на рис. 109 стрелками. С помощью изложенного приёма можно решать и обратную задачу реконструкции отрезка прямой. На вертикальном ребре 1 К 1 ′ К взята точка R К. Обратными построениями, по-

казанными стрелками, построена точка R на прямой a и точка R на прямой b, которая содержит истинные расстояния.

Заключая раздел перспективы, сделаем несколько замечаний, связанных с выбором элементов перспективы. Перспектива, полученная при выборе картины в виде вертикальной плоскости с углом её наклона к координатной плоскости оригинала не равным нулю (как показано на рис. 93 и 94 угол ϕ ≠ о о ), часто именуется угловой. В ряде специальных примеров выбирается картина, параллельная фасаду здания, объединённому с плоскостью xOz, при этом угол ϕ равен 0 °. Такая перспектива называется фронтальной. Построение на таком чертеже перспективы выполняются с одной точкой схода. Чаще всего такой точкой является главная точка Р картины. В таких перспективах активно используется метод лучевого с ечения (примером является построение точек 12 и 22 в примере на рис. 93 и 94). Фронтальные перспективы часто применяются при построении перспектив интерьеров помещений, а также перспектив целых улиц или микрорайонов, когда основные протяжённости объектов идут в направлении, перпендикулярном картинной плоскости от зрителя. Основные правила и построения в таких перспективах сохраняются.

119

7. Проекции с числовыми отметками

Проекции с числовыми отметками, так же как аксонометрия и перспектива, являются чертежами на одной плоскости проекций. При этом используется ортогональное проецирование оригинала на плоскость координат x0y. Недостающая координата, а именно аппликата, заменяется числом, выражающим расстояние от точки оригинала до плоскости проекций. Совокупность ортогональной проекции с этим числом и называется проекцией с числовой отметкой, которая является обратимым чертежом оригинала.

Рис. 110

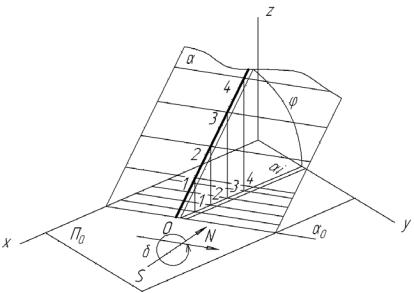
На рис. 110 показана геометрическая схема получения проекций с числовыми отметками. Из чертежа видно, что плоскость П0 , которая называется в этой схеме нулевой поверхностью, делит пространство на две части, с положительными и отрицательными числовыми отметками. Так отметка точки А положительна, отметка точки В отрицательна, а отметка точки С, принадлежащей нулевой поверхности (плоскости x0y), равна нулю.

Прямая может быть задана двумя инцидентными ей точками. На рис. 110 прямая задана отрезком DE. Рассмотрим некоторые особенности задания прямых в проекциях с числовыми отметками. Обозначим длину горизонтальной проекции отрезка DE буквой L. Будем называть L заложением прямой, отрезком которой является DE. Составим отношение разности hD - hE к заложению L. Это отношение является величиной тангенса угла

наклона ϕ прямой DE к плоскости П0 . Величина i = tg ϕ называется уклоном прямой по отношению к плоскости П0 . Заложение прямой, соответствующее единице превышения числовых отметок точек прямой, называется ин-

120

тервалом l. Из определений уклона и интервала следует, что они являются взаимообратными величинами, т. е. l = 1 / i .

В ряде задач бывает полезным определение на отрезке прямой точек, отстоящих друг от друга на расстояние интервала, а также точек, имеющих отметки в виде целых чисел. Последняя задача называется градуированием прямой.

Проградуировать проекцию прямой можно, если определить на ней точки с постоянной разностью отметок, равной единице.

На рис. 111 плоскость проекций x0y совмещена с плоскостью страницы данного учебника.

Рис. 111

Процесс градуирования прямой, заданной двумя точками, можно представить графически, рис. 111. Отрезок прямой АВ задан числовыми отметками конечных точек в масштабе М 1:1000 м. Восстановим в точке А перпендикуляр к проекции отрезка. Примем его за совмещённую с плоскостью чертежа «рейку» высотных отметок точек отрезка. Отложим на рейке в масштабе чертежа высотные отметки ряда точек отрезка прямой АВ. Тогда точка на рейке, имеющая отметку 34 будет отстоять от отметки точки А35 на расстояние по рейке одного миллиметра. На рис. 111 на рейке высотных отметок показаны отметки точек, идущих через 10 мм, а именно 10, 20, 30. Отметка точки А имеет значение 35, а отметка точки В - 10. Построив с помощью рейки совмещённые с полем чертежа положения точек А и В, и соединив их, получаем совмещённое изображение отрезка прямой. Путём пропорционального деления, показанного на чертеже рис. 111, можно построить на проекции отрезка АВ точки с отметками 20 и 30. Вообще, используя графическую связь рейки с проекцией отрезка через совмещённое изображение отрезка, можно построить на проекции точку с

121

любой заданной на рейке высотной отметкой. В качестве примера на рис. 111 показано построение на проекции отрезка АВ точки Е с отметкой 26. Что же касается интервала на отрезке АВ, то он получается отложением на рейке точек, высотные отметки которых отличаются на один миллиметр. Например, отметки точки А35 и точки с отметкой 34. Соответствующий интервал будет 2,34 мм.

На рис. 111 показано построение точки на прямой АВ, отметка которой равна 0,0. Эта точка М0 является следом прямой на нулевой поверх-

ности П0 .

Конечно, интервал заданной прямой можно получить вычислениями. Для этого надо вычислить уклон прямой, если он не задан, но заданы ч и- словые отметки двух точек прямой. Если же уклон задан, взять обратную его величину в качестве интервала.

Прямую можно задать одной точкой с числовой отметкой и величиной уклона. В этом случае дополнительно показывается в виде стрелки направление по прямой от положительных к отрицательным отметкам точек на ней. Часто такие направления называются «падением» прямой.

Рис. 112 Рис. 113

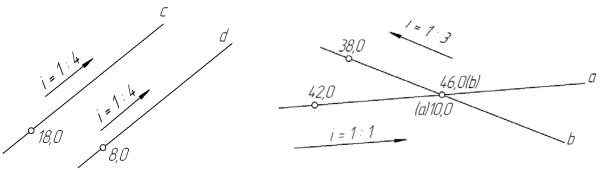
На рис. 112-113 заданы проекции двух прямых. Используя эти проекции, можно определить взаимное положение прямых в пространстве. Представляется очевидным, что параллельные в пространстве прямые должны иметь параллельные проекции на плоскости П0 , равные уклоны и одинаковые падения, показанные стрелками. Такими являются прямые с и d, показанные на рис. 112.

Если же проекции прямых пересекаются, то такие прямые могут пересекаться в пространстве либо быть скрещивающимися. У пересекающихся прямых точка пересечения должна иметь одну и ту же отметку для точек, расположенных на двух прямых. У скрещивающихся прямых эта точка имеет двойную отметку. На рис. 113 показаны проекции прямых a и b, которые пересекаются. Однако в пространстве это могут быть скрещивающиеся прямые. Для решения вопроса о положении этих прямых необходимо их проградуировать. Из чертежа рис. 113 видно, что у прямых з а-

122

даны уклоны и по одной точке на каждой прямой. Так на прямой a задана точка с отметкой 42,0, а на прямой b − точка с отметкой 38,0. Заданы ве-

стояние от заданных точек до точки пересечения прямых, с учетом интервалов, находим, что отметка точки пересечения проекций на прямой a равна 11, а отметка на прямой b − 46. Отсюда делаем вывод, что прямые a и b скрещиваются, В точке пересечения проекций прямых прямая b перекрывает прямую a, т. к. отметка точки, лежащей на прямой b больше, чем у точки, лежащей на прямой a.

Рассмотрим теперь задание плоскостей и поверхностей в проекциях с числовыми отметками. Наиболее распространённым определителем плоскости на чертеже являются три точки плоскости, не лежащие на одной прямой. Примером являются точки А, В, С, показанные на рис. 114.

Рис. 114

Построим какую-нибудь горизонталь в заданной плоскости. Для этого соединим точку В с точками А и С прямыми линиями. Теперь у нас есть возможность определить уклоны прямых АВ и ВС и, следовательно, интервалы. Как мы знаем, это можно сделать при помощи простейших вычислений, а также графически.

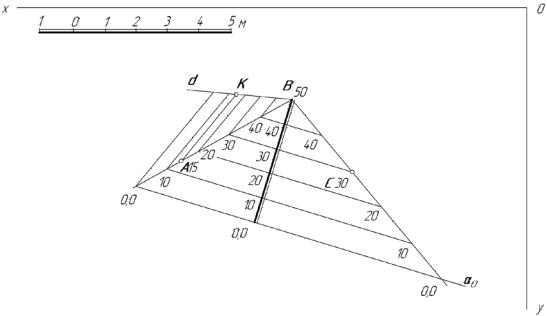
На рис. 114 показан метод пропорционального деления для построения интервала на прямой АВ. Через точку В проводим произвольную прямую d, на которой откладываем три равных отрезка произвольной длины. При проведении операции пропорционального деления концы этих отрез-

123

ков будут соответствовать точкам с отметками 40, 30 и 20 на проекции прямой АВ. Для осуществления пропорционального деления отрезка АВ необходимо отложить на прямой d от конца третьего отрезка часть такого же отрезка. На рис. 114 эта часть равна половине отрезка, т. к. отметка точки А равна 15. Отложив на вспомогательной прямой d отрезок, по длине равный половине длины отрезков, делящих d, получим точку К, которую соединим с точкой А на проекции отрезка АВ. Теперь достаточно через точки деления прямой d провести прямые, параллельные прямой АК, до пересечения с проекцией прямой АВ. Точки пересечения дадут отрезки, градуирующие прямую АВ. На рис. 114 градуирование произведено до точки 0.0, т. е. до следа прямой АВ на плоскости П0 . Построения, связанные с градуировкой прямой ВС аналогичны приведённым построениям для прямой АВ. При этом получена точка 0.0 на прямой ВС. Соединяя нулевые точки прямых АВ и ВС, получаем след плоскости АВС на П0 (след обозначен символом α0 ). Прямые,

параллельные следу α0 будут горизонталями плоскости АВС. Эти горизонтали на чертеже, показанном на рис. 114, могут быть построены без наличия следа плоскости, путём соединения точек на прямых АВ и ВС, имеющих равные отметки.

Прямая, перпендикулярная горизонталям плоскости, является линией ската плоскости. Линия ската, как и любая другая линия, может быть проградуирована. Известно, что линия ската плоскости наклонена по отношению к своей ортогональной проекции под углом ϕ, который измеря-

плоскости, которые перпендикулярны линии ската, см. рис. 115.

Рис. 115

124