4.3.3.Непрерывность монотонной функции

Для дальнейшего исследования будет полезной следующая теорема.

Теорема 4.4. Пусть возрастает (или убывает) на промежутке, причём множество её значений образует промежуток. Тогда– непрерывная на функция.

Доказательство. Для доказательства вспомним, что если строго монотонна на промежутке, то, согласно следствию теоремы 3.7.2, в любой внутренней точкеэтого промежутка существуюти. Если эти числа равны друг другу, то они, ввиду монотонности, равныи. Если же эти значения не равны друг другу, то во множестве значенийY функции имеется “пробел” между точкамии, опять же ввиду монотонности. Но, по условию, множество значенийобразует промежуток, в котором, по определению промежутка, не может быть “пробелов”.

4.3.4. Непрерывность показательной функции, логарифмической функции и степенной функции

Функция монотонна (возрастает при, убывает при ) и множеством ее значений приявляется бесконечный промежуток – множество всех положительных чисел. По доказанной теореме 4.4 функциянепрерывна на всей числовой оси.

Функция монотонна (возрастает при, убывает при ) и приее множество значений есть. По доказанной теореме, непрерывна на .

Функцияопределена на, причем . По доказанному выше, непрерывная функция на, функциянепрерывна при всех, поэтому, по теореме о непрерывности сложной функции,- непрерывная нафункция.

4.3.5.Непрерывность тригонометрических функций

Сначала докажем непрерывность функции. При вычислении предела было установлено, что если

, то . Ввиду нечетности функцийи, при

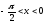выполняются неравенства. Из этого сразу следует, что при

выполняется неравенство . Пустьпроизвольная точка. Докажем, что. Это равносильно тому, что. В свою очередь, это равносильно тому, что. Так как, по доказанному выше,,. Кроме того, функция, очевидно, ограниченная. По свойствам бесконечно малых, получаем требуемое.

Функция непрерывна по теореме о непрерывности сложной функции, так как

y

, – непрерывная функция и– тоже непрерывная функция.

Функция непрерывна во всех точках, кроме. В этих, последних, она не определена и при любом доопределении в них имеет разрыв второго рода.

Функция непрерывна во всех точках, кроме точек, где она не определена и при любом доопределении в них имеет разрыв второго рода.

4.3.6.Непрерывность обратных тригонометрических функций

Непрерывность функции

Функция определена на отрезке [-1, 1], возрастает на нём и множеством её значений является отрезок [

]. По теореме 4.4, непрерывна на [-1, 1].

Непрерывность функции следует из тождества , откудафункция, также непрерывная на [-1, 1].

Докажем непрерывность функции

Функция определена и возрастает на всей числовой прямой. Множество значений – интервал (

). Поэтому непрерывна на всей числовой прямой.

Непрерывность функцииследует из равенства :.

§4.4. Символы ,. Вычисление

, ,

4.4.1. Символы ,

Пусть ,определены в.

Определение 4.6 Говорят, что есть «о-малое» от при

(Обозначение:,

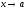), если существует ,– бесконечно малая прифункция такая, что.

Определение 4.7. Говорят, что есть «о-большое» от при

(Обозначение: ,

), если существует – ограниченная в, такая, что.

Примеры.

1. при

2. , т.к. , а;

3. , при

4. ∞, т.к. , ипри∞.

Вообще, если и, тои если

и ∞ то.

Из свойств бесконечно малых величин следуют такие свойства символов,.

Теорема 4.5.Если ,, то,; все соотношения выписаны при

.

Доказательство. Действительно, ,,гдебесконечно малые при

функции и , а.В фигурных скобках стоят бесконечно малые при

функции.

Теорема 4.6. , т.е. если , топри

.

Доказательство. Действительно, если , а, т. е.,, гдебесконечно малые при

функции, то , где

–бесконечно малая при функция, что и означает справедливость доказываемого равенства . Для большей ясности повторим, что равенство следует понимать так: если, топри

.

Теорема 4.7. , ,

.

Доказательство. Эти свойства сразу следуют из того, что произведение бесконечно малой величины на ограниченную есть бесконечно малая величина.

Символы, очень удобны при вычислении пределов.