Глава 6. Производные и дифференциалы

§ 6.1. Производная и её основные свойства

6.1.1. Дифференцируемость функции

Пусть определена в окрестности точки .

Определение 6.1.1. Числовую функцию называютдифференцируемой в точке , если для всехимеет место равенство

, (1)

где число не зависит от , априи бесконечно малая функ­циянепрерывна в точке, т.е..

Числовую функцию называютдифференцируемой на множестве, еслидифференцируема в каждой точке.

Примеры. Линейная функция дифференцируема на всей числовой прямой, действительно,. Аналогично, квадратичная функциядифференцируема. Действительно, , .

Теорема 6.1.1. Функция , дифференцируемая в точке, непрерывна в этой точке.

Доказательство. В силу формулы (1), .

Эта теорема даёт необходимое, но не достаточное условие дифференцируемости функции. Пример функции (позже мы докажем, что эта функция не дифференцируема в точке), показывает, что утверждение, обратное теореме 6.1.1, неверно.

6.1.2.Производная

Пусть определена в окрестности точки .

По­скольку на множестве определена функция и- предельная точка множества, рассмотрим вопрос о существовании предела отношения в точке .

Определение 6.1.2. Число (если оно существует) называютпроизводной функции 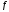в точкеи обозначают символом.

Итак,

, (2)

при условии, что предел существует.

Для обозначения производной также используется символ .

Производная представляет собой математическую модель большого количества величин, имеющих важнейшее значение в естественных и гуманитарных науках.

Например, скорость прямолинейного дви­жения есть производная перемещения как функции времени. Часто полез­но, по аналогии с этим, трактовать и производную любой функции в точке как скорость изменения функции в этой точке.

Важным понятием в экономике являются предельные величины. Например, пусть обозначает величину издержек производства, рассматриваемую как функцию от количествавыпускаемой продукции. Если прирост продукции, приращение издержек производства , тосреднее приращение издержек производства на единицу продукции. Производнаявыражаетпредельные издержки производства и является приблизительной характеристикой дополнительных затрат на производство единицы дополнительной продукции.

Вполне аналогично определяются предельная выручка, предельный доход, предельная полезность и т.п.

Предельные величины также часто называют маржинальными.

Рассмотрим простые примеры вычисления производных.

Примеры. Линейная функция имеет производную в каждой точке, и ее производная- постоянная.

Действительно,

.

В частности, постоянная имеет всюду производную, равную нулю, а то­ждественная функция - производную, равную единице.

Квадратичная функция имеет производную в каждой точке, и ее производная равна.

Действительно,

.

Рассмотрим пример непрерывной функции, не имеющей производной.

Функция модуль не имеет производной в точке 0.

Действительно, не существует, поскольку предел приэтого отношения равен 1, а предел приравен -1 и, следовательно, предел прине существует, так как эти односторонние пределы различные. В этом примере мы встретились с ситуацией, когда существуют односторонние пределы и . Эти пределы называются, соответственно, правой и левой производной и обозначаются . Для существования производной, по теореме 3.5.1, необходимо и достаточно, чтобы существовали и были равны друг другу.

Теорема 6.1.2. Функция 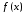, дифференцируемая в точке, имеет в этой точке производную, и эта производная равна коэффициентув представлении функциипо формуле (1).

Доказательство. Согласно определению 6.1.1, -- предельная точка области определения функции 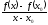. В силу формулы (1), для всех .Так как при, то на основании формулы (2) заключаем, чтосуществует и равна.

Теорема 6.1.2 показывает, что функция , дифференцируемая в точке, представима в виде

, (3)

где при.

Из этой теоремы следует, что функция не является дифференцируемой в точке 0, поскольку не имеет производной в этой точке.

Теорема 6.1.3. Функция 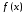, имеющая производную в точке, дифференци­руема в этой точке.

Доказательство. По условию, существует . Следовательно, по теореме о представлении функции, имеющей предел в точке,

, где при . (4)

Положим

Тогда также прии для всех спра­ведлива формула (3). Тем самым, дифференцируема в точке, причём в определении дифференцируемости).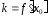

Теоремы 6.1.2 и 6.1.3 означают, что функция дифференцируема в дан­ной точке тогда и только тогда, когда она имеет в этой точке производную. Нахо­ждение производной функциидля функцииназываютдифференцировани­ем этой функции.