Глава 4. Непрерывность функции

§4.1. Непрерывность функции в точке. Свойства непрерывных функций

Пусть функция определена в некоторой окрестности точки

.

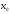Определение 4.1.1 Функция называется непрерывной в точке

, если , т.е.

Для непрерывности в точке 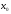используется обозначение.

Теорема 4.1.1. Если функции инепрерывны в точке

, то сумма, разность, произведение и, если , то и частное этих функций - тоже непрерывны в точке

.

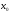Теорема непосредственно следует из теоремы о пределе суммы, разности, произведения и частного двух функций, имеющих пределы и определения непрерывности.

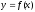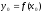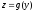Теорема 4.1.2. (непрерывность сложной функции). Пустьнепрерывна в точке, причем. Пустьнепрерывна в точке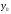. Тогда сложная функция 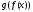непрерывна в точке .

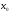Доказательство. То, что , означает: .

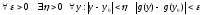То, что , означает:

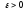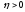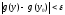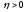Поэтому для произвольного можно сначала выбрать число так, чтобы из неравенстваследовало неравенство. Затем по этому числунайдем число такое, что как только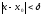, так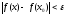. Но тогда и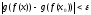, что и требовалось доказать.

Несколько сложнее теорема о пределе сложной функции.

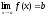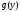Теорема 4.1.3. Пустьопределена в проколотой окрестности точкиa, . Пустьопределена в проколотой окрестности точкиb и .

Пусть, кроме того, выполняется хотя бы одно из двух условий:

1. Непрерывна в точке;

2. Существует такая , что.

Тогда существует и этот предел равен с.

Доказательство похоже на доказательство предыдущей теоремы.

То, что 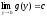означает, что.

То, что 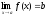означает, что.

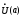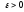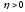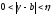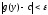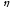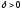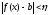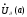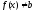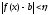Если потребовать, чтобы в некоторой проколотой окрестности точки a , то тогда можно по произвольному найти сначала число такое, что если, то. Теперь по этомунаходимтак, чтобы изследовало неравенство. Пересекаем проколотые окрестности и . Это пересечение содержит некоторую проколотую окрестность точки a, и, если x принадлежит этой окрестности, то и , т.е.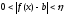, следовательно,. В этом случае теорема доказана. Если же

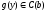, то , поэтому выбирая по соответствующее 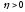, а потом по этому– соответствующее число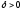получаем, что как только, так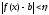 и, значит, .

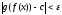Примечание 1. Обычно при вычислении пределов мы используем либо замены переменной под знаком непрерывной функции и тогда выполняется условие 1, либо монотонные замены переменной и тогда выполняется условие 2.

Примечание 2. Если не выполняется ни одно из условий этой теоремы, то может оказаться, что предел 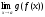не существует, либо существует, но не равен с.

Приведём пример, когда предел сложной функции не существует:

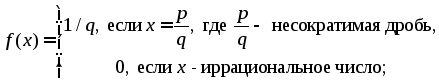
При стремлении x к 0 функция 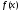имеет пределом число 0. В этом можно убедиться так: для любогопустьудовлетворяет неравенству Выберемчисло так, чтобы выполнялись неравенства . Тогда если, то не может быть рациональным числом со знаменателем, большим, чем . Поэтому

При стремлении к 0 функция

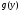имеет предел, равный 1.

Однако функция

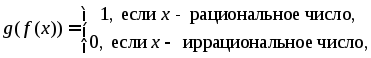
не имеет предела при . Действительно, взяв две последовательности, стремящиеся к нулю, одна из которых состоит из рациональных чисел, например,, а другая – из иррациональных чисел, например, мы получим, что Это означает, что не выполнены условия существования предела по Гейне.

Приведём пример, когда предел сложной функции существует, но не равен с.

Пусть

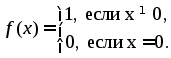
Очевидно, .

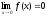Пусть .

Тогда .

Однако

Поэтому .