
- •Глава 6. Производные и дифференциалы
- •§ 6.1. Производная и её основные свойства
- •6.1.1. Дифференцируемость функции
- •6.1.2.Производная
- •6.1.3. Касательная к графику функции
- •§ 6.2. Вычисление производных
- •6.2.2. Производные элементарных функций
- •6.2.3. Производная обратной функции
- •6.2.4. Производные обратных тригонометрических функций
- •6.2.5. Производная сложной функции
- •6.2.6. Производная функции, заданной параметрически
- •§6.3. Дифференциал
- •6.3.1.Понятие дифференциала числовой функции
- •6.3.2. Геометрический и механический смысл дифференциала
- •6.3.3. Инвариантность формы первого дифференциала
- •6.3.4.Дифференциал суммы, произведения и частного функций
- •§6.4. Производные и дифференциалы высших порядков
- •6.4.1. Последовательные производные
- •6.4.3. Линейное свойство производных высших порядков
- •6.4.5. Вторая производная функции , заданной параметрически
- •6.4.6. Дифференциалы высших порядков
- •§ 6.5. Эластичность и её свойства
6.1.3. Касательная к графику функции
Как и нахождение скорости неравномерного движения, нахождение касательной к кривой линии - одна из основных задач, решение которых привело к созданию дифференциального исчисления. Рассмотрим частный случай задачи о касательной, когда линией служит график функции.
Определение
6.1.3.
Пусть числовая функция
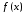 определена на невырожденном промежутке
определена на невырожденном промежутке и непрерывна в его точке
и непрерывна в его точке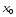 (так что расстояние
(так что расстояние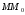 от
соответствующей точки
от
соответствующей точки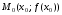 графика
до его точки
графика
до его точки
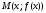 ,
,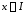 ,
стремится к нулю при
,
стремится к нулю при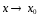 ) .Касательной
к
графику функции
) .Касательной
к
графику функции
 в точке
в точке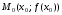 называют такую прямую, проходящую через
называют такую прямую, проходящую через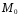 ,
что отношение расстояния
,
что отношение расстояния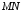 от
точки
от
точки
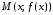 до
этой прямой к расстоянию
до
этой прямой к расстоянию от
от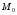 до
до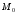 стремится к нулю при
стремится к нулю при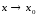 (т.е. что
(т.е. что
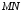 бесконечно
мало по сравнению с
бесконечно
мало по сравнению с
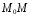 при
при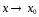 ).
).
(рис.
14). Таким образом, кривая, обладающая в
точке
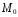 касательной, почти сливается с ней
вблизи этой точки.
касательной, почти сливается с ней
вблизи этой точки.
Теорема
6.1.4. Если
функция
 ,
определенная на промежутке, дифференцируема
в его точке
,
определенная на промежутке, дифференцируема
в его точке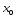 ,
то график этой функции имеет в
соответствующей точке
,
то график этой функции имеет в
соответствующей точке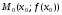 касательную, причем угловой коэффициент
касательной равен
касательную, причем угловой коэффициент
касательной равен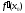 .
.
Доказательство. По условию и по теореме 6.1.2, равенство

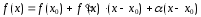 ,
(5)
,
(5)
выполняется
для всех
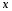 ,
принадлежащих некоторой окрестности
,
принадлежащих некоторой окрестности![]() точки
точки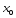 ,
и
,
и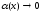 при
при .
Прямая
с угловым коэффициентом
.
Прямая
с угловым коэффициентом
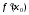 ,
проходящая через точку
,
проходящая через точку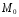 ,
имеет уравнение
,
имеет уравнение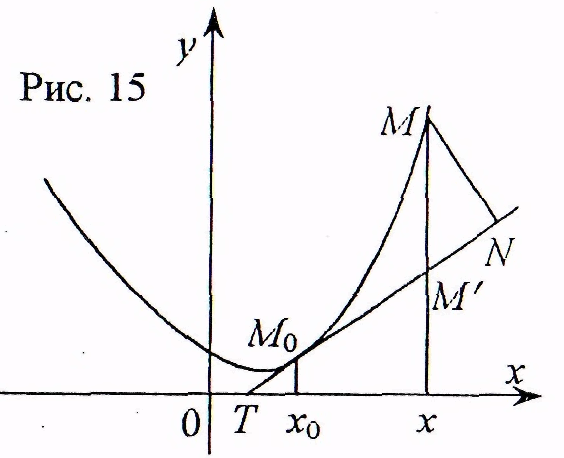
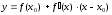 .
(6)
.
(6)
Пусть
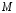 - точка графика с абсциссой
- точка графика с абсциссой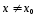 и
и![]() (рис. 15),
(рис. 15),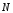 -
проекция этой точки на прямую (6) и
-
проекция этой точки на прямую (6) и
 - точка
этой прямой с абсциссой
- точка
этой прямой с абсциссой
 .
Тогда
направленный отрезок
.
Тогда
направленный отрезок
 равен
равен
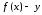 ,
так
что, вычитая (8) из (7), получаем
,
так
что, вычитая (8) из (7), получаем
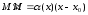 .
Так
как
.
Так
как
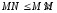 ,
а
,
а
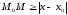 ,
то
,
то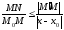 .
Но
.
Но
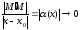 при
при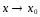 .
Следовательно,
.
Следовательно,
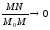 при
при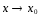 ,
т.е.
(7) - уравнение касательной к графику
функции
,
т.е.
(7) - уравнение касательной к графику
функции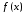 в
его точке
в
его точке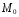 .
.
Таким образом, нахождение углового коэффициента касательной (как и нахождение скорости) приводит к вычислению производной.
Замечание
1.
Секущая
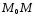 имеет
угловой коэффициент
имеет
угловой коэффициент (см. рис. ). Таким образом, теорема 6.1.4
показывает, что справедливо следствие.
(см. рис. ). Таким образом, теорема 6.1.4
показывает, что справедливо следствие.
Следствие.
Угловой
коэффициент касательной в точке
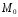 есть предел углового коэффициента
секущей
есть предел углового коэффициента
секущей при
при
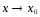 .
.
§ 6.2. Вычисление производных
6.2.1.Дифференцирование суммы, произведения и частного
Теорема 6.2.1
Пусть
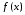 имеет
производную в точке
имеет
производную в точке
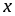 .
Тогда для любой постоянной
.
Тогда для любой постоянной
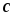 справедлива
формула:
справедлива
формула:
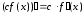
(постоянный множитель можно вынести за знак производной).
Пусть
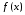 и
и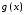 имеют производные в точке
имеют производные в точке
 .Тогда
существует производная суммы этих
функций, причём
.Тогда
существует производная суммы этих
функций, причём
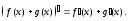 .
.
Пусть
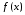 и
и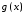 имеют производные в точке
имеют производные в точке
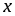 .Тогда
существует производная произведения
этих функций, причём
.Тогда
существует производная произведения
этих функций, причём
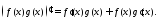 .
.
Пусть
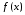 и
и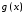 имеют производные в точке
имеют производные в точке
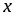 и пусть
и пусть
 .
Тогда
существует производная частного этих
функций, причём
.
Тогда
существует производная частного этих
функций, причём
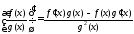 .
.
Доказательство.
Приращение функции
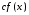 в точке
в точке
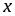 равно
равно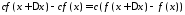 .
По условию, существует
.
По условию, существует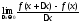 , следовательно, существует и
, следовательно, существует и
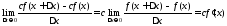 ,
что и требовалось доказать.
,
что и требовалось доказать.
Приращение функции
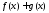 в точке
в точке
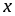 равно
равно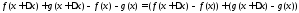 ,
,
поэтому справедливы равенства

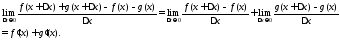
Аналогично, для произведения
 имеем
имеем
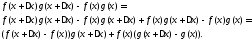
При
![]() выполняются
соотношения
выполняются
соотношения
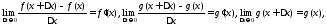
следовательно, по теореме 3.3.1 получаем
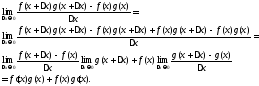
Сначала докажем лемму
Лемма.
Пусть
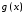 имеют производную в точке
имеют производную в точке
![]() и пусть
и пусть
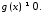 Тогда
Тогда
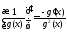 .
.
Доказательство леммы. Рассматриваемое приращение имеет вид:
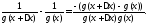
По
лемме 3.3.2
предел функции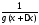 равен
равен
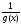 .
Следовательно,
.
Следовательно,
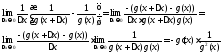 .
.
Лемма доказана.
Утверждение 4 теоремы 6.2.1 сразу следует из её утверждения 3 и доказанной леммы.
