
Вышка задачи
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Методические указания к практическим занятиям и самостоятельной работе студентов
Самара 2005
3
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Кафедра высшей математики
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Методические указания к практическим занятиям и самостоятельной работе студентов
Утверждены редакционноиздательским советом университета 19 января 2005 г.
Самара 2005
4
Составители: Антонова Н.Н., Голодова Е.С., Хлебникова М.Ю.
УДК 517.3(07)
Определенный интеграл: Методические указания / Сост.: Антонова Н.Н., Голодова Е.С., Хлебникова М.Ю.; Самарск. гос. арх. -строит. ун-т, Самара,
2005.
Данные методические указания являются разработкой практических занятий по теме «Определенный интеграл». Подробно изложены методы вычисления определенного и несобственного интеграла, а также геометрические, физические и экономические приложения. Методические указания содержат варианты индивидуальных заданий, позволяющих организовать самостоятельную работу студентов при изучении темы. Методические указания предназначены для студентов I курса специальностей 290300(«Промышленное и гражданское строительство»), 290500 («Городское строительство и хозяйство»), 291000(«Автомобильные дороги и аэродромы»), 290400(«Гидротехническое строительство»), 290700 («Теплогазоснабжение и вентиляция»), 290800 («Водоснабжение и водоотведение»), 330200 («Инженерная защита окружающей среды»), 290600 («Производство строительных материалов, изделий и конструкций»), 291300 («Механизация и автоматизация строительства») и составлены в соответствии с рабочим планом кафедры высшей математики.
Настоящие методические указания не могут быть полностью или частично воспроизведены, тиражированы ( в том числе ксерокопированы) без разрешения Самарского государственного архитектурно-строительного университета.
© Самарский государственный архи- тектурно-строительный университет,
2005
5

Составители: Н.Н.Антонова ,Е.С. Голодова , М.Ю. Хлебникова.
Определенный интеграл
Методические указания
Редактор Л. И. Глезерова Технический редактор А.И. Непогодина Корректор Е.М. Фоменкова
Подписано в печать 29.08.05.Формат 60×84 116
Бумага офсетная. Печать оперативная. Уч.-изд. л. 3,0. Усл. печ. л. 3,1.Тираж 610 экз.
Самарский архитектурно-строительный университет 443001 Самара, ул. Молодогвардейская, 194.
6
|
|
|
I. Определенный интеграл и его свойства |
|
|
||||||||
1.Задачи, приводящие к понятию определенного интеграла |
|
|
|||||||||||
|
Пусть f(x), x |
a;b — неотрицательная непрерывная функция. Плоская фигу- |
|||||||||||
ра aABb (рис. 1), ограниченная отрезком оси абсцисс, отрезками вертикальных пря- |
|||||||||||||
мых х=а и х=b и графиком заданной функции f(x), называется криволинейной тра- |
|||||||||||||
пецией. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем площадь этой криволинейной трапеции. Для этого отрезок [а;b] точ- |
||||||||||||
ками |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
a |
b |
a i,i |
0,1,...,n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
разобьем на n равных по длине отрезков [a;x1], [х1;х2], ..., [хn-1;b]. Обозначим через mi |
|||||||||||||
и Мi, соответственно, наименьшее и наибольшее значения функции f(x) на отрезке |
|||||||||||||
[xi-1;xi], где i=1, ..., n. Тогда криволинейная трапе- |
|
|
|
|
|||||||||
ция аАВb разобьется на n частей. Очевидно, пло- |
y |
|
В |
|
|||||||||
щадь 1-й части не меньше mi (xi-xi-1) и не больше |
|
y=f(x) |
|
||||||||||
|
|
|
|||||||||||
Mi (xi-xi-1). Поэтому площадь всей криволинейной |
|
|
|
|
|||||||||
трапеции аАВb не меньше суммы |
|
|
|
|
А |
|
|
||||||
|
|
|
|
|
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
m1 x1 ... |
mn |
xn |
mi |
xi |
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
и не больше суммы |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
n |
|
xi , |
|
0 |
x0=a x1 xi-1 xi |
xn-1 xn=b |
x |
|
|
|
M1 x1 ... |
M n |
xn |
Mi |
|
|
Рис. 1 |
|
|
||
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
xi |
хi |
xi 1 . Обозначив эти суммы, соответст- |
|
|
|
|
||||||
венно, через sn и Sn, получим, что площадь SaABb |
криволинейной трапеции аАВb |
||||||||||||
удовлетворяет неравенствам |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
sn |
SaABb |
Sn . |
|
|
|
|
|
Здесь sn—площадь ступенчатой фигуры, которая содержится в данной криво- |
||||||||||||
линейной трапеции, a Sn—площадь ступенчатой фигуры, которая содержит данную |
|||||||||||||
криволинейную трапецию (pиc. l). Интуитивно ясно, что при достаточно мелком |
|||||||||||||
разбиении отрезка [а; b], т. е. при достаточно большом n, площади sn и Sn указанных |
|||||||||||||
выше фигур мало отличаются друг от друга и от площади криволинейной трапеции. |
|||||||||||||
Определение. Пусть f(х), х [а; b],— непрерывная неотрицательная функция. Тогда, если пределы последовательностей sn и Sn существуют и равны, то их
значение называется площадью криволинейной трапеции.
На каждом отрезке xi 1; xi  выберем произвольную точку сi, xi 1 ci xi . Для нее
выберем произвольную точку сi, xi 1 ci xi . Для нее
справедливы неравенства |
|
mi f ci M i , |
(1.1) |
где i=1, ..., n. Умножим каждое из неравенств (1.1) на xi |
xi xi 1 и полученные не- |
7

равенства сложим. Тогда придем к неравенствам
n |
|
|
|
|
|
sn |
f |
ci |
xi Sn |
|
(1.2) |
i |
1 |
|
|
|
|
где сумма |
|
|
|
|
|
|
|
|
|
n |
|
f ci xi ... |
f |
cn |
xn |
f ci xi |
(1.3) |
|
|
|
i |
1 |
|
называется интегральной суммой функции f(х) на отрезке [а; b]. Переходя в неравенствах (1.2) к пределу при n 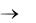 , заключаем, что предел интегральной суммы (1.3) существует, не зависит от выбора точек сi и от способа разбиения [а; b] на частичные отрезки и равен площади фигуры аАВb:
, заключаем, что предел интегральной суммы (1.3) существует, не зависит от выбора точек сi и от способа разбиения [а; b] на частичные отрезки и равен площади фигуры аАВb:
|
n |
|
lim |
f ci xi SaABb . |
(1.4) |
n |
i 1 |
|
|
|
С необходимостью вычисления предела интегральных сумм мы встречаемся в задачах разной физической природы, например, при введении понятия работы силы. Пусть материальная точка под действием постоянной силы F движется по прямой. Тогда положение материальной точки характеризуется координатой х. Работа А силы F вычисляется по формуле
A F x , |
(1.5) |
где x — перемещение материальной точки.
Пусть теперь материальная точка движется вдоль оси Ох под действием переменной силы f(x), причем в начале движения она находится в точке х=а, а в конце
движения — в точке х=b. Разобьем отрезок [а; b] точками xi |
a |
b a |
i |
на n частей |
||
|
||||||
|
|
|
|
n |
|
|
[хi-1, хi] одинаковой длины xi |
b a |
. На каждом отрезке [хi-1, хi] работу силы мож- |
||||
|
||||||
|
n |
|
|
|
|
|
но приближенно вычислить по формуле (1.5), т. е. считать ее равной f(сi) |
xi где сi — |
|||||
некоторая точка отрезка [хi-1, хi]. Тогда работа силы на отрезке [а; b] приближенно выражается формулой
|
n |
A |
f ci xi . |
|
i 1 |
Точность приближения будет тем лучше, чем короче отрезки [хi-1, хi], на которые разбит отрезок [а; b]. Поэтому, переходя к пределу при n 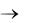 , получим равенство:
, получим равенство:
|
|
n |
A lim |
|
f ci xi , |
n |
i |
1 |
|
совпадающее по виду с равенством (1.4).
2.Понятие определенного интеграла
Из рассмотренных в п. 1 примеров видно, что к задаче о нахождении предела интегральной суммы сводятся задачи разнообразной природы.
n
Определение. Пусть дана функция f(x), х [а; b]. Если предел lim f ci xi |
|
n |
i 1 |
|
|
существует и не зависит от выбора точек сi и от способа разбиения [а; b] на час-
8
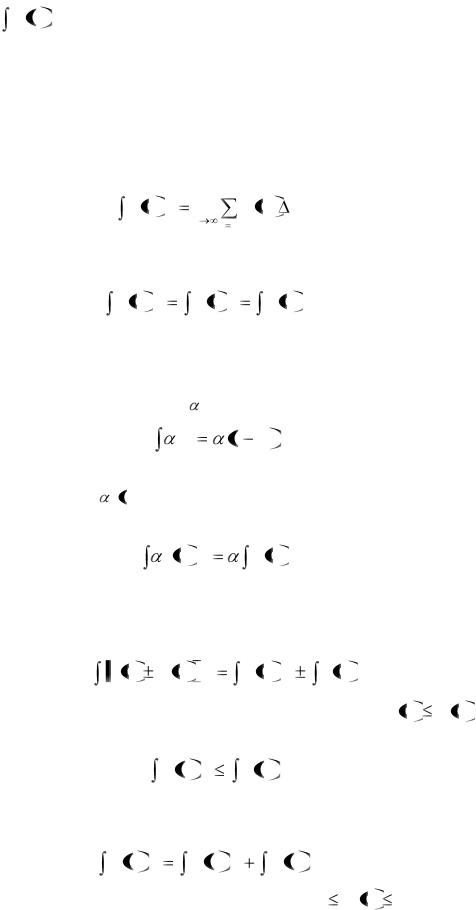
тичные отрезки, то функция f(x) называется интегрируемой на отрезке [a; b], а предел - определенным интегралом от функции f(x) на отрезке [a; b] и обознача-
b
ется символом f x dx.
a
Это обозначение читается так: «интеграл от а до b от функции f(x) по dx» или, короче, «интеграл от а до b от f(x)dx». Знак 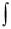 называется знаком интеграла, функ-
называется знаком интеграла, функ-
ция f(x) — подынтегральной функцией, переменная х — переменной интегрирования, выражение f(x)dx — подынтегральным выражением. Числа а и b называются пределами интегрирования, соответственно, нижним и верхним.
Таким образом, согласно определению,
b |
|
|
n |
|
|
|
f x dx |
lim f |
ci |
xi . |
|
a |
|
n |
i 1 |
|
|
|
|
|
|
||
Определенный интеграл не зависит от того, какой буквой обозначена пере- |
|||||
менная интегрирования, так что, например, |
|
|
|||
b |
b |
|
|
b |
|
f |
x dx |
f t dt |
f |
u du . |
|
a |
a |
|
|
a |
|
3. Основные свойства определенного интеграла |
|
||||
1°. Для любого действительного числа |
|
справедливо равенство |
|||
|
b |
|
|
|
|
|
dx |
|
b |
a . |
(1.6) |
a
2°. Пусть функция f(x) интегрируема на отрезке [а; b]. Тогда для любого действительного числа а, функция f x также интегрируема на [а; b] и выполняется равенство:
также интегрируема на [а; b] и выполняется равенство:
b |
b |
|
f x dx |
f x dx , |
(1.7) |
a |
a |
|
т. е. постоянный множитель можно выносить за знак интеграла.
3°. Пусть функции f(x) и g(x) интегрируемы на отрезке [а; b]; тогда их алгебраическая сумма также интегрируема на [а; b], и выполняется равенство:
b |
|
|
b |
|
b |
|
f |
x g x dx |
f |
x dx |
g x dx . |
(1.8) |
|
a |
|
|
a |
|
a |
|
4°. Если на отрезке [а; b] функции f(x) и g(x) интегрируемы и |
f x g x , то спра- |
|||||
ведливо неравенство: |
|
|
|
|
|
|
|
b |
|
b |
|
|
|
|
f |
x dx |
g x dx . |
|
(1.9) |
|
|
a |
|
a |
|
|
|
5°. При любом расположение a, b, c выполняется равенство: |
|
|||||
b |
|
с |
|
b |
|
|
f |
x dx |
f x dx |
f x dx . |
(1.10) |
||
a |
|
a |
|
c |
|
|
6°. Если на отрезке [а; b] выполняется неравенство |
m f x |
M , где m и M – не- |
||||
9
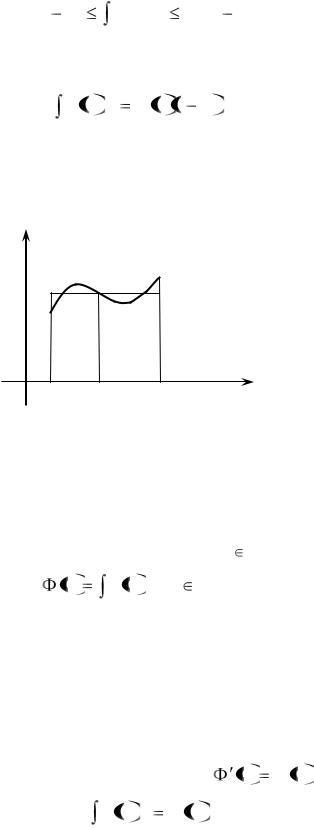
которые числа, то
|
b |
|
m(b a) |
f (x)dx M (b a) . |
(1.11) |
a
7°. Пусть функция f(x) непрерывна на отрезке [а; b]. Тогда на этом отрезке существует такая точка с, что
b
f x dx f c b a . |
(1.12) |
a
Для неотрицательной функции это свойство имеет простое геометрическое истолко-
вание: площадь криволинейной трапеции, соответствующей функции f, равна площади прямоугольника, у которого основание равно основанию трапеции, а высота равна одному из значений функции (рис. 2).
y
0 |
a |
с |
b |
x |
|
|
|
|
Рис. 2
4.Определенный интеграл с переменным верхним пределом
Пусть функция f(x) непрерывна на отрезке [а; b]. Тогда, как было отмечено выше, она интегрируема на любом отрезке [а; х], где х [а; b]. Рассмотрим функцию
|
x |
|
x |
f z dz , x [а; b]. |
(1.13) |
a
Эта функция называется интегралом с переменным верхним пределом. В формуле
(1.13) переменная интегрирования обозначена через z, так как через х здесь обозна-
чен верхний предел интеграла (он является независимой переменной, т. е. аргумен-
том функции Ф). Для этой функции справедлива следующая теорема.
ТЕОРЕМА 1. Если функция f(x) непрерывна на отрезке [а; b], то функция
Ф(х) имеет производную на отрезке [а; b], причем |
x f x , т. е. |
||
|
d x |
|
|
|
|
f z dz f x . |
(1.14) |
|
|
||
|
dx a |
|
|
Это утверждение называют теоремой о дифференцировании интеграла по верхнему пределу. Из нее следует, что любая непрерывная функция имеет первообразную, которой является определенный интеграл с переменным верхним пределом от данной функции.
10

5. Формула Ньютона — Лейбница
ТЕОРЕМА 2. Если функция f(x) непрерывна на отрезке [а; b], а функция F(x) является первообразной для f(x) на [а; b], то справедлива формула:
b |
|
f x dx F b F a . |
(1.15) |
a
Эта формула называется формулой Ньютона-Лейбница.
Часто для краткости вместо разности F(b) — F(a) пишут: F x ba , и тогда формула (1.15) принимает вид:
b |
|
b . |
|
f x dx F x |
|
(1.16) |
|
a |
|
a |
|
|
|
||
|
|
|
Формула Ньютона — Лейбница позволяет вычислять определенные интегралы в тех случаях, когда известна хотя бы одна первообразная подынтегральной функции.
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Вычислить интеграл |
x3 dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
|||
|
Для функции |
x |
|
первообразной |
|
является |
функция |
|
|
. По |
формуле Нью- |
|||||||||||||||||||||||||||||||||
|
|
|
4 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
4 |
|
1 |
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тона — Лейбница находим |
x3 dx |
|
x |
|
|
|
|
1 |
|
0 |
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4 |
|
|
|
4 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Вычислить |
|
x2 |
sin x |
7 x10 |
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя |
свойство |
3º |
и |
|
формулу |
Ньютона—Лейбница |
будем иметь, |
||||||||||||||||||||||||||||||||||
1 |
x2 |
|
sin x 7 x10 |
|
|
1 x2 dx |
1 sin xdx |
|
1 x10 dx |
|
x3 |
|
1 |
|
cos x ) |
|
1 |
7 |
x11 |
|
|
1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
dx |
7 |
|
|
|
( |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
1 |
|
|
1 |
11 |
|
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
1 |
cos1 cos1 |
7 |
|
7 |
|
|
20 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3 |
|
3 |
|
|
|
11 |
11 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
Пример. Вычислить интеграл |
f x dx , где f ( x ) |
||||
|
|
0 |
|
|
|
Используя свойство 5º, получим: |
|
||||
2 |
1 |
2 |
1 |
2 |
|
|
|
||||
|
f x dx ex dx |
3x2 dx ex |
x3 |
e 1 8 |
|
0 |
0 |
1 |
|
1 |
|
0 |
|
||||
|
|
||||
УПРАЖНЕНИЕ 1
ex ,x |
[ 0,1 ) |
. |
|
3x2 ,x |
[ 1,2 ] |
||
|
|||
1 e |
6 . |
|
1. Используя формулу Ньютона — Лейбница, вычислите интегралы:
|
2 |
2 |
б) |
5 |
x |
2 |
1 |
dx; |
в) |
|
3 |
|
dx |
; |
а) |
x 1 dx; |
|
|
|||||||||||
|
|
|
x3 |
|
|
|
|
|||||||
1 |
2 |
|
0 1 |
x 2 |
||||||||||
11
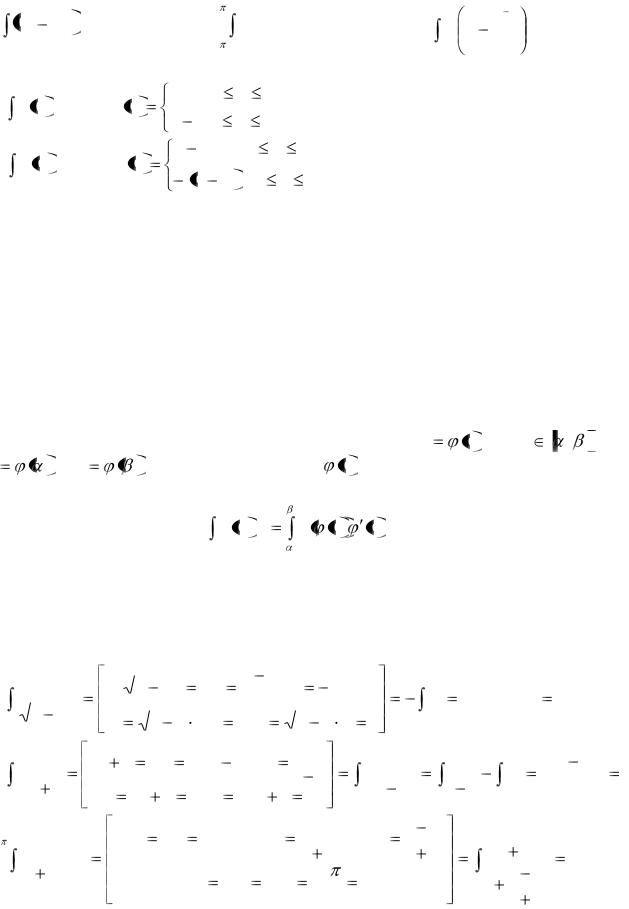
a |
|
|
|
|
|
|
/ 3 |
|
dx |
|
|
2 |
|
|
e |
x |
|
||
г) |
x |
2 |
ax dx; |
|
|
д) |
|
|
|
; |
x |
|
|
||||||
|
|
|
|
|
|
|
|
е) e |
1 |
|
dx. |
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
1 |
|
|
|
|
|
|
/ 6 cos |
x |
|
x |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2. Вычислите интегралы: |
0 |
x |
|
1, |
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
x, |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
g x dx , где |
g x |
2 |
x,1 |
x |
|
2; |
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
2, |
|
|
|
|
|
||||||
3 |
|
|
|
|
3 |
x, |
0 |
|
|
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
f |
|
x dx , где |
f x |
|
x |
4 2 , 2 |
|
|
x |
3. |
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
II. Методы вычисления определенных интегралов
1.Метод замены переменной интегрирования (метод подстановки)
При вычислении определенных интегралов, как и при вычислении неопреде-
ленных, часто используется метод подстановки (метод замены переменной ин-
тегрирования). |
|
|
|
|
|
|
|
|
Пусть функция f(x) непрерывна в любой точке x |
t , где t |
; , и пусть |
||||
a |
и b |
. Тогда, если функция |
t |
имеет непрерывную производную, то |
|||
справедлива следующая формула: |
|
|
|
|
|
||
|
|
b |
|
|
|
|
|
|
|
f x dx |
f |
t |
t dt , |
|
(2) |
a
которая называется формулой замены переменной интегрирования в определен-
ном интеграле.
Примеры
|
2 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
t |
|
|
|
|
1 |
|
|
|
|
|
|
1 dt |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
5 |
|
2x |
t ,x |
,dx |
dt |
|
|
|
|
|
ln | t |) |12 |
ln 2 . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
1. |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
( |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2t |
2 |
2 |
|
|
|
|||||||||||||||||||||||||||
|
|
5 |
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
0 ,5 |
|
|
tн |
|
|
|
|
|
5 2 0,5 |
|
2,tв |
|
|
|
|
5 |
2 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
ln 2 |
|
dx |
|
ex |
1 |
|
|
|
t ,x |
ln(t |
1 ),dx |
|
|
|
dt |
|
|
|
|
3 |
|
dt |
|
3 |
|
dt |
|
|
|
3 dt |
|
|
|
|
t 1 |
|
3 |
|
4 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
2. |
|
|
|
|
|
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
|
ln |
ln |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
0 ex |
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
ln 2 |
|
|
|
|
|
|
2 t( t 1 ) |
|
2 t 1 |
2 t |
|
t |
|
2 |
3 |
|||||||||||||||||||||||||||||||
|
|
t |
н |
e |
|
|
1 |
|
2,tв |
e |
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
tg |
x |
|
t ,x |
2arctgt,dx |
|
|
2dt |
|
|
,cos x |
1 |
|
t 2 |
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
/ 2 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
t 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3. |
|
|
|
2 |
|
|
1 |
|
t 2 |
|
1 |
|
t 2 |
|
|
|
|
1. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
0 |
|
1 |
cos x |
|
|
|
|
|
|
|
|
|
tн |
tg0 |
0,tв |
|
|
tg |
|
|
|
|
|
|
1 |
|
|
|
|
|
0 1 |
1 |
t 2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
t 2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
12
