1Опред.инт.как предел инт суммы. Пусть   определена на  . Разобьём  на части с несколькими произвольными точками   Тогда говорят, что произведено разбиение   отрезка   Далее выберем произв. точку  ,  ,

Определённым интегралом от функции   на отрезке  называется предел интегральных сумм при стремлении ранга разбиения к нулю  , если он существует независимо от разбиения   и выбора точек  , т.е.

Если существует указанный предел, то функция   называется интегрируемой на   по Риману.

2.смыслы опред.инт.Физический смысл:  1) если задана скорость как функция от времени, то путь за время Т равен интегралу от скорости по времени;  2) если задано ускорение как функция от времени, то изменение скорости равно интегралу от ускорения по времени; Геометрический смысл: если функция y(x) больше нуля на промежутке [a;b], то площадь криволинейной трапеции, ограниченной графиком функции, осью ОХ и двумя прямыми х=а и х=b, равна интегралу от этой функции по переменной х на данном промежутке.

3осн св-ва опред.инт.

1. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.  , где х, t – любые буквы. II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю. III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный. IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам. V. Постоянный множитель можно выносить за знак определенного интеграла. VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

4.Формула Ньютона-Лейбница

Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на[a, b], то

5. Метод замены переменной в определенном интеграле

При замене переменной в определенном интеграле не нужно возвращаться к исходной переменной интегрирования.

6.интегрирование по частям

Пусть u(x) и v(x) являются дифференцируемыми функциями. Дифференциал произведения функций u и vопределяется формулой

Проинтегрировав обе части этого выражения, получим

или, переставляя члены,

7. Несобственные интегралы первого рода.Определение Предположим, что функция   задана на бесконечном промежутке вида  и интегрируема на любом конечном отрезке   , где   . Таким образом, можно рассмотреть функцию, зависящую от верхнего предела, как от переменной:

Если эта функция имеет предел при   , то число   называется значением несобственного интеграла первого рода:

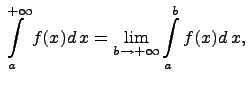
а сам определенный интеграл называется сходящимся. Если же предела не существует, то интеграл называется расходящимся и не имеет никакого числового значения.

8. Несобственные интегралы второго рода

Пусть на полуинтервале   задана функция   , интегрируемая на любом отрезке, принадлежащем данному интервалу, однако не интегрируемая на отрезке   . В точке   эта функция может быть вовсе не определена и стремиться к 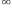  , либо вовсе не иметь никакого предела. Рассмотрим функцию

она определена при   . Эта функция может иметь предел при  (левосторонний предел). Этот предел будем называть значением интеграла от   по всему полуинтервалу   и обозначать в точности:

Определение. Пусть функция   удовлетворяет указанным выше условиям на   . Несобственным интегралом второго рода назовём определенный интеграл

значение которого равняется левостороннему пределу

Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения.

9. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР  

Пусть функция f (х)  непрерывна на отрезке [a ; b].  Если при этом f (х) ≥ 0 на [a ; b], то  площадь S криволинейной трапеции, ограниченной линиями  ,  выразится с помощью интеграла:     (1) 

Если же f (х) ≤ 0 на [a ; b], то −f (х) ≥ 0 на [a ; b].  Поэтому площадь S соответствующей  криволинейной трапеции находится по формуле    или     (2)  

Наконец, если линия у = f (х) пересекает ось Ох, то отрезок [a ; b] надо разбить на части, в  пределах которых f (х) не меняет знака, и к каждой части применить ту из формул (1) или (2),  которая ей соответствует.  

10.

Вычисление длины дуги плоской кривой

Пусть известна функция   и требуется найти длину дуги, заданной функцией   , где   .

Для определения длины дуги   необходимо вычислить определенный интеграл:

Рассмотрим случай параметрического задания кривой:

где   . В этом случае для определения длина дуги   вычисляется определенный интеграл:

Рассмотрим случай, когда кривая задается в полярных координатах   где  . Тогда для определения длины дуги   вычисляется следующий определенный интеграл:

11.

МатематическиОбъём

В общем случае математически объём тела вычисляется по следующей интегральной формуле:

,где   — характеристическая функция геометрического образа тела.

Для ряда тел с простой формой более удобным является использование специальных формул. Например, объём куба с длиной стороны, равной a, равен  .

Через плотность

Объём находится по формуле: 

12.

Вычисление площади поверхности вращения

Найдем площадь поверхности, которая образуется вращением кривой   вокруг оси   , где   .

Указанную площадь можно получить вычислением определенного интеграла:

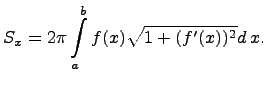Теперь рассмотрим случай, когда вращаем кривую   вокруг оси   , где 

В этом случае площадь определяется вычислением следующего определенного интеграла:

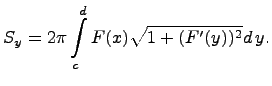
13.

Определителем квадратной матрицы второго порядка:

называется число, равное а11а22—а21а12 и обозначаемое символом

Числа а11, а12, а21, а22 называются элементами определителя матрицы второго порядка. Каждый элемент определителя обозначен буквой а с двумя индексами; первый (1) обозначает номер строки, второй (2) - номер столбца, на пересечении которых находится соответствующий элемент (например, элемент а21 принадлежит второй строке и первому столбцу определителя).

Определитель матрицы называют также детерминантом. Для определителя матрицы в контрольных по математике употребляются следующие обозначения:

Определителем квадратной матрицы третьего порядка

называют число

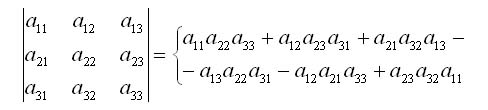
14. Метод Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы

Описание методаДля системы   линейных уравнений с   неизвестными (над произвольным полем)

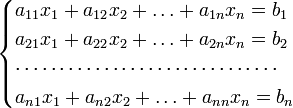
с определителем матрицы системы  , отличным от нуля, решение записывается в виде

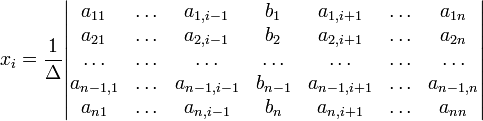
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

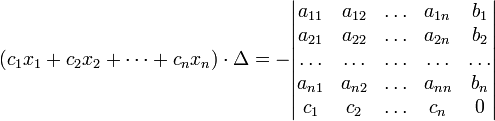
В этой форме формула Крамера справедлива без предположения, что   отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы   и  , либо набор   состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

15. Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы^[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.Матрицы допускают следующие алгебраические операции:сложение матриц, имеющих один и тот же размер;умножение матриц подходящего размера (матрицу, имеющую   столбцов, можно умножить справа на матрицу,имеющую   строк);умножение матрицы на элемент основного кольца или поля (т. е. скаляр). В математике рассматривается множество различных типов и видов  матриц.Таковы,например, единичная, симметричная,кососимметричная, верхнетреугольная

Обычно матрицу обозначают заглавной буквой латинского алфавита: пусть

,

тогда   — матрица, которая интерпретируется как прямоугольный массив элементов поля   вида  , где первый индекс означает индекс строки:  ;,второй индекс означает индекс столбца:  ;

Решение системы линейных уравнений методом Гаусса. Метод Гаусса еще называют методом последовательных исключений, поэтому основная задача, на каждом шаге исключать переменную, пока не останется одна. Если использовать матрицы, то это означает, что используя элементарные преобразования и перемещения столбцов необходимо привести расширенную матрицу к виду:

1	a'12	...	a'1r	a'1r+1	...	a'1n	b'1
0	1	...	a'2r	a'2r+1	...	a'2n	b'2
...	...	...	...	...	...	...	...
0	0	...	1	a'rr+1	...	a'rn	b'r
0	0	...	0	0	...	0	b'r+1
...	...	...	...	...	...	...	...
0	0	...	0	0	...	0	b'm

На этом шаге можно закончить преобразования, и последовательно находить корни системы уравнений в обратном порядке, но что бы этого не делать, продолжим и приведем матрицу к более удобному для нас виду:

1	0	...	0	0	...	0	b''1
0	1	...	0	0	...	0	b''2
...	...	...	...	...	...	...	...
0	0	...	1	0	...	0	b''r
0	0	...	0	0	...	0	b''r+1
...	...	...	...	...	...	...	...
0	0	...	0	0	...	0	b''m

Глядя, на эту матрицу видно, что в каждой строке присутствует лишь одна переменная и свободный член, что нам и нужно