Вышка задачи

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Пример. Вычислить площадь фигуры,

ограниченной лемнискатой r

.pdf

Скачиваний:

Добавлен:

29.03.2015

Размер:

2.37 Mб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

2. Метод интегрирования по частям

Ранее была выведена формула интегрирования по частям для неопределенного интеграла:

udv uv vdu .

Аналогичная формула справедлива и для определенного интеграла.

Пусть функции u(х) и v(x) имеют непрерывные производные на отрезке [а; b]. Тогда справедлива формула

	b	b
u x v x dx u x v x		v x u x dx .	(2.2)
u x v x dx u x v x		v x u x dx .	(2.2)
	a	a
	a

Формула (2.2) называется формулой интегрирования по частям. Она позво-

ляет сводить вычисление одного интеграла к вычислению другого. Естественно, при этом стремятся к тому, чтобы полученный интеграл был проще исходного или более удобным для изучения.

Формулу (2.2) можно записать иначе:

udv

vdu .

(2.3)

Примеры

ln x, du

ln xdx

x ln x |1e

x |1e e

dx, v

x2 cos xdx

x2 ,du

2xdx

x2 sin x |

2x sin xdx

x sin xdx

2. 0

cos xdx,v

sin x

x,du

2x cos x |0

cos xdx

sin x |0

sin x,v

cos x

УПРАЖНЕНИЕ 2

Вычислите интегралы:

x 2 dx;

x 2

;

/ 2

ln 1

x dx;

;

sin 3 x dx;

cos x

x2 dx;

/ 3

xdx .

xe2 x dx;

/ 4 sin2 x

III. Несобственные интегралы

Определенный интеграл f x dx , где промежуток интегрирования a; b ко-

нечный, а подынтегральная функция f x непрерывна на отрезке a; b , называют

ещѐ собственным интегралом.

Рассмотрим так называемые несобственные интегралы, то есть определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв.

1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)

Пусть функция f xнепрерывна на промежутке a;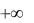. Если существует ко-

	b
нечный предел lim	f	x dx , то его называют несобственным интегралом первого
b	a
	a
рода и обозначают	f	x dx. Таким образом, по определению,
	a
				b
		f x dx	lim f x dx .		(3.1)
		a	b	a
		a		a
В этом случае говорят, что несобственный интеграл f					x dx сходится.

Если же указанный предел не существует или он бесконечен, то говорят, что инте-

грал f x dx расходится.

Аналогично определяется несобственный интеграл на промежутке ; b :

b		b
f x dx	lim	f x dx .	(3.2)

a a

Несобственный интеграл с двумя бесконечными пределами определяется формулой

	c
f x dx	f x dx	f x dx ,
		c
где с — произвольное число.

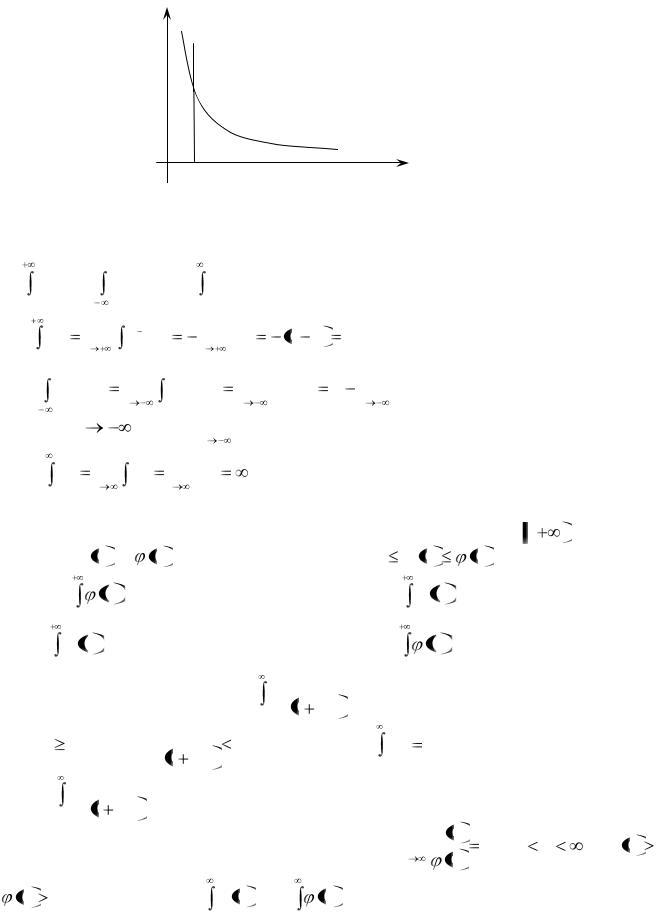
В этом случае интеграл слева сходится лишь тогда, когда сходятся оба интеграла справа. Отметим, что если непрерывная функция f x 0 на промежутке a; и

интеграл f x dx сходится, то он выражает площадь бесконечно длинной криволи-

нейной трапеции (рис. 3).

y=f(x)

0 a	x

Рис. 3 Примеры. Вычислить несобственные интегралы или установить их расходимость:

; 2)

cos xdx; 3)

x 2

1 x

lim

x 2 dx

lim

1, интеграл сходится;

1 x

cos xdx

lim

cos xdx

lim sin x

lim sina ,

интеграл расходится, так как

при a

предел

lim sin a не существует;

b dx

, интеграл расходится.

lim

limlnb

1 x

ТЕОРЕМА 3 (признак сравнения). Если на промежутке a;

непрерывные

функции

удовлетворяют условию 0

x , то из сходимости ин-

теграла

x dx следует сходимость интеграла

f x dx, а из расходимости инте-

грала

x dx следует расходимость интеграла

x dx .

Пример. Сходится ли интеграл

1 x 2 1

При x

1 имеем

. Но интеграл 1

сходится. Следовательно, ин-

x 2

1 3x

x 2

теграл

также сходится (и его значение меньше 1).

x 2

ТЕОРЕМА 4.

Если существует предел

lim

k , 0 k

( f x 0 и

0 ), то интегралы

x dx и

x dx одновременно сходятся или оба расхо-

дятся (т. е. ведут себя одинаково в смысле сходимости).

Пример. Исследовать сходимость интеграла

dx .

Интеграл

сходится,

так

как

интеграл

сходится и

x 2

ln 1

lim

1 .

2. Интеграл от разрывной функции (несобственный интеграл II рода)

Пусть функция f x непрерывна на промежутке			a; b			и имеет бесконечный
				b
разрыв при x b . Если существует конечный предел lim					f	x dx , то его называют
			0	a
				a
			b
несобственным интегралом второго рода и обозначают				f	x dx .
			a
Таким образом, по определению,
b		b
f x dx	lim f x dx .					(3.4)
a	0	a
a		a
						b
Если предел в правой части существует,	то несобственный интеграл f x dx схо-

дится. Если же указанный предел не существует или бесконечен, то говорят, что

интеграл f x dx расходится.

a
Аналогично, если функция f x терпит бесконечный разрыв в точке x		a , то пола-
гают:
b	b
f x dx	lim f x dx .	(3.5)
a	0 a

Если функция f x терпит разрыв во внутренней точке c отрезка			a; b , то несобст-
венный интеграл второго рода определяется формулой:
b	c	b
f x dx	f x dx	f x dx .	(3.6)
a	a	c

В этом случае интеграл слева называют сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.

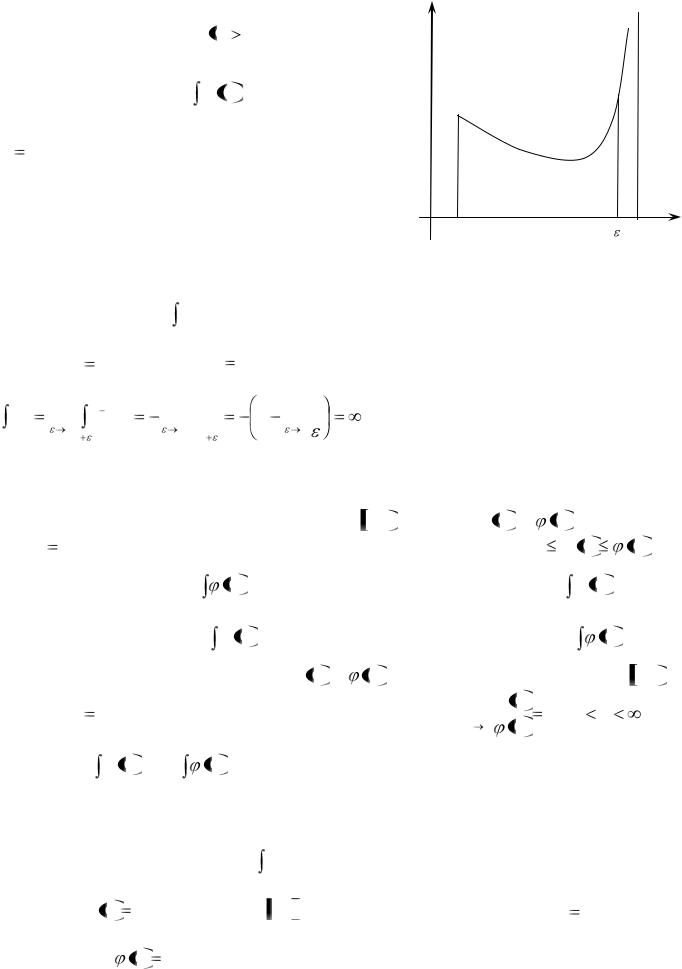
В случае, когда f x 0 , несобственный

		b
интеграл второго рода			f x dx	(разрыв в точке
		a
x b ) можно	истолковать геометрически как
площадь бесконечно		высокой		криволинейной
трапеции	(см. рис. 4).
	1	dx
Пример. Вычислить			.
Пример. Вычислить		x 2	.
	0	x 2

y=f(x)

0 a	B -	b	x
			x

Рис.4

При x

функция

терпит бесконечный разрыв;

x 2

1 dx

lim

1 x 2 dx

lim

, интеграл расходится.

0 x2

0 0

0 x

Сформулируем признаки сходимости для несобственных интегралов второго

рода.

ТЕОРЕМА 5. Пусть на промежутке

a; b функции f x и

непрерывны,

при x

b терпят бесконечный разрыв и удовлетворяют условию 0

x . Из

сходимости интеграла

x dx

вытекает сходимость интеграла

x dx , а из

расходимости интеграла

f x dx вытекает расходимость интеграла

x dx .

ТЕОРЕМА 6. Пусть функции f

x и

x непрерывны на промежутке

a; b и

в точке x

b терпят разрыв. Если существует предел lim

f x

k ,

, то

x b

интегралы

x dx и

x dx одновременно сходятся или одновременно расходят-

ся.

Пример. Сходится ли интеграл

sin x

Функция

имеет на 0;1

единственный разрыв в точке x

0 . Рассмот-

sin x

рим функцию

. Интеграл

1 dx

lim

limln x

0 limln

0 x

0 0

расходится. И так как

lim

1 ,

sin x

x 0

то интеграл

также расходится.

sin x

УПРАЖНЕНИЕ 3

Вычислить несобственные интегралы или доказать их расходимость:

1		dx						e 2 x dx						4
1)				;		3)				;		5)			ctg5xdx;
1)		1 3x2		;		3)	0 e 2 x		1	;		5)	0		ctg5xdx;
													0
		dx					3		dx				2			dx
		dx							dx			6)				dx
2) e					;	4)					;		1				.
	x(ln x		5 )					x2	4 x	4
	x(ln x		5 )				2	x2	4 x	4						4 x2

IV. Геометрические приложения определенного интеграла

1.Вычисление площадей плоских фигур

Выше было показано, что определенный интеграл от неотрицательной непрерывной функции равен площади соответствующей криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла, на чем и основано его применение к вычислению площадей плоских фигур.

Как было установлено ранее, площадь криволинейной трапеции, т. е. фигуры, ограниченной графиком неотрицательной непрерывной функции y=f(x), х [а; b], отрезком [а; b] оси абсцисс и отрезками прямых х=а, x=b (a<b), вычисляется по формуле:

		b
	S	f	x dx.	(4.1)
		a
Пример.	Вычислить площадь плоской		фигуры, ограниченной	линиями
y 3x2 6x	5, х = -11, х = 2 и отрезком [-1; 2] оси абсцисс.

Данная фигура представляет собой криволинейную трапецию (она заштрихована на рис. 5), поэтому ее площадь вычисляется по формуле (4.1):

	2	2		2		2
S	3x2 6x 5 dx x3	2	3x2	2	5x	2	1	15.
		1			1
		1			1

Пусть теперь y=f(x), х [а; b],- неположительная непрерывная функция. График

такой функции расположен под осью абсцисс (рис. 6), и значит, f x dx 0 .

aA B b

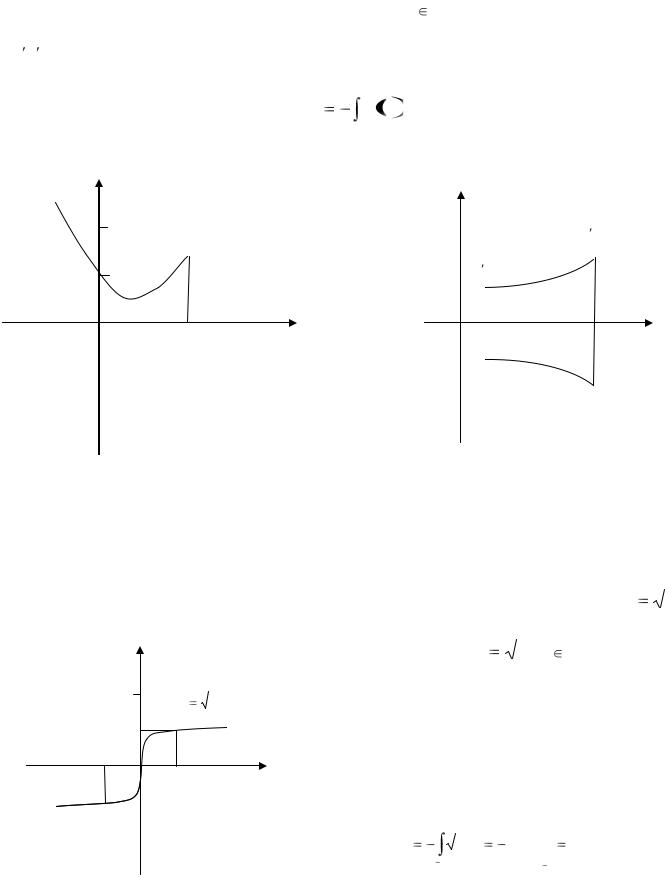
Рассмотрим вспомогательную функцию y=-f(x), х [а; b], являющуюся неотрицательной непрерывной функцией. Следовательно, площадь криволинейной трапеции aA B b , ограниченной графиком функции y=-f(x), и отрезком [а; b] оси абсцисс и отрезками прямых x=a, x=b (a<b) (рис. 6), можно вычислить по формуле (4.1), т. е.

						b
					S	f x dx			(4.2)
						a

	y
							y	B
							y

		5					A	y=-f(x)
							A

	0				x		0 a	b	x

-1
		1		2
		1		2
							A
								y=f(x)
								B
			Рис. 5					Рис. 6

График функции y=-f(x) симметричен графику функции y=f(x) относительно оси абсцисс, поэтому фигуры аАВb и равны, а значит, имеют равные площади. Таким образом, площадь плоской фигуры аАВb также вычисляется по форму-

ле (4.2).


Пример.		Вычислить площадь плоской фигуры, ограниченной линиями y 5 x ,
х=-1 и осью абсцисс (рис. 7).
											5
			y				График функции y				5		x ,			х [-1; 0] распо-
			y
		2					ложен под осью Ох, поэтому для вычисления
		2		y	5 x		ложен под осью Ох, поэтому для вычисления
		1					площади данной		плоской					фигуры применим
		1



				1		2 x	формулу (4.2):
	-2 -			1		2 x	формулу (4.2):

			-1				0								6	0
			-1

			-2					5			5					5
											5				5	5

							S			xdx		6 x				6 .
							S			xdx		6 x				6 .
							1									1
			Рис. 7

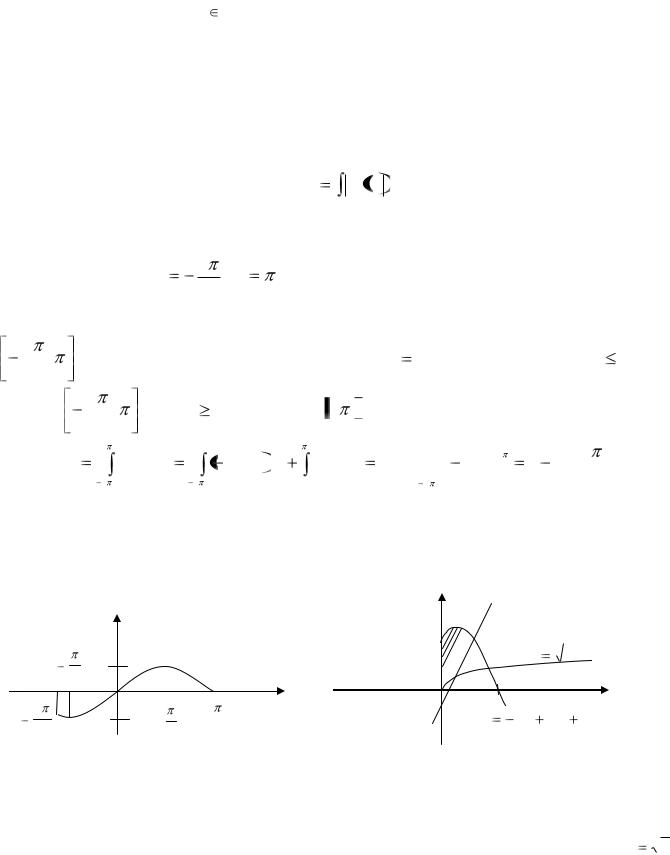
Пусть далее y=f(x), x [a; b] — непрерывная на отрезке [a; b] функция, график

которой пересекает отрезок [a; b] оси абсцисс в конечном числе точек. Используя

формулы (4.1) и (4.2), получим, что площадь плоской фигуры, ограниченной графи-

ком функции y=f(x), отрезком [a; b] оси абсцисс и отрезками прямых х=а, х=b, вы-

числяется по формуле:

	b
S	f x dx .	(4.3)

Пример. Вычислите площадь плоской фигуры, ограниченной графиком функции

f(x)=sinх, прямыми x	4	, x	, а также осью абсцисс (рис. 8).
	7

Решив уравнение sinx=0, заключаем, что график функции f(x)=sinx на отрезке

;

пересекает ось абсцисс в одной точке x

0. Таким образом, sin x 0 на

отрезке

; и sin x 0 на отрезке 0, . Воспользуемся формулой (4.3):

sin x

sin x dx

sin xdx cos x

cos x

3 cos

4 / 7

Если требуется вычислить площадь плоской фигуры более сложного вида, то эту фигуру разбивают на сумму нескольких криволинейных трапеций. Затем искомую площадь находят как алгебраическую сумму площадей этих криволинейных трапеций.

		y
	2	1
	2
4		-1
		-1

	y				y = 2x-1
	4				y = 2x-1
	4
	3					3
	3				y	3	x
y = sin x	2				y		x
	2

	1

x	0	1	2		3			3 x
x	0			y	x 2	2x		3 x

7	2
	Рис. 8	Рис. 9

Пример. Вычислить площадь плоской фигуры, ограниченной линиями y 3 x , у=2х-1, y=-x2 + 2x+3 и осью ординат (рис. 9).

Для нахождения площади данной фигуры воспользуемся последним заме-

чанием:

	2							2						1
	S	x2		2x	3 dx			2x		1 dx				3 xdx
	0							1						0
			3				2		2	4			1


		x		x2 3x				x2 x			3				55
		x									3	x 3			55	.
		3					0		1	4		x 3	0	12		.
		3							1	4				12



Теперь	рассмотрим	плоскую				фигуру,			ограниченную графиком функции
r f ,	; , заданной в полярной системе координат, и отрезками лучей																,

(рис. 10). Будем называть такую фигуру криволинейным сектором, площадь которого можно вычислить по формуле (4.1), однако удобнее вывести специальную формулу.

r = f (x)

i-1

Рис. 10

Разобьем отрезок

; точками

, i

0,1, ...,n,

на n равных по длине от-

резков

;

1 ,

2 , …, n 1;

, в каждом из которых выберем некоторую точку

сi

i 1;

, i

1, ...,n.Составим интегральную сумму

r 2 c

...

r 2

1 n

r 2

(4.4)

2 i 1

где

i 1 . Каждый член суммы (4.4)

равен площади кругового сектора

(рис. 10), а вся сумма равна площади соответствующей ступенчатой фигуры. Так как для непрерывной функции r r , ; 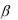, предел интегральных сумм (4.4) при

n 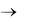существует, то для вычисления площади криволинейного сектора SOAB получим следующую формулу:

(рис. 11).

Искомая площадь в 4 раза больше площади заштрихованной части на рис.11. Поэтому, используя формулу (4.5), находим:

	1	/ 4	/ 4		/ 2		/ 2

S 4		cos2	d	cos2 d 2	cosu du sinu	0		1.
	2
		0	0		0

AM1M 2 ...M n 1B,

Пример. Вычислить площадь «трехлепестковой розы» r a cos 3 .

Искомая площадь в 6 раз больше площади, заштрихованной на рис. 12. Согласно формуле (4.5), получим:

	1	/ 6			/ 6		/ 2 1	cos 2u		a	2
S 6			a2 cos 2 3 d	a2	cos 2 3 d 3	a2			du			.
S 6	2		a2 cos 2 3 d	a2	cos 2 3 d 3	a2		2	du	4		.
	2	0			0		0	2		4

y		y
y
	4	6
		6
	x	x
	x	r a cos3
r	cos2	r a cos3
r	cos2
Рис. 11		Рис. 12

2. Вычисление длин дуг плоских кривых

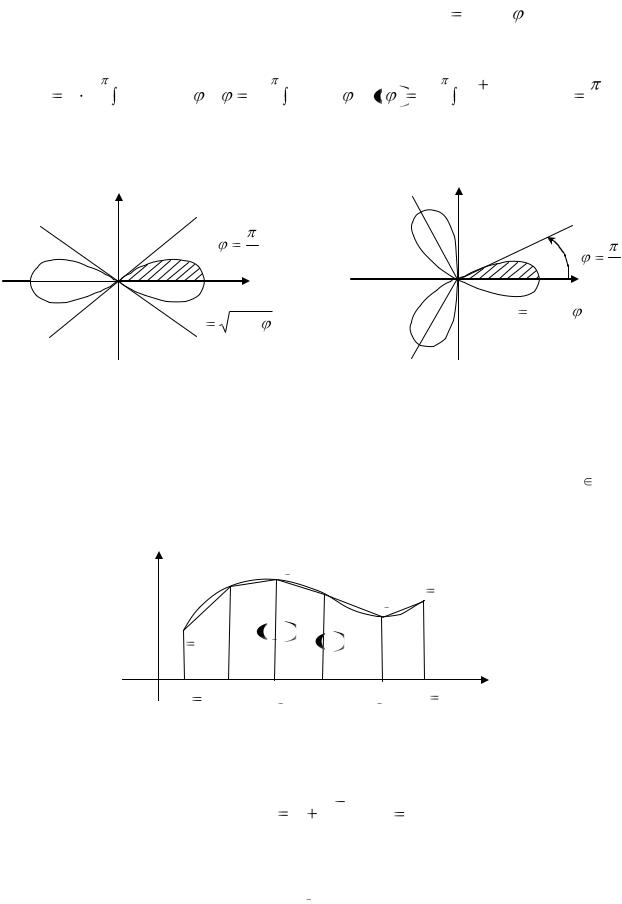
Пусть дана плоская кривая АВ (рис. 13), уравнение которой y=f(x), х [а; b], где f(x)-непрерывно дифференцируемая функция на отрезке [а; b].

y		M 1		M i 1		M i
						M i	M n	B
						M n	M n	B
						M n	1
M 0		A	f	xi 1	f	xi
M 0		A			f	xi
0 x	0	a x1		xi 1		xi xn 1	xn	b x
	0

Рис. 13

Разобьем отрезок [а; b] точками	x a	b a	i, i 0,1, ..., n, на n частей равной дли-

	i	n

ны. Через точки деления хi проведем прямые, параллельные оси ординат Оу. Точки пересечения этих прямых с кривой АВ обозначим через Mi. Соединив эти точки хордами, получим ломаную вписанную в кривую АВ. Пусть периметр

этой ломаной равен Рn.

Длиной дуги АВ будем называть число l, равное пределу последовательности

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.09.2019271.76 Кб12вопросы геодезия.docx
#
29.03.2015140.25 Кб42Вопросы жбк.pdf
#
18.04.2019417.79 Кб2ВОПРОСЫ_экз_2.doc
#
24.11.201911.3 Mб17ВОС ОБОР. Бондарь.doc
#
23.09.2019991.96 Кб3вышка - 2003.docx
#
29.03.20152.37 Mб12Вышка задачи.pdf
#
29.03.2015683.01 Кб69Вяжущие вещества Цемент кислотостйкая.doc
#
29.08.2019175.54 Кб9Газовые сети.docx
#
29.03.201536.78 Кб18генплан.docx
#
29.03.201514.04 Кб26Геодезия.docx
#
28.09.20197.18 Mб73ГЕОЛОГИЯ!.docx