
Вышка задачи
.pdf
периметров Pn :
l lim Pn .
n
Выведем формулу для вычисления длины дуги. Для этого сначала найдем периметр ломаной AM1M 2 ...M n 1B, . Точка Mi-1 с координатами xi-1 f xi 1  и точка Mi с ко-
и точка Mi с ко-
ординатами xi и f xi являются концами i-ro звена ломаной. Длину i-ro звена вычислим по формуле расстояния между двумя точками плоскости:
l |
x |
x |
2 |
f |
x |
f |
x |
2 . |
(4.6) |
i |
i |
i 1 |
|
i |
|
i 1 |
|
|
|
Учитывая, что f(х) — непрерывно дифференцируемая функция на отрезке |
[а; b], по |
||||||||
формуле Лагранжа будем иметь: |
|
|
|
|
|
|
|
|
|
f |
xi |
f |
xi 1 |
f |
ci |
xi |
xi 1 |
, |
(4.7) |
где сi — некоторая точка интервала xi 1; xi . Подставив выражение (4.7) в формулу (4.6), получим:
|
l |
1 |
|
f |
c |
2 |
x , |
|
|
(4.8) |
||
|
i |
|
|
|
i |
|
i |
|
|
|
|
|
где xi xi xi 1. Значит, периметр ломаной |
AM1M 2 ...M n 1B равен следующей |
|||||||||||
сумме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
n l |
n |
|
|
|
|
|
|
|
|
|
|
P |
1 |
f |
c |
2 |
|
x . |
|
|
||||
n |
|
i |
|
|
|
i |
|
|
i |
|
|
|
i |
1 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Итак, мы получили интегральную сумму для непрерывной функции 1 f c |
2 на |
|||||||||||
|
|
|
|
|
|
|
|
|
|
i |
||
отрезке [а; b]. Так как предел этой суммы при n 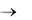 существует, то, согласно определению, находим:
существует, то, согласно определению, находим:
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
lim P |
|
lim |
1 |
|
|
f |
c |
2 x |
|
|
|
1 |
|
f x |
2 dx . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
n |
|
n |
|
|
i |
1 |
|
|
|
|
|
|
|
i |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 dx . |
|
|
|
|
|
|
|
|
(4.9) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
1 |
f |
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. Вычислить длину дуги параболы y |
|
1 |
x |
2 |
от ее вершины А(0; 0) до точки |
|||||||||||||||||||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В |
1; |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для вычисления длины дуги воспользуемся формулой (4.9). Так как y x , то |
|||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
1 x2 dx . Так как |
|
1 |
|
|
x2 dx |
|
|
1 |
x2 |
|
|
|
ln |
x |
1 |
|
x2 |
|
C , то |
|||||||||||||||||||||||||
0 |
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ln 1 2 |
|
|||||||||||||
|
|
1 x2 dx |
|
x 1 x2 |
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
. |
|||||||||||||||||||||||||||||
|
|
|
|
l |
|
|
|
ln x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Если уравнения кривой АВ задано в параметрической форме |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x t , |
|
|
t |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
y t , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
23

где x t |
|
и y t |
- |
непрерывные функции с непрерывными производными и x |
a , |
||||||||||||||||||||||||||||||||||
x |
|
b , то длина l кривой АВ находится по формуле |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
x |
t |
|
2 |
y |
|
x |
2 dt . |
|
|
(4.10) |
|||||||||
Формула (4.10) может быть получена из формулы (4.9) |
подстановкой |
x |
x t |
, |
|||||||||||||||||||||||||||||||||||
dx |
x |
t dt , |
f |
|
x |
|
|
y |
|
t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример. Найти длину окружности радиуса R. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Найдем |
1 |
|
часть еѐ длины от точки (0; R) до точки |
y |
|
|
|
|||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(R;0) (см рис. 14). Так как y |
|
|
R 2 |
|
x2 , то |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
R |
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
0 |
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
4 l |
0 |
1 |
|
R2 |
|
x2 dx |
R arcsinR |
|
0 |
R |
2 . |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Значит, l 2 R . Если уравнение окружности записать в |
|
|
|
|
|||||||||||||||||||||||||||||||||||
параметрическом виде x |
Rcost , |
y |
R sin t |
0 |
|
t |
2 , |
|
|
|
|
||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 14 |
|
|
|
то |
|
|
|
|
R sint 2 |
|
R cost 2 dt |
|
|
|
|
|
|
|
2 R . |
|
|
|
|
|
|
|
|
||||||||||||||||
l |
|
|
|
|
|
Rt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пусть |
кривая |
АВ |
задана |
уравнением |
|
в |
полярных |
координатах |
r |
r |
, |
|||||||||||||||||||||||||||
|
|
|
|
. Предположим, что r |
и r |
|
|
|
непрерывны на отрезке ; . |
|
|
|
|||||||||||||||||||||||||||
|
Если в равенствах x |
|
r cos |
, y |
r sin |
, |
связывающих полярные и декартовы |
||||||||||||||||||||||||||||||||
координаты, параметром считать угол , то кривую АВ можно задать параметриче-
ски |
x |
r |
cos |
, |
Тогда |
x |
r |
|
|
|
cos |
|
r |
sin |
, |
Поэтому |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
y |
r |
sin . |
|
|
|
y |
r |
|
|
|
sin |
|
r |
cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
y 2 |
|
|
|
|
|
r |
|
cos |
r |
|
|
sin |
2 |
|
r |
sin |
|
r |
cos |
2 |
|
r |
2 |
r |
2 . |
||||||||||
Применяя формулу (4.10), получаем l |
|
|
r 2 |
r 2 d . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
Пример. Найти длину кардиоиды r |
a 1 |
cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Кардиоида r |
a 1 |
cos имеет вид, изображенный на рис. 15. Она симметрична |
|
|
||||||||||||||||||||||||||||||||||
относительно полярной оси. Найдем половину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
длины кардиоиды: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
a 1 |
|
cos |
2 |
a |
sin |
|
2 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a |
2 |
2cos d |
a |
2 |
|
d |
|
2a cos |
|
d |
4a |
sin |
|
|
|
|
4a. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
0 |
|
|
|
|
|
1 |
|
|
0 |
|
|
2 |
|
|
|
|
0 |
2 |
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Таким образом, |
l |
4a . Значит, |
l |
8a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 15 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
24
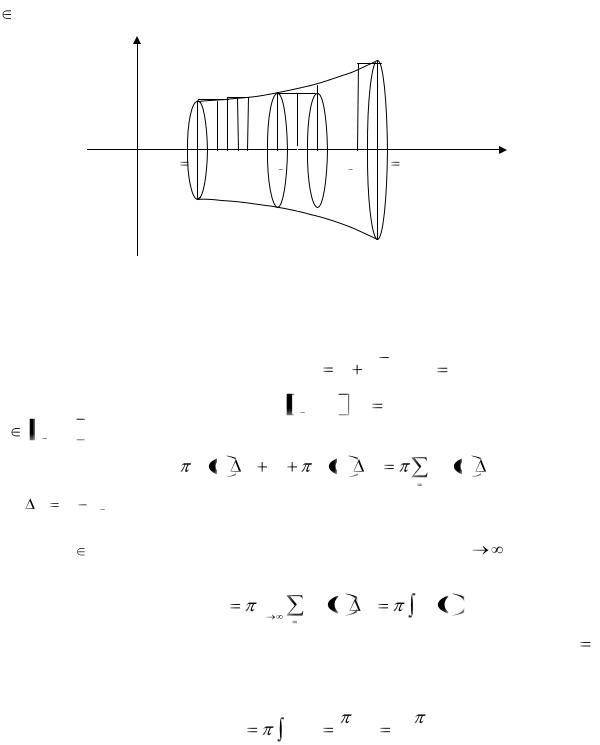
3. Вычисление объемов тел вращения
Рассмотрим тело, образованное вращением вокруг оси Ох криволинейной трапеции аАВb, ограниченной графиком неотрицательной непрерывной функции f(х), х [а; b], осью абсцисс и отрезками прямых х = а, х = b (рис. 16).
y |
B |
|
|
|
A |
x0 a x1 x2 xi 1 сi xi xn 1 xn b |
x |
||
|
|
|
|
|
|
|
|
Рис. 16 |
|
|
|
|
|
|
|
|
|
|
|
Разобьем отрезок [а; b] точками |
x |
a |
|
b |
a |
i , |
i |
0,1,..., n |
на n частей равной |
||||
|
|
|
|
|||||||||||
|
|
|
|
|
i |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
длины. |
На |
каждом из отрезков xi |
1 ; xi , |
i |
1,..., n |
выберем |
некоторую точку |
|||||||
ci |
xi 1; xi |
и составим интегральную сумму: |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
f 2 c |
x ... |
f 2 |
c |
x |
|
|
|
f 2 c |
x , |
(4.12) |
|
|
|
|
1 |
i |
|
n |
|
n |
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
где |
xi |
xi |
xi 1 . Каждый член суммы (4.12) равен объему кругового цилиндра, а вся |
|||||||||||
сумма равна объему соответствующего ступенчатого тела. Для непрерывной функ-
ции f(x), х [а; b], предел интегральных сумм (4.12) при n |
существует и равен |
|||||
объему V рассматриваемого тела вращения: |
|
|
|
|||
|
|
n |
|
|
b |
|
V |
lim |
|
f 2 c |
x |
f 2 x dx . |
(4.13) |
|
n |
|
i |
i |
|
|
|
i |
1 |
|
a |
|
|
|
|
|
|
|||
Пример. Вычислить объем тела, образованного вращением параболы y x2 вокруг
оси абсцисс на участке от х=0 до x=2. Используя формулу (4.13), находим
|
2 |
x5 |
|
|
2 |
32 |
|
|
|
|
|||||
V |
x4dx |
|
|
|
|
|
. |
5 |
|
|
|
5 |
|||
|
0 |
|
|
0 |
|
||
|
|
|
|
|
|
Если тело образовано вращением криволинейной трапеции, ограниченной графиком функции х=φ(y), осью ординат и отрезками прямых y=а и y=b, то объем полученного тела вращения будет вычисляться по формуле:
25

|
b |
|
V |
2 ( y)dy . |
(4.14) |
a
4. Вычисление площадей поверхностей тел вращения
Найдем площадь поверхности, полученной в результате вращения кривой АВ вокруг оси абсцисс (см. рис. 16). Пусть функция y=f(x), х [а; b] непрерывно диффе-
ренцируема на отрезке [а; b]. Через точки |
x a |
b a |
i , i 0,1,..., n проведем пря- |
|
|||
|
i |
n |
|
|
|
||
мые, параллельные оси ординат Оу, а их точки пересечения с кривой АВ обозначим через Мi. Соединив эти точки хордами, получим ломаную AM1M 2 ...M n 1B . При ее
вращении вокруг оси абсцисс получается поверхность, которая состоит из боковых поверхностей усеченных конусов, образованных вращением звеньев ломаной AM1M 2 ...M n 1B . Пусть площадь этой поверхности равна Sn.
Площадью поверхности тела вращения будем называть число S, равное пределу последовательности площадей {Sn}:
S lim Sn .
n
Площадь поверхности ломаной AM1M 2 ...M n 1B выражается следующим образом:
|
n |
|
f xi 1 |
f xi |
|
n |
|
|
|
|
|
|
|
S |
2 |
l |
f x |
f x |
1 f c |
2 x , |
(4.15) |
||||||
n |
|
|
i |
||||||||||
|
|
|
2 |
|
i 1 |
i |
i |
|
i |
|
|||
|
i 1 |
|
|
i 1 |
|
|
|
|
|
|
|||
где мы воспользовались формулой (4.8). Сумма (4.15) не является интегральной суммой для функции
|
|
|
|
|
|
|
2 f |
x |
1 |
|
|
f |
c |
2 |
, |
|
|
|
|
(4.16) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||
так как в слагаемом, соответствующем отрезку |
xi 1 ; xi |
, фигурируют несколько то- |
|||||||||||||||||||||
чек этого отрезка, а именно xi 1 , |
xi , сi . Однако можно доказать, что предел суммы |
||||||||||||||||||||||
(4.15) равен пределу интегральной суммы для функции (4.16), т. е. |
|||||||||||||||||||||||
|
|
|
|
|
|
n f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
lim S |
n |
lim |
x |
1 |
|
|
f |
x |
|
1 |
|
|
f c |
2 |
x |
||||||
|
|
n |
|
n |
i 1 |
i |
|
|
|
i |
|
|
|
|
|
|
i |
|
i |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n f c |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x 2 dx. |
|||||
2 |
lim |
1 |
f |
c |
|
x |
2 |
|
|
f |
x |
1 |
f |
||||||||||
|
n |
i |
1 |
i |
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 dx. |
|
(4.17) |
||||||
|
|
|
|
|
S |
2 |
f |
x |
1 |
f |
|
x |
|
||||||||||
a
Пример. Вычислить площадь поверхности параболоида, образованного вращением
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дуги параболы y |
x , х |
[0; 2] вокруг оси абсцисс. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Для вычисления площади поверхности воспользуемся формулой (4.17). Так |
||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
9 |
|
|
|
3 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
13 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
как f x |
|
|
|
, то S 2 |
|
x 1 |
dx |
1 4xdx |
|
|
udu |
|
u 2 |
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 |
|
x |
|
|
0 |
|
|
|
4x |
0 |
|
|
4 |
1 |
|
|
6 |
|
|
|
|
1 |
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26

УПРАЖНЕНИЕ 4
1. Вычислите площадь плоской фигуры, ограниченной линиями:
а) y 6x x2 , y 0 ; |
|
|
|
|
|
|
б) y2 |
4x 0 ; x y 0 |
|||||||||
в) y 2x 16 , y 8 7x x2 , x 0 ; |
г) y x3 , x y 2 , y 0 ; |
||||||||||||||||
д) y |
arсsin x , x |
1 |
, y |
0 ; |
|
|
|
|
|
е) y ln x , y 0 , x e , x e2 . |
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
2. Вычислите площадь плоской фигуры, ограниченной линиями: |
|||||||||||||||||
а) r |
a(1 cos |
) ; |
|
|
б) r |
|
a |
, |
|
|
2 . |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||
3.Вычислите длину дуги кривой: |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а) y |
|
x3 , x |
0;1 ; |
|
|
б) y |
ln x, x |
3; |
8 . |
||||||||
4. Вычислите объем тела, образованного вращением вокруг указанной оси фигуры, ограниченной линиями:
а) xy |
4, x |
1, x |
4, y 0 (Оx); |
б) ( y a)2 |
ax, x 0, y 2a (Оx); |
||
в) y x3 , x 0, y 8 (Оy); |
|||
г) y |
1 |
, x |
1, x 1, y 0 (Oy). |
|
|||
1 x2 |
|||
5. Вычислите площадь поверхности, образованной вращением вокруг оси абсцисс кривой:
а) x2 y2 R2 ;
б) дуги кривой y2 4 x, отсеченной прямой x 2 .
V. Приложения определенного интеграла к решению физических задач
1.Задача о вычислении пути
Пусть материальная точка движется прямолинейно с некоторой скоростью v v(t) . Требуется найти путь, который пройдет эта точка за промежуток времени
от t a до t b.
В простейшем случае, когда скорость постоянна, т. е. v(t) v0 const , путь,
пройденный точкой, равен (по определению, известному из курса физики) произведению скорости на время движения:
S v0 (b a).
27
В общем случае, когда скорость непостоянна, поступают следующим об-
разом. |
Промежуток времени |
a;b |
разбивают точками t0 a,t1 , ..., tn 1 ,tn b |
||
( t0 t1 |
... tn )на n отрезков одинаковой длины |
(рис. 17). Длина каждого отрезка |
|||
равна |
|
|
|
|
|
|
ti ti |
ti 1 |
b a |
, i |
1, 2, ..., n. |
|
|
||||
|
|
|
n |
|
|
|
с1 |
|
|
сi |
|
сn |
0 |
a t0 |
t1 |
ti 1 |
ti |
tn 1 |
b tn |
Рис. 17
Выбрав на каждом отрезке ti 1 ;ti  произвольную точку ci,составляют сумму:
произвольную точку ci,составляют сумму:
|
n |
|
|
v(ci ) ti . |
(5.1) |
|
i 1 |
|
Каждое слагаемое этой суммы дает приближенное значение пути, пройденно- |
||
го материальной точкой за время от t |
ti 1 до t |
ti . Следовательно, весь путь, прой- |
денный точкой за время от t a до t |
b , приближенно выражается суммой (5.1). |
|
Это приближение будет тем лучше, чем мельче отрезки разбиения. Поэтому путь s,
пройденный точкой за отрезок времени |
a;b , определяется пределом суммы (5.1) |
|
при n |
: |
|
|
|
n |
|
s lim |
v(ci ) ti . |
|
n |
i 1 |
|
|
|
Как известно (см. п.1 § 1), этот предел есть определенный интеграл от функции v(t) на отрезке a;b . Таким образом, путь s, пройденный за отрезок времени от t a до t b материальной точкой, движущейся прямолинейно со скоростью v(t), вычисляется по формуле:
s
Пример. Тело движется прямолинейно путь, пройденный телом за первые 3 с.
Используя формулу (5.2), получим
|
3 |
s |
3t 2 4t 1dt |
|
0 |
b |
|
v(t)dt. |
(5.2) |
a |
|
со скоростью v t |
3t 2 4t 1 (м/с). Найти |
t3 2t 2 t |
|
3 |
48 м . |
|
|||
|
|
0 |
|
|
|
Пример. Определить, на какую максимальную высоту поднимется камень, брошенный от поверхности Земли вертикально вверх со скоростью v0 , если не учитывать
сопротивление воздуха.
В этом случае скорость камня равна v t v0 
28
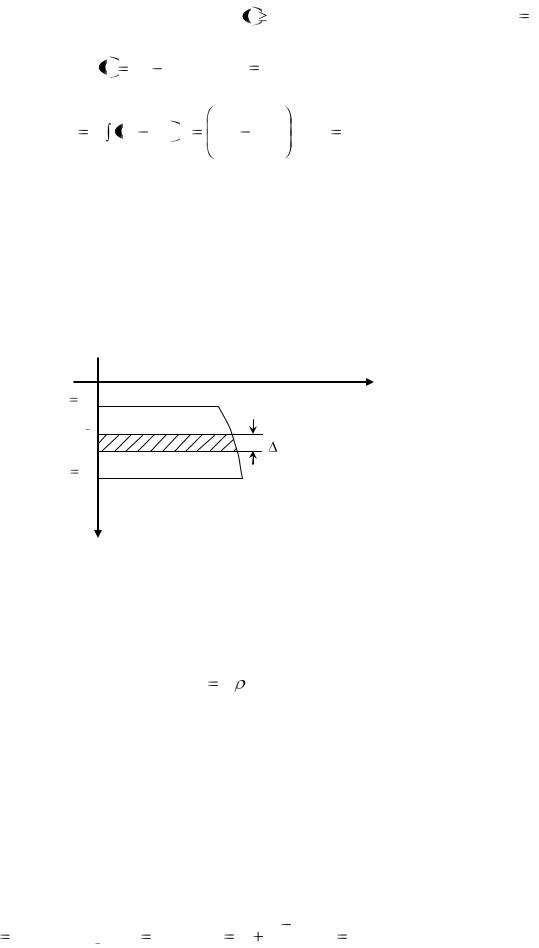
падения. Камень будет лететь вверх, |
пока v t |
|
|
0 |
, т. е. до момента времени t |
v0 |
. |
|||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
Положив в формуле (5.2) |
v t v |
gt , a=0, b |
|
v0 |
|
, получим: |
|
|
|
|||||
|
|
|
|
|
|
|||||||||
|
0 |
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
v0 / g |
|
|
gt |
2 |
|
|
v0 |
/ g |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
s |
v0 |
gt dt |
v0t |
|
|
|
|
|
v0 |
. |
|
|
||
2 |
|
|
|
|
2g |
|
|
|||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.Задача о силе давления жидкости
Пусть пластина в виде криволинейной трапеции погружена вертикально в жидкость с плотностью 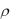 так, что ее боковые стороны параллельны поверхности жидкости и находятся ниже ее уровня соответственно на расстояниях а и b (рис. 18). Требуется определить силу давления жидкости на пластину.
так, что ее боковые стороны параллельны поверхности жидкости и находятся ниже ее уровня соответственно на расстояниях а и b (рис. 18). Требуется определить силу давления жидкости на пластину.
|
0 |
|
y |
|
x0 |
a |
f(x) |
||
|
||||
|
xi 1 |
|
|
|
|
xi |
|
xi |
|
xn |
b |
|
|
x
Рис. 18
Если пластина находится в горизонтальном положении на глубине h от поверхности жидкости, то сила давления Р жидкости (в ньютонах) на нее будет равна весу столба жидкости, имеющего основанием данную пластину, а высотой — глубину h, т. е.
P g hS , |
(5.3) |
где g-ускорение силы тяжести, S-площадь пластины.
Если же пластина погружена в жидкость вертикально, то по формуле (5.3) силу давления жидкости на нее вычислить нельзя, так как в этом случае давление жидкости на единицу площади пластины изменяется с глубиной погружения, т. е. зависит от расстояния площадки до поверхности жидкости.
При решении задачи будем учитывать тот факт, что, по закону Паскаля, давление в жидкости передается одинаково во всех направлениях, в том числе и на вертикальную площадку.
Разобьем пластину на n частей (малых горизонтальных полосок) прямыми, параллельными поверхности жидкости (т. е. параллельными оси Оу) и проходящими
через точки |
x |
a , |
x , ..., x |
, x |
|
b где |
x a |
b a |
i, i 0,1, 2, ..., n. |
|
n |
|
|||||||||
|
0 |
|
1 |
n 1 |
|
|
1 |
n |
||
|
|
|
|
|
|
|
|
|
||
29
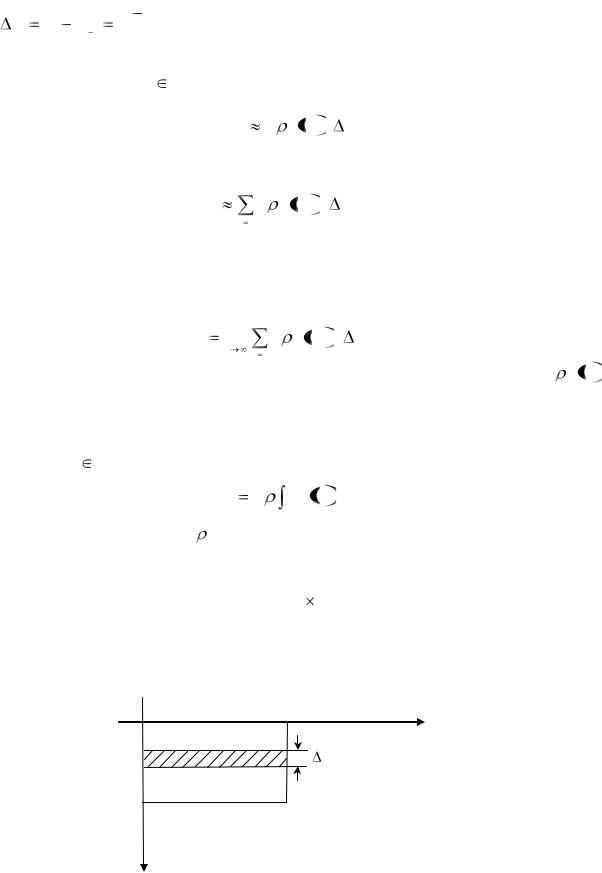
Выделим одну из полосок (на рис. 18 она заштрихована), находящуюся на глубине xi . Для достаточно узкой полоски давление во всех ее частях можно считать
приближенно одинаковым, а саму полоску можно принять за прямоугольник с вы-
сотой |
x |
x |
x |
b a |
и основанием, равным нижнему основанию полоски. |
|
|||||
|
i |
i |
i 1 |
n |
|
|
|
|
|
||
Очевидно, что длина основания прямоугольника является функцией от х. Обозначим эту функцию через f(х), х [а; b]. Значит, силу давления Р на i-ю полоску можно приближенно вычислить по формуле (5.3), т. е.
Pi g f xi xi xi . |
(5.4) |
Просуммировав силы давления жидкости на все полоски, найдем приближенное значение силы давления жидкости на всю пластину:
n
P g f xi xi xi .
i 1
Точность приближенного равенства тем больше, чем мельче отрезки, на которые разбит отрезок [а; b].
Следовательно, точное значение силы давления жидкости на пластину определяется по формуле:
|
n |
|
P lim |
|
g f xi xi xi . |
n |
i |
1 |
|
Как известно, этот предел есть определенный интеграл от функции g f x на
отрезке [а; b].
Таким образом, сила давления Р жидкости на вертикально погруженную в нее пластину, имеющую форму криволинейной трапеции, соответствующей графику функции у=f(x), х [а; b], вычисляется по формуле:
b |
|
P g x f x dx , |
(5.5) |
a
где g-ускорение силы тяжести, -плотность жидкости.
Пример. Аквариум имеет форму прямоугольного параллелепипеда. Найти силу давления воды (плотность воды 1000 кг/м3) наполняющей аквариум, на одну из его вертикальных стенок, размеры которых 0,4 м 0,7 м.
Выберем систему координат так, чтобы оси Оу и Ох соответственно содержали верхнее основание и вертикальную стенку аквариума (рис. 19). Для нахождения силы давления воспользуемся формулой (5.5).
0 0,7
y
xi
0,4
x
Рис.
30
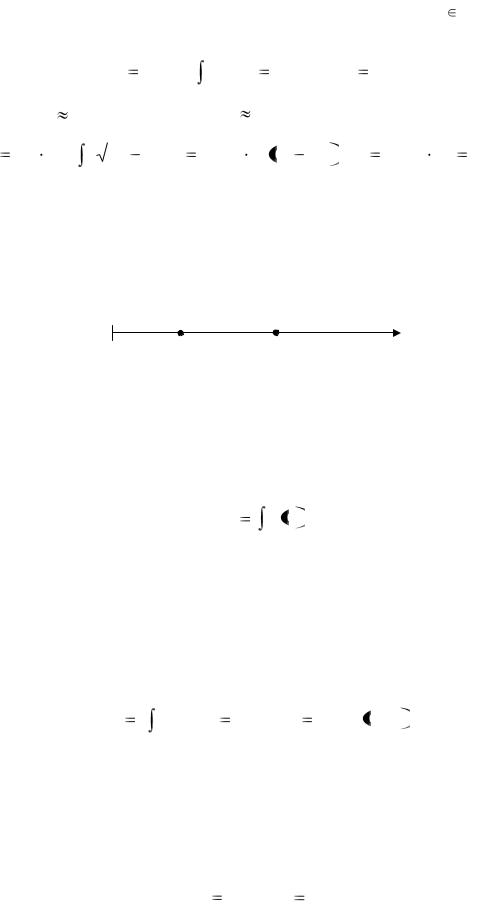
Стенка имеет форму прямоугольника, поэтому f(х)=0,7, х [0; 0,4], пределы интегрирования а=0 и b=0,4. Следовательно,
|
|
|
|
0,4 |
|
|
|
x2 |
|
|
0, 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
P |
1000g |
0,7xdx |
700g |
|
|
|
|
|
|
56g. |
|||
|
2 |
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
||
Учитывая, что g 9,8 м/с2 , получаем P |
548,8 H. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||
5 |
|
|
|
|
2 |
|
|
|
3 / 2 |
|
0 |
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
P 2g 900 x 52 |
x 2 dx |
900 g |
52 x 2 |
|
600 g 53 75000 g. |
|||||||||
3 |
|
|
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
5 |
||
|
|
|
|
|
|
|
|
|
|
|
||||
3. Работа переменной силы
Пусть материальная точка движется вдоль оси Ох под действием переменной силы f(х). Требуется найти работу, затраченную на перемещение материальной точки из положения М(а) в положение М(b) (рис. 20).
M(a) |
M(b) |
0 |
x |
a |
b |
Рис. 20
С этой задачей мы уже встречались при определении понятия определенного интеграла (см. п. 1 в главе I). Поэтому, опуская промежуточные рассуждения, сразу запишем формулу для вычисления работы:
|
b |
|
A |
f x dx . |
(5.6) |
a
Пример. Какую работу надо затратить, чтобы растянуть пружину на 0,05 м, если сила в 1 Н растягивает ее на 0,01 м?
По закону Гука сила F, растягивающая пружину, пропорциональна ее растяжению, т. е. F=kx, где х-величина растяжения, k-коэффициент пропорциональности. Следовательно, в данном случае 1 H = k  0,01 м, откуда k=100 и F=f(x)=100x. Работу, которую необходимо затратить для растяжения пружины на 0,05 м, находим по формуле (5.6):
0,01 м, откуда k=100 и F=f(x)=100x. Работу, которую необходимо затратить для растяжения пружины на 0,05 м, находим по формуле (5.6):
|
0 ,05 |
|
0 ,05 |
|
A |
100xdx 50x2 |
|
0,125 Дж . |
|
|
0 |
|
0 |
|
|
|
|
||
|
|
|
|
4.Вычисление статических моментов и координат центра масс плоской кривой
Пусть на плоскости задана прямоугольная декартова система координат хОу.
Статическими моментами материальной точки А(х; у), в которой сосредоточе-
на масса m, относительно осей Ох и Оу называются произведения массы этой точки соответственно на ординату и абсциссу точки, т. е.
M x my, M y mx.
31

Если дана система n материальных точек A1 x1; y1 , A2 x2 ; y2 , ..., An xn ; yn , в которых сосредоточены массы m1 , m2 , ..., mn , то статическими моментами этой системы относительно осей Ox и Оу называются выражения:
n |
|
n |
|
M x |
mi yi , M y |
mi xi . |
|
i |
1 |
i 1 |
|
Центром масс такой системы материальных точек называется точка, обла- |
|||
|
|
n |
|
дающая тем свойством, что если в ней сосредоточить всю массу системы m |
mi , |
||
|
|
i |
1 |
то статический момент этой точки относительно любой оси равен статическому моменту данной системы точек относительно той же оси. Поэтому, обозначив центр масс системы через С(хс; ус), получим:
n |
|
n |
M x |
mi yi myc , M y |
mi xi mxc . |
i |
1 |
i 1 |
Таким образом, координаты центра масс системы материальных точек вычисляются по следующим формулам:
|
|
|
n |
|
|
|
|
n |
|
|
|
M y |
|
|
mi yi |
|
|
mi xi |
|
||
xC |
|
i 1 |
|
, yC |
M x i 1 |
(5.7) |
||||
|
|
|
|
|
|
|
. |
|||
m |
|
n |
|
m |
n |
|||||
|
|
|
mi |
|
m |
|
||||
|
|
|
|
|
|
|
||||
|
|
|
i |
1 |
|
|
|
i |
|
|
|
|
|
|
|
|
i 1 |
|
|||
|
|
|
|
|
|
|
|
|
||
В случае материальной плоской кривой или плоской фигуры для нахождения статических моментов и координат центра масс используется определенный интеграл.
Пусть кривая АВ длины l является графиком функции f(x), х [а; b], имеющей непрерывную производную. Будем считать, что кривая АВ однородна, т. е. линейная
плотность распределения массы постоянна. Если =1, то масса, распределенная |
|
на данной кривой, численно равна длине. Разобьем кривую на части длины li . |
|
Приняв эти части, массы которых равны mi |
li , за материальные точки, лежащие |
на расстоянии yi |
от оси Ох и расстоянии xi |
от оси Oy, получим: |
|
|
||||||||||||||||
|
|
|
|
|
|
|
M xi |
|
yi |
mi yi |
|
li , |
M yi |
|
xi mi |
xi li . |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как |
l |
1 |
f |
x |
2 |
|
x |
(см. п. 2 § 4), то |
|
|
|
|
|
|
||||||
|
i |
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
M |
xi |
|
f x 1 |
f x |
2 x , |
M |
yi |
x 1 |
f x |
2 |
x . |
|||||
|
|
|
|
|
|
|
|
i |
|
i |
|
i |
|
i |
i |
|
i |
|||
Просуммировав по всем частям разбиения кривой АВ, в пределе получим
b
M x 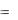
a
|
b |
|
f x 1 f x 2 dx , M y |
x 1 f x 2 dx . |
(5.8) |
a
Кроме того,
|
b |
|
m l |
1 f x 2 dx. |
(5.9) |
a
Воспользовавшись равенствами (5.7) - (5.9), запишем формулы для нахождения координат центра масс плоской кривой:
32
