3.6. Булева алгебра. Функциональная полнота

Определение. Алгеброй над множеством логических функций с двумя бинарными операциями, обозначаемыми как логическое умножение & и логическое сложение v и одной унарной операцией ( отрицанием )

• называется булевой алгеброй. Будем обозначать ее символом _B.

Рассмотрим свойства булевой алгебры.

1. Замкнутость

для  A и B  _B

A v B  _B

A & B  _B

2. Коммутативность

A & B = B & A

A v B = B v A

3. Ассоциативность

A v ( B v C) = (A v B) v C

4. Дистрибутивность

A & ( B v C) = (A & B) v (A & C)

A v ( B & C) = (A v B) & (A v C)

5. Идемпотентность

A v A = A & A = A.

6. Булева алгебра содержит элементы 0,1 , такие что для всякого

элемента A  _B справедливо:

A v 0 = A, A v 1 = 1

A & 0 = 0, A & 1 = A.

7. Для каждого элемента A  _B существует элемент , такой что

A v =1

A & =0.

8. Закон поглощения

A & (A v B) = A v A & B = A.

9. Закон Де Моргана

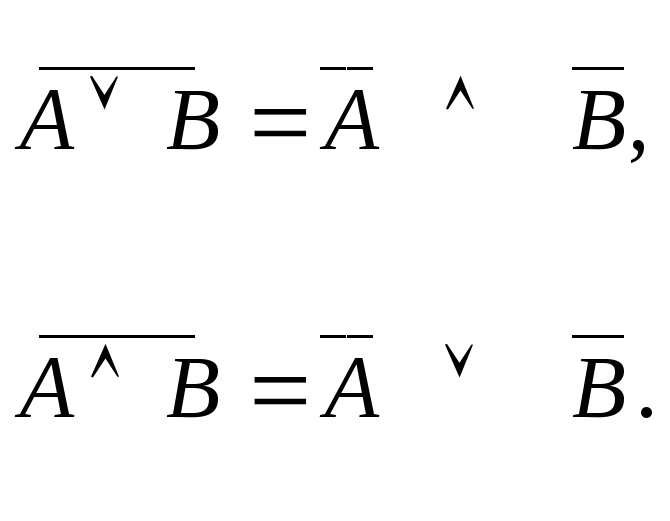
3.7. Минимизация функций алгебры логики

Введем понятие конечного автомата, как некоторой абстрактной системы, характеризующейся конечным числом состояний. Работа такого автомата напрямую связана с реализацией соответствующей ему логической функции в виде схемы или программы и поступающими из вне данными в каждый такт времени. На основе теории конечных автоматов организуется работа управляющих программ ЭВМ.

Работа конечного автомата может быть полностью описана с помощью следующей системы функций алгебры логики [7]:

y₁= f₁ (x₁ ... x_n )

y₂= f₂ (x₁ ... x_n )

...

y_m= f_m (x₁ ... x_n )

Здесь Pi = ( X1, X2, ...,Xn ); Qj = ( y1, y2, ...,ym ) - соответственно входное и выходное слово. Работа автомата может быть задана либо в виде конечных таблиц, либо в виде аналитической записи функций f_{i .}

Проблема полноты системы функций эквивалентна проблеме выбора стандартного набора элементов, из которого будет строиться автомат, при этом все функции f_i должны быть выражены через базисные функции. Уменьшение числа функций в базисе приводит к уменьшению стандартных элементов, на которых строится схема, однако, при этом увеличивается общее число элементов схемы. Возникает задача о “простейшем” представлении логических функций через систему базисных функций. Для этого используют методы минимизации:

- метод вынесения за скобки;

- метод неопределенных коэффициентов;

- метод с использованием карт Карно;

- метод Мак - Класки;

- метод Блэка.

Рассмотрим метод минимизации совершенной дизъюнктивной нормальной формы (СДНФ) с помощью карт Карно. Карта Карно - это диаграмма, состоящая из 2ⁿ квадратов, где n - число переменных. Клетка карты - одна из возможных конъюнкций, входящих в СДНФ. Минимизация на основе карт Карно осуществляется путем локализации на карте прямоугольных областей из числа клеток кратного 2.

Для работы с картой необходимо по таблице истинности составить СДНФ, затем для каждой элементарной конъюнкции проставить 1 в соответствующие клетки карты. Затем единицы объединяются таким образом, чтобы минимизировалось число логических сложений, умножений или отрицаний, что важно для экономного конструирования ЭВМ.

Рассмотрим карты Карно.

Для двух переменных: Для трех переменных:

a a

c

b

b

Для четырех переменных:

a

c

c d

d

b

Пример. Для логической функции заданной таблицей

x1	x2	x3	f
1	1	1	1
1	1	0	1
1	0	1	1
1	0	0	1
0	1	1	1

построить карту Карно и на ее основе минимизировать функцию.

Решение. Построим карту согласно описанным выше правилам.

x₁

1 1 f = x1 v x2 & x3

x_{2 1 1 1}

x₃

Рассмотрим пример представления простейшей функции картой Карно

a

c 1 1

c 1 1 d

f = b

1 1 d

1 1

b

Рассмотрим построение логической схемы для функции вида:

f1 = V2 & V4 v V3 & V1 & V2 v V3 & V4 & V1.

V1

V2

V3

V4

& & & & &

& &

&

&

1

1

f1