4. Топологическая сортировка

П

ростейшим случаем использования техники поиска в глубину на ориентированных графах является способ пометки вершины ациклического ориентированного графаG = (V, E) числами 1, 2, …, |V| так, что если из вершины i в вершину j идет ориентированное ребро, то i < j; такой способ пометки называется топологической сортировкой вершин графа G. Например, вершины графа на рис. 3.4 (б) топологически отсортированы, а на р ис. 3.4 (а) нет.

а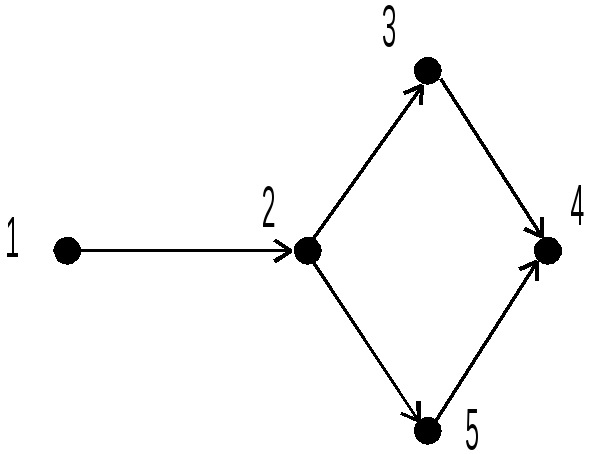) б)

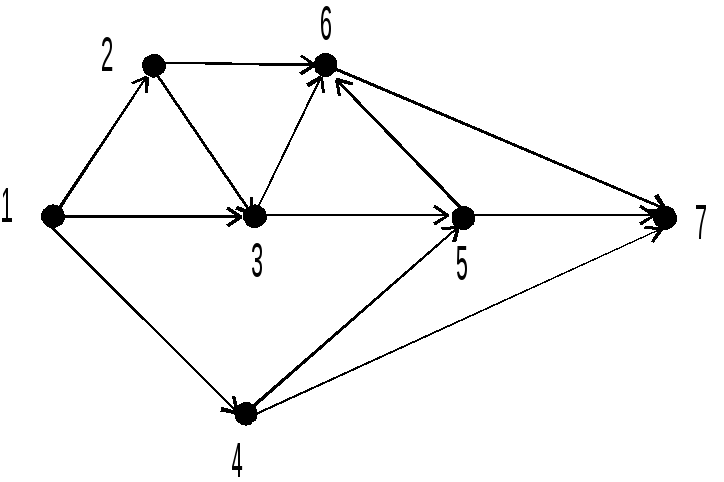
Рис. 3.4. Ациклические ориентированные графы

Топологическая сортировка может рассматриваться как процесс отыскания линейного порядка, в который может быть вложен данный частичный порядок. Граф при этом должен быть ациклическим. Топологическая сортировка полезна при анализе схем действия, где большой и сложный план представляется как ориентированный граф, вершины которого соответствуют целям плана, а ребра действиям. Топологическая сортировка дает порядок, в котором могут быть достигнуты цели.

Топологическая сортировка начинается с отыскания вершины графа G = (V, E), из которой не выходят ребра, и присвоения этой вершине наибольшего номера, а именно |V|. Эта вершина удаляется из графа вместе с входящими в нее ребрами. Поскольку оставшийся ориентированный граф также ациклический, мы повторяем процесс и присваиваем следующий наибольший номер |V| – 1 вершине, из которой не выходят ребра и т. д.

5. Транзитивное замыкание. Поиск кратчайшего пути на графе

Пусть задан граф G = (V, E), и нас интересует, какие вершины связаны между собой, не только напрямую, но и через посредство других вершин. Чтобы ответить на этот вопрос, воспользуемся матрицей смежности.

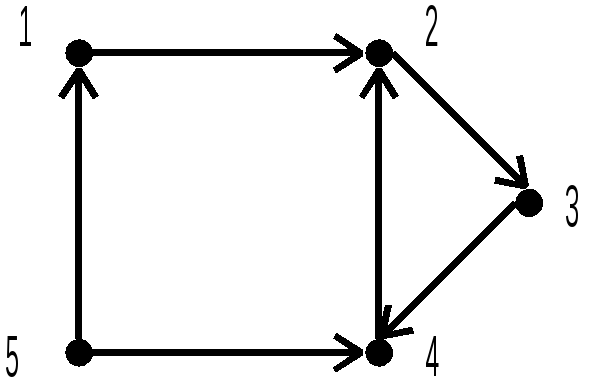
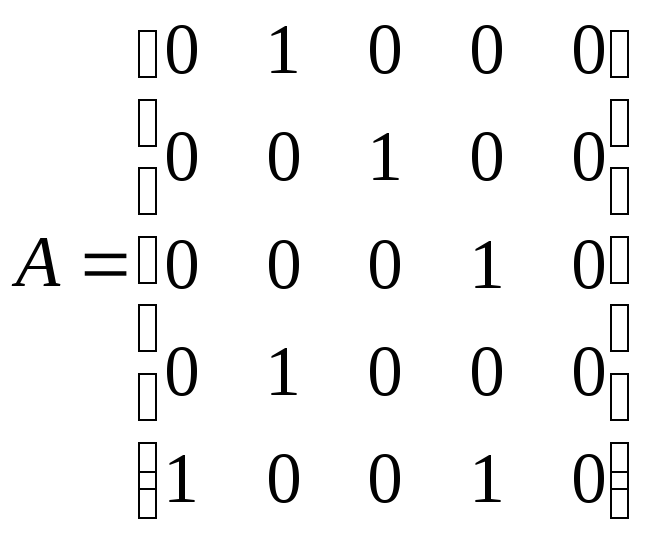
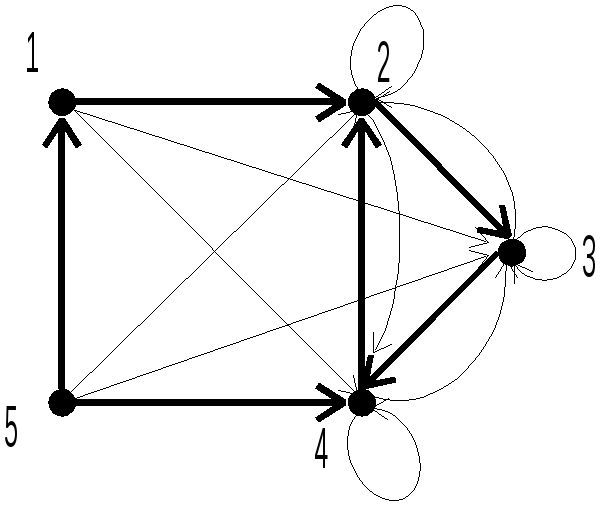
Рис. 3.5. G* — транзитивное замыкание графа G

6. Поиск кратчайшего пути

Предполагаем, что имеем простой взвешенный ориентированный граф. Несуществующие ребра будем считать ребрами с бесконечным весом. Сумму весов ребер пути будем называть весом или длиной этого пути.

Алгоритм поиска кратчайшего пути следующий.

Пусть путь ищется между вершинами s (начало) и f (конец). Мы начинаем проход из вершины s и просматриваем граф в ширину, помечая вершины значениями их расстояний от s. Процесс заканчивается, когда вершина f помечена значением ее расстояния от s и эта метка далее не меняется. Таким образом, в каждый момент времени работы алгоритма некоторые вершины будут иметь окончательные метки, а некоторые — временные.

Е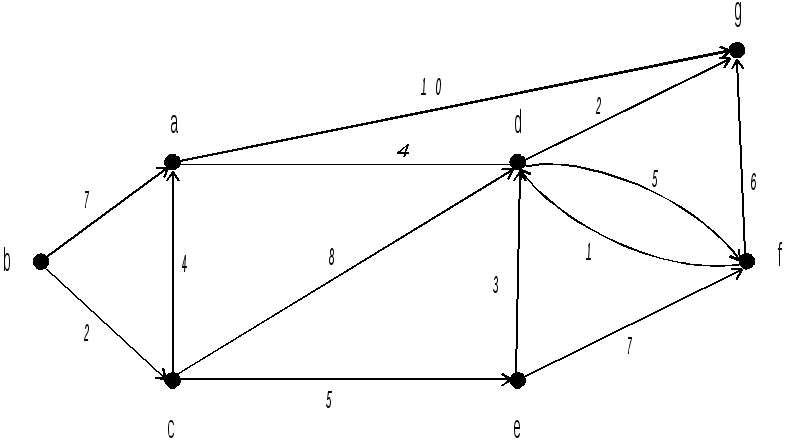сли учесть, что в начале алгоритма вершинеs присваивается окончательная метка 0 (нулевое расстояние до самой себя), а каждой из остальных вершин присваивается метка , то на каждом шаге алгоритма одной из вершин присваивается окончательная метка и поиск продолжается дальше.

Р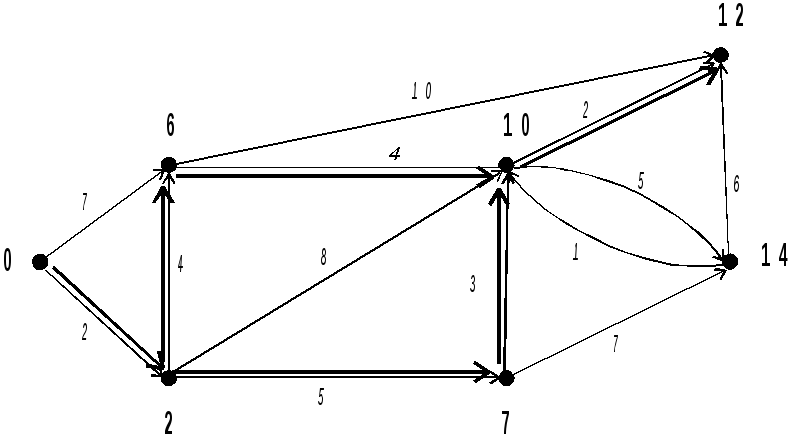ис. 3.6. Простой взвешенный граф

Как видно из нижнего рисунка граф G из b в g имеет три кратчайших пути, длины которых равны 12. Это путь b, c, e, d, g ; b, c, a, d, g и b, c, d,g.

На каждом шаге метки меняются следующим образом:

1. Каждой вершине j, не имеющей окончательной метки, присваивается новая временная метка с учетом расстояния от s до j.

2. Находится наименьшая из временных меток, она и становится окончательной меткой своей вершины. В случае равенства выбирается любая из них. Процесс продолжается до тех пор, пока вершине f не присваивается окончательная метка.