4.4. Численные распределения

При использовании случайных чисел часто требуются помимо равномерного распределения и другие виды распределений в зависимости от приложений. Например, необходимо моделировать случайное время ожидания между появлениями независимых событий, что достигается на основе применения показательного распределения случайных чисел. Иногда в случайных числах нет необходимости, но нужны случайные перестановки (случайное размещение n объектов) или случайное сочетание (случайный выбор k объектов из совокупности, содержащей n объектов).

В принципе, любая из этих случайных величин может быть получена из равномерно распределенных случайных величин U₀ , U₁ , U₂ , …, где U_i  [0, 1].

Случайный выбор из ограниченного множества

В общем случае случайные целые числа X, которые лежат между 0 и k–1, можно получить, умножив U на k и положив X = k  U (ближайшее целое снизу).

В общем случае можно получить, если необходимо, различные веса для различных целых чисел. Предположим, что значение X = x₁ должно быть получено с вероятностью p₁, X = x₂ — с вероятностью p₂, … и X = x_k — с вероятностью p_k. Для этого генерируется равномерное число U и полагается

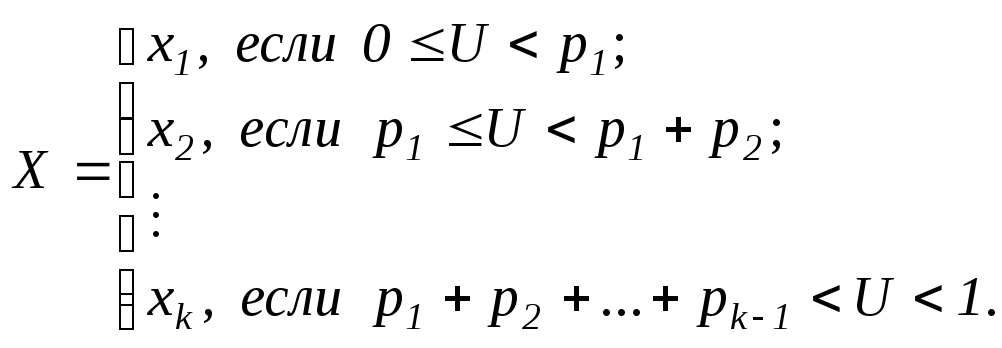
(Заметим, что .)

Общие методы для непрерывных распределений

В общем случае распределение действительных чисел может быть выражено в терминах «функции распределения» F(X), которая точно определяет вероятность того, что случайная величина X не превысит значения x:

F(X) = P_r (X  x) (4.11)

Эта функция всегда монотонно возрастает от 0 до 1, т.е. F(x₁)  F(x₂), если x₁  x₂;

F(-) = 0, F(+) = 1. Если F(X) непрерывна и строго возрастающая (так что

F(x₁) < F(x₂) , когда x₁ < x₂), то она принимает все значения между 0 и 1 и существует обратная функция F^-1(y), такая, что для 0 < y < 1 Y = F(X), тогда и только тогда, когда

X = F ^-1(y). В большинстве случаев, когда F(X) непрерывна и строго возрастающая, можно вычислить случайную величину X с распределением F(X), полагая X = F ^-1 (U), где U — равномерно распределенная случайная величина. Заметим, что если х₁ — случайная величина, имеющая функцию распределения F₁(Х), и если х₂ — независимая от х₁ случайная величина с функцией распределения F₂(Х), то max (х₁, х₂) имеет распределение F₁(Х) F₂(Х), min (х₁, х₂) имеет распределение F₁(Х) + F₂(Х) – F₁(Х)  F₂(Х).

Любой алгоритм, использующий случайные числа на входе, дает на выходе случайные величины с некоторым распределением.

Нормальное распределение

Возможно, наиболее значительным неравномерным распределением является нормальное распределение с нулевым средним значением и среднеквадратичным отклонением, равным единице:

(4.12)

Рассмотрим алгоритм вычисления двух независимых нормально распределенных случайных величин: X₁ и X₂.

Алгоритм Р. (Метод полярных координат для нормальных случайных величин).

Р1. [Получение равномерно распределенных случайных величин.] Сгенерировать две независимые случайные величины U₁ и U₂, равномерно распределенные между 0 и 1. Присвоить V₁  2U₁ – 1, V₂  2U₂ – 1. (Здесь V₁ и V₂ равномерно распределены между –1 и +1.)

Р2. [Вычисление S.] Присвоить S  V₁² + V₂².

Р3. [Проверить S  1?] Если S  1 возврат к п. Р1.

Р4. [Вычисление X₁, X₂.] Присвоить X₁ и X₂ следующие значения:

, .

Это требуемые нормально распределенные случайные величины.