2. Остовные деревья

Связанный неориентированный ациклический граф называется деревом. В связанном неориентированном графе G существует по крайней мере один путь между каждой парой вершин. Поэтому, если G — дерево, то между каждой парой вершин существует в точности один путь.

Таким образом, дерево с n вершинами содержит в точности n-1 ребер и значит деревья есть минимально связанные графы. Удаление из дерева любого ребра превращает его в несвязанный граф, разрушая единственный путь между по крайней мере одной парой вершин.

Особый интерес представляют остовные деревья графов, т.е. деревья, являющиеся подграфами графа G и содержащие все его вершины. Для построения остовного дерева (леса) неориентированного графа G, нужно последовательно просматривать ребра G, оставляя те, которые не образуют циклов с уже выбранными.

Во взвешенном графе часто бывает нужно определить остовное дерево (лес) с минимальным общим весом ребер, т.е. дерево (лес), у которого сумма весов всех его ребер минимальна. Такое дерево называется минимумом остовных деревьев. Процедура при этом такова. На каждом шаге выбирается новое ребро с наименьшим весом (наименьшее ребро), не образующее циклов с уже выбранными ребрами; этот процесс продолжается до тех пор, пока не будет выбрано |v|–1 ребер, образующих остовное дерево Т, где v — число узлов дерева. Этот процесс известен как жадный алгоритм.

Другой способ получения минимума остовных деревьев, который не требует ни сортировки ребер, ни проверки на цикличность на каждом шаге, известен как алгоритм ближайшего соседа.

Прохождение графа начинается с некоторой произвольной вершины а в заданном графе. Пусть (a, b) — ребро с наименьшим весом, инцидентное a; ребро (a, b) включается в дерево. Затем среди всех ребер, инцидентных либо а, либо b, выбирается ребро с наименьшим весом, и оно включается в частично построенное дерево. В результате в дерево добавляется новая вершина, например c. Повторяя процесс, ищем наименьшее ребро, соединяющее a, b или c с некоторой другой вершиной графа. Процесс продолжается до тех пор, пока все вершины из G не будут включены в дерево, т.е. пока дерево не станет остовным.

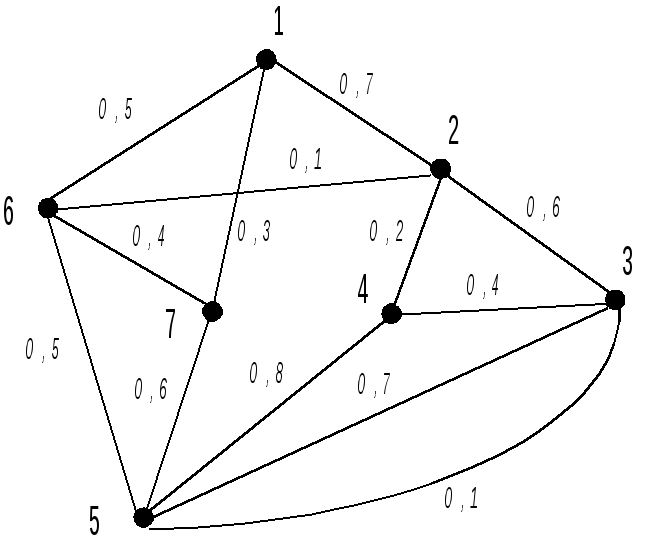
Примеры. В основе — граф рис. 3.1.

1. Жадный алгоритм

6 — начало:

 = 1,7

2. Алгоритм ближайшего соседа

 = 1,7

Рис. 3.2. Алгоритмы на графах

Остовные деревья необходимы для расщепления графов с целью исключения циклов. Они используются при организации работы коммутаторов коммуникационных сетей.

3. Поиск по графу в глубину. Топологическая сортировка

Один из способов исследования всех вершин и ребер графа основан на процедуре прохождения графа методом поиска с возвращением, т.е. на исследовании графа в глубину. Рассмотрим это на примере неориентированного графа. Когда мы посещаем вершину vV, мы идем по одному из ребер (v, w), инцидентному v. Если вершина w уже пройдена (посещалась ранее), мы возвращаемся в v и выбираем другое ребро. Если вершина w еще не пройдена, то заходим в нее и применяем процесс рекурсивно к w. Если все ребра, инцидентные вершине v, уже просмотрены, мы идем назад к ребру (u, v), по которому пришли в v, и продолжаем исследование ребер, инцидентных u. Процесс заканчивается, когда все вершины пройдены и когда мы пытаемся вернуться назад из вершины, с которой началось исследование.

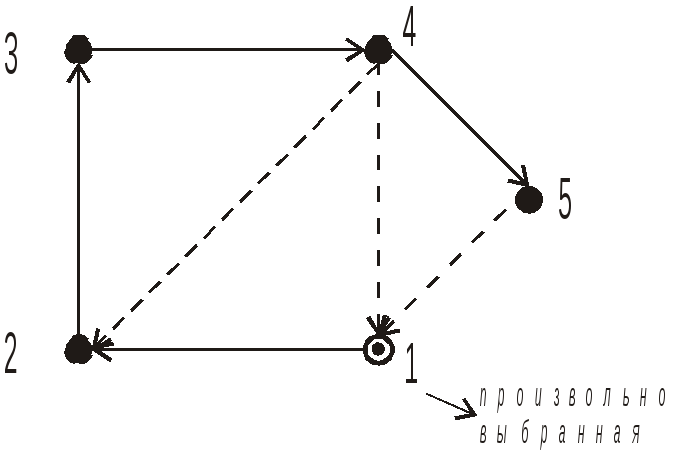
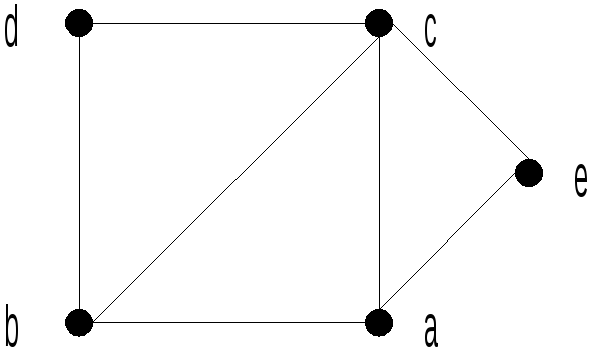
a: b, c, e

b: a, c, d

c: a, b, d, e

d: b, c

e: a, c

Рис. 3.3. Граф G. Структура смежности G. Пройденный граф

Как видно на рис. 3.3 поиск в глубину превращает исходный неориентированный граф G в ориентированный граф , индуцируя на каждом ребре направление прохождения. Сплошные линии образуют ориентированное остовное дерево.

Ориентированное остовное дерево, получаемое в результате поиска в глубину на простом связанном неориентированном графе, называется DFS-деревом. Ребра называютсяобратными, т.к. ведут от потомка к предку.

Для реализации процедуры поиска в глубину нам необходимо отличать уже пройденные вершины от еще не пройденных. Этого можно достигнуть путем постепенной нумерации вершин числами по мере того, как мы в них попадаем.