Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4605 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Санкт-Петербургский государственный архитектурно-строительный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Денисихина

.pdf
Скачиваний:
67
Добавлен:
29.03.2015
Размер:
18.11 Mб
Скачать
☆

1-66

Министерство образования и науки Российской Федерации

Санкт-Петербургский государственный архитектурно-строительный университет

Д.М. ДЕНИСИХИНА

ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ STAR-CCM+

ПРИ ПРОЕКТИРОВАНИИ СИСТЕМ ВЕНТИЛЯЦИИ

Учебное пособие

Санкт-Петербург

2013

УДК 697.95

Рецензенты: Бурцев Сергей Иванович, д.т.н., профессор, управляющий партнер ГК «БЮРО ТЕХНИКИ» Дацюк Тамара Александровна, д.т.н., профессор, декан факультета ИЭС СПбГАСУ

Денисихина, Д. М.

Использование программы STAR-CCM+ при проектировании систем вентиляции: учеб. пособие / Д. М. Денисихина; СПбГАСУ. –

СПб., 2013. – с.

Цель данного учебного пособия– познакомить студентов с современными методами расчета в области вентиляции и кондиционирования, использование которых на стадии проектирования позволяет получать энергоэффективные решения. В пособии рассмотрены теоретические основы математического моделирования турбулентных течений и получения дискретных аналогов дифференциальных уравнений. На конкретном примере показаны все этапы работы с программным обеспечением STAR-CCM+, позволяющим выполнять численные расчеты для решения практических задач вентиляции.

Предназначено для студентов специальности 270109 «Теплогазоснабжение и вентиляция» всех форм обучения.

Ил. 69. Библиогр.: 8 назв.

Рекомендовано Редакционно-издательским советом СПбГАСУ в качестве учебного пособия.

©Д. М, Денисихина, 2013

©Санкт-Петербургский государственный архитектурно-строительный университет, 2013

2

ВВЕДЕНИЕ

Энергоэффективность это не только энергосбережение, направленное на уменьшение энергопотребления объектом, но и полезное (эффективное) расходование этой энергии. Так, применительно к системам вентиляции и кондиционирования воздуха (ВиКВ), можно уменьшать потребляемую ими электроэнергию, но если запроектированные системы на практике не смогут обеспечить комфортные условия для человека и/или технологические требования к объекту, следовательно, энергия, ресурсы расходуются не эффективно. Таким образом, если бороться за энергоэффекттивность инженерных систем зданий, то необходимо в первую очередь повысить уровень выполняемых проектных работ.

Успешность конкретного проекта по системам ВиКВ в конечном счете будет определяться выбранной схемой воздухораспределения. Так, неправильное представление о характере распространения приточных струй, их взаимного влияния, взаимодействия с источниками тепло и влаговыделений и т. д. приведет к тому, что неверно будут определены параметры воздуха на притоке (скорости, температура, влажность), вид приточных устройств (сопла, решетки, диффузоры), мощность систем кондиционирования. То есть при последующей эксплуатации запроектированные системы не обеспечат требуемые параметры в объеме помещения.

Методы расчета воздухораспределения, прочно вошедшие в проектную практику уже более 70 лет, базируются на закономерностях струйных течений и их применимость ограниченна определенным набором несложных течений с существенным преобладанием либо вынужденной, либо свободной конвекции. Данные подходы не позволяют предсказать параметры воздушной среды в объеме со смешанно-конвективными течениями, неравномерным распределением источников тепло-, влаговыделений, сложным взаимодействием приточных струй т. д. А именно к таким объектам относятся современные театры, бассейны, стадионы, бизнес-центры, атриумы, торго- во-развлекательные комплексы и т. д.

Использование методов численного решения исходной системы дифференциальных трехмерных уравнений Навье-Стокса позволяет отыскать решение (распределение температуры, подвижности, влаж-

3

ности, концентрации СО2 по объему помещения) вне зависимости от сложности геометрии, особенностей взаимодействии приточных струй и т. д., в том числе и для сложных смешанно-конвективных течений.

Появление универсальных вычислительных программ (STARCCM+, STAR-CD, FLUENT, CFX и др.) избавило от необходимости писать собственные коды, которые неизбежно были бы ограничены, как по возможности описания сложных геометрий, так и по набору физических моделей и тому подобное.

Внастоящее учебном пособии подробно изложены и на конкретном примере показаны шаги работы с помощью современного гидродинамического пакета STAR-CCM+. В отличие от известного гидродинамического комплекса STAR-CD, данный пакет оснащен встроенным построителем геометрии и удобным интерфейсом для построения расчетных сеток, что способствует более успешному и быстрому освоению пакета STAR-CCM+.

Вто же время для многих исследовательских работ, требующих наличия широкого набора физических моделей, рекомендуется пользоваться пакетом STAR-CD.

Часть 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

1.1. Основные уравнения

С точки зрения физики потоков все вентиляционные течения можно разделить на три класса в зависимости от соотношения сил тяжести и инерции в потоке жидкости, т. е. в зависимости от значения числа Ричардсона течения:

R =

Gr

=

gLβ T

.

 

 

i

Re

2

 

u 2

 

 

Так, если Ri<<1, то в течении преобладает вынужденная конвекция. К таким задачам относятся течения в каналах, воздуховодах, вентиляция изотермичными струями и т. д.

4

Если Ri>>1, то течение обусловлено в основном естественноконвектививными потоками, например восходящий поток над нагретым источником, вытесняющая вентиляция.

Наиболее сложными для описания являются смешанно– конвективные течения (т. е. течений с одновременным действием свободно-конвективных и вынужденных сил). Для таких течений число Ri≈1. Это имеет место для большого числа вентиляционных течений, где сосредоточенная подача воздуха соседствует со свободноконвективными струями, поднимающимися от человека, оборудования и т. д. А также, например, при совместном использовании вытесняющей и перемешивающей вентиляции, что характерно для таких объектов как театры, стадионы и т. д.

Развитие вычислительных методов, вычислительных ресурсов (кластеров, суперкомпьютеров) позволило находить частные решения для любого класса вентиляционных течений, в том числе и теоретически плохо изученных смешанных течений.

Поведение существенно неизотермичных течений описывается системой дифференциальных уравнений относительно осредненных [1] параметров потока:

уравнение сохранения массы

 

 

 

 

 

 

 

 

 

 

 

 

 

R

= 0,

 

 

 

 

 

 

 

 

 

 

 

(1)

 

 

 

 

 

∂ρ + Ñ × (ρV )

 

 

 

 

 

 

 

 

 

 

 

уравнение сохранение импульса

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ρV

 

 

R R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t + Ñ × (ρVV ) = -Ñp + Ñ × (τ + τt ) + ρg,

(2)

где t – время, V – вектор скорости, p –

пьезометрическое давление, ρ –

плотность.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тензор вязких напряжений τ, определен с помощью реологиче-

ского закона Ньютона

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

R

 

2

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

τ = μ(ÑV + [ÑV ]T ) -

μÑ × VI,

(3)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а тензор турбулентных напряжений

 

t

– в соответствии с обобщенной

τ

гипотезой Буссинеска

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

R

 

 

2

 

R

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

τt = μt (ÑV +

[ÑV ]T

) -

μt

Ñ × VI -

ρk I ,

(4)

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

3

 

 

 

 

 

 

уравнение состоянияρ = p0 ,

RT

5

уравнение сохранения энергии

∂ρE

R

 

 

R

 

 

 

 

R

R

, (5)

 

 

 

 

 

 

t

+ Ñ × (V [ρE + p]) = Ñ × (V

×[τ + τt ]) - Ñ × (q

+ qt ) + Sr

 

 

 

 

 

 

 

 

 

 

 

молекулярная составляющая вектора плотности теплового потока

 

q = -λÑT ,

 

(6)

турбулентная составляющая вектора плотности теплового потока

 

 

R

= -λtÑT ,

 

(7)

 

qt

 

турбулентная теплопроводность определяется как

 

 

 

λt

=

c pμt

.

 

 

 

 

 

 

(8)

 

 

 

 

 

 

 

 

 

 

 

Prt

 

 

 

 

 

 

 

Для получения информации о полях концентрации вредных веществ, пара система дополняется уравнением сохранения массы для компоненты газа:

 

R

R

 

R

 

),

(9)

∂ρci + Ñ × (ρc V ) = -Ñ × (J

 

+ J

 

t

i

 

j

 

jt

 

 

 

 

 

 

 

диффузионный поток компоненты

J j = -ρDÑci ,

(10)

турбулентный поток массы компоненты

R

 

= -

μt

Ñc .

(11)

J

jt

 

 

 

 

i

 

 

 

 

Sct

 

При расчете смеси в уравнении переноса энергии (5) молекулярную и турбулентную составляющие вектора плотности теплового потока следует рассчитывать с учетом переноса тепла компонентой:

молекулярная составляющая вектора плотности теплового потока

R

= -λÑT + ∑ h j J j ,

(12)

q

j

турбулентная составляющая вектора плотности теплового потока

R

= -λt ÑT + ∑ h j J jt ,

(13)

qt

j

а в уравнениях сохранения плотность следует трактовать как плотность смеси (например воздух +водяной пар).

Для нахождения характеристик турбулентности необходимо использование той или иной модели турбулентности, например k-ε:

 

R

 

μ

t

 

 

 

(ρk) +Ñ× ρVk -(μ+

 

 

)Ñk

= μt (P + PB ) -ρε,

(14)

t

 

σk

 

 

 

 

 

 

 

 

 

6

 

 

 

 

R

 

 

 

 

μt

 

 

 

 

 

ε

 

(ρε) + Ñ × ρVε - (μ +

)Ñε

= Cε1

μt P +

 

t

 

 

 

 

 

 

 

 

σε

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

ε2

 

(15)

 

 

+ C

 

ε

μ

P - C

 

ρ

,

 

 

 

 

ε3 k

ε2

 

 

 

 

 

 

t

 

B

 

 

k

 

 

генерационный член в уравнениях переноса (12) и (13)

 

 

P = μ(ÑV + [ÑV ]T ) ××ÑV ,

(16)

PB – дополнительный генерационный член, учитывающий влияние сил плавучести на характеристики турбулентности

 

= -

1

 

1 R

×Ñρ.

(17)

PB

 

 

 

g

Sct

 

ρ

 

 

 

 

 

 

Приведенная формулировка k-e модели является высокорейнольдсовой. Поэтому для постановки граничный условий на стенке должны использоваться так называемые стеночные функции, базирующиеся на предположении, что профиль скорости в пристенном турбулентном пограничном слое имеет линейный и логарифмический участки:

uP+ = uP uτ

y+ , y+ ≤ y+ = m

1 ln(Ey+ ), y+ > ym+ .

κ

Значение диссипации кинетической энергии турбулентности ε в пристенной ячейке определяется из условия локального равновесия (равенство генерации и диссипации турбулентности)в пристенной ячейки:

 

C

3

4 k

3

 

 

μ

2

 

εP =

 

 

P

.

 

 

 

 

 

 

κyP

Что касается уравнения для переноса k, то оно решается вплоть до стенки с использованием граничного условия

∂k = 0.

n

Для помещений, в которых присутствуют существенные теплопритоки от освещения, массива зрителей, оборудования пренебрежение раздельного учета лучистой составляющей тепловых потоков может привести к искажению прогнозируемого поля температуры, циркуляции воздуха в помещении, картины течения во всем объеме.

7

В связи с этим для расчета такого типа течений систему уравнений (1)-(17) необходимо дополнить уравнениями радиационного теплообмена [2]:

R R R

R R

σT 4

 

σ

s

4π

R R

R R

Ñ × (I (r , s )s ) + (a + σs )I (r , s ) = a

 

+

 

 

I (r , s¢)F(s × s¢)dW¢, (18)

π

4π ∫

 

 

 

 

 

 

 

 

 

 

0

 

R

где r – радиус-вектор, s – вектор направления излучения, s′ – вектор

рассеяния, a –

коэффициент поглощения,

σs

– коэффициент рассея-

ния, I – полная интенсивность

излучения,

зависящая от радиус-

вектора и направления излучения, Φ –

фазовая функция, определяю-

щая диаграмму рассеяния, Ω′ – телесный угол, σ – постоянная Стефа-

на -Больцмана 5,67×10-8 W/(m2×K4).

1.2 Методы получения дискретного аналога

Для решения уравнений Рейнольдса используют численные методы [3, 4, 5, 6, 7], выбор которых зависит от решаемой задачи.

Смысл численного решения дифференциального уравнения состоит в том, чтобы получить значения искомой переменной в рассматриваемом пространстве. В численном методе рассматриваются значения переменных в конечном числе точек расчетной области. Метод дискретизации сводится к получению системы алгебраических уравнений, которые являются дискретными аналогами исходных дифференциальных уравнений. При этом предполагается, что при достаточно мелкой сетке, решение дискретных уравнений является хорошим приближением к точному решению исходных дифференциальных уравнений. Дискретизация дифференциальных уравнений может быть выполнена разными методами, при этом используемая схема должна быть устойчивой и сходящейся.

Вобщем случае процедура решения задачи сводится к следующим этапам:

1. Выполняется дискретизация дифференциальных уравнений, т. е. переход к алгебраическим уравнениям относительно искомых переменных (скорости, давления, температуры и т. п.) в конечном числе точек в пределах расчетной области.

2. Производится решение алгебраических уравнений.

Внастоящее время наиболее распространены следующие методы решения уравнений Рейнольдса:

8

∙конечных разностей;

∙контрольного объема:

∙конечных элементов.

В последнее время приоритет отдается методу контрольного объема, который подробно рассмотрен в работе [4].

1.2.1. Метод конечных разностей

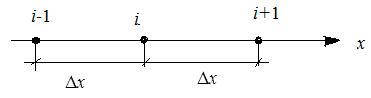
Одним из общеизвестных и наиболее простых методов получения конечно-разностных уравнений является разложение искомой функции в ряд Тейлора в окрестности точки xi (рис. 1):

f (xi

где xi = xi+1 − xi .

+ x ) = f (x ) + ∂f

 

 

x +

1

 

 

∂2 f

 

 

 

 

 

 

i

i

∂x

 

 

i

2!

∂x2

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

+

1

∂3 f

 

 

x3

+ ... +

1

∂n f

 

xn

 

 

 

 

 

3! ∂x3

 

i

i

 

 

 

n! ∂xn

 

i i

 

 

 

 

 

 

xi2 +

i(19)

+...,

Рис. 1. Схема, поясняющая получение дискретного аналога

Данный ряд может быть оборван после любого числа членов, причем возникающая в результате ошибка (ошибка аппроксимации) определяется в основном следующим членом разложения, т. е. вели-

чиной x (расстоянием между соседними ячейками), например

f (x +

x ) = f (x ) + ∂f

 

 

x +

1

∂2 f

x2

+ O(

x3 ),

(20)

 

 

 

 

 

i

i

i

∂x

 

 

i

2

∂x2

i

 

i

 

 

 

 

 

i

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где O( xi3 ) – остаточный член, указывает на то,

что точность аппрок-

симации соответствует точности 3-го порядка.

Ошибка аппроксимации будет быстро уменьшаться с уменьшением x i . Дискретизация производных может быть выполнена с раз-

ным порядком точности.

Если отбросить третий член ряда, то

9

f (x + x ) = f (x ) +

∂f

 

 

 

x + O( x2 ),

 

∂x

 

 

i

i

i

 

i

i

i

 

откуда после перегруппировки слагаемых получим дискретный аналог первой производной первого порядка точности

∂f

 

 

=

f (xi + xi ) − f (xi )

+ O( x ),

 

∂x

 

 

 

 

 

 

 

 

i

 

 

 

 

x

i

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

или

 

∂f

 

 

 

fi +1 − fi

 

 

 

 

 

 

 

 

 

=

..

(21)

 

 

 

 

 

 

 

 

 

∂x

 

i

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

Центрально-разностная аппроксимация в точке xi получается как разность разложений функции в ряд Тейлора в точках xi +1 и xi –1 относительно рассматриваемой точки xi,

∂f

 

 

=

fi +1 − fi −1

+ O(

x2 ),

(22)

 

∂x

 

 

 

 

i

 

2 x

i

 

 

 

 

 

 

 

i

 

 

которая имеет второй порядок точности.

Аналогично, центрально-разностная аппроксимация второй производной со вторым порядком точности может быть получена, если оставить первые три члена разложения ряда Тейлора,

 

 

 

 

 

∂f

 

 

 

 

∂2 f

 

 

x2

 

 

 

 

 

 

 

 

 

 

 

 

 

f (x +

x ) =

f (x ) +

∂x

 

 

x

+

∂x2

 

 

i

+ O(

x

3 ). (23)

 

 

 

 

 

i

i

 

 

i

 

i

i

 

 

i

2

 

i

 

 

 

 

Осуществляя перегруппировку, окончательно находим:

 

 

 

∂2 f

 

=

fi +1 − 2 fi

+ fi −1

+ O(

x2 ).

 

(24)

 

 

 

 

∂x2

i

 

 

 

 

 

 

x2

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

Отметим, что при подстановке в уравнения сохранения (1)–(18) дискретных аналогов производных ошибкаO( xik ) , также попадает в

уравнение, где k – точность порядка аппроксимации.

Данный метод получения дискретных аналогов производных достаточно прост. Однако при его применении к уравнениям (1)–(18) может нарушиться принцип консервативности, который заключается в том, что законы сохранения должны выполняться не только в целом для всей расчетной области, но и для любого внутреннего объема. В этом случае для получения правильного решения могут потребоваться слишком мелкие сетки, что при решении инженерных задач может оказаться достаточно сложным.

1.2.2 Метод контрольного объема

10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности