Методические указания по выполнению лабораторной работы
Методы численного интегрирования
(Методические указания по выполнению лабораторной работы)
Целью лабораторной работы является изучение методов вычисления значений определённых интегралов [1] вида
b |
|
J = ∫ f ( x )dx , |
( 1 ) |
a
здесь a и b - нижний и верхний пределы интегрирования, функция f(x) непрерывная на отрезке [a, b].
При выполнении работы необходимо вычислить значение одного или нескольких определенных интегралов, используя для этого методы, относящиеся к классу методов Ньютона - Котеса.
Методы этого класса основаны на полиномиальной аппроксимации подынтегральных функций.
В работе рассматриваются три варианта аппроксимации подынтегральной функции:
-прямоугольниками,
-трапециями и
-параболической функцией (метод Симпсона)(1).
Методы численного интегрирования применяются в случаях, когда нахождение первообразной функции невозможно или очень сложно. В теоретическом курсе высшей математики интеграл определяется как предел
b |
|
|
∑n |
f ( ξ i ) x i + R |
|
∫ f ( x ) dx |
= |
lim |
( 2 ) |
||
a |
|
max x i |
→ 0 i =1 |
|
|
где ξi [xi-1 , xi], а R - погрешность вычисления интеграла.
Эта формула определяет сущность всех методов численного интегрирования. Интервал интегрирования [a; b] разбивается на n равных отрезков h=(b-a)/n. Название метода соответствует способу выбора аппроксимирующей функции.
Так выбор в пределах интервалов [xi;xi+1] одной точки ξi для вычисления в ней значения интегрируемой функции f(ξi) определяет аппроксимацию полиномом нулевой степени - константой. Такой выбор точки ξi неоднозначен.
1 В методе Симпсона подынтегральная функция заменяется (аппроксимируется) параболой.
1 |
Любимов Е.Б. |
|
Методические указания по выполнению лабораторной работы
Значение интеграла на интервале [xi; xi+1] заменяется площадью прямоугольника, равной f(ξi)h.
Так, при выборе точек ξi = xi (i=0, 1, 2,..., n-1), определяющих левые границы подинтервалов, метод называется методом левых прямоугольников.
Если ξi = xi+1 (i=0, 1, 2, ... , n-1), (точки, определяющие правые границы подинтервалов) метод называется методом правых прямоугольников, а если ξi =(xi+xi+1)/2 (i=0, 1, 2,..., n-1) – метод средних прямоугольников.
Методы левых и правых прямоугольников имеют сравнительно невысокую точность. Погрешность этих методов больше, чем погрешность метода средних прямоугольников. Погрешность метода средних прямоугольников сравнима с погрешностью метода трапеций или с погрешностью метода Симпсона.
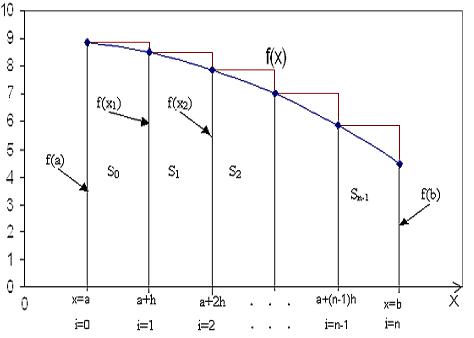
На рис. 1 показана схема замены интегрируемой функции, определяющей площадь S криволинейной трапеции, ограничиваемую осью абсцисс Oх, криволинейным участком, определяемым функцией f(x) и прямыми x=a, x=b, множеством левых прямоугольников.
Рис.1. Графическое представление интегрирования методом левых прямоугольников
Для вычисления площади криволинейной трапеции отрезок [a, b] делится на n равных частей. Точки деления перенумеруем от 0 до n, так чтобы первая точка имела номер 0: х0 = а, а последняяномер n: хn = b. Расстояние между соседними точками h = xi+1 - xi можно вычислить по формуле
2 |
Любимов Е.Б. |
|
Методические указания по выполнению лабораторной работы
h = |
b −a |
. |
( 3 ) |
|
|||
|
n |
|
|
Значения xi определяются по формуле
xi =a+i*h (i= 0, 1,..., n).
Площадь криволинейной трапеции S можно определить как сумму площадей элементарных фигур Si :
b |
|
|
+ R |
( 4 ) |
∫ f ( x )dx = S + R = n∑−1S |
i |
|||
a |
i =0 |
|
|
|
Слагаемое R обозначает погрешность формулы, используемой для вычисления значения интеграла.
Таким образом, значение интеграла определяется как сумма площадей Si . Элементарные криволинейные трапеции в методах численного интегрирования моделируются элементами с легко вычисляемыми площадями. Такими как прямоугольники, трапеции и фигуры, ограничиваемые с одной стороны параболой.
Методы прямоугольников
Метод прямоугольников чаще всего реализуется в трёх вариантах: левых прямоугольников, правых прямоугольников и средних прямоугольников.
В формулах метода прямоугольников одна сторона каждого прямоугольника h определяется по формуле (3), а значение второй стороны в зависимости от метода равно f(xi) для i=0, 1, 2,...,n-1 в формуле левых прямоугольников:
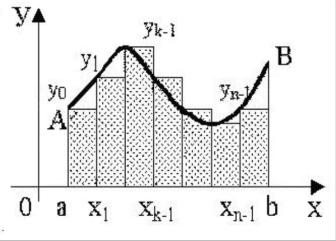
Рис. 2. Метод левых прямоугольников ξ= x (i = 0, 1, 2, … , n-1)
b |
|
i i |
|
= h n∑−1 f ( a + i h ) + RЛП ( 5 ) |
|
∫ f ( x )dx = n∑−1 f ( xi ) h + RЛП |
||
a |
i =0 |
i =0 |
3 |
Любимов Е.Б. |
|
Методические указания по выполнению лабораторной работы
f(xi) для i= 1, 2,...,n в формуле правых прямоугольников:
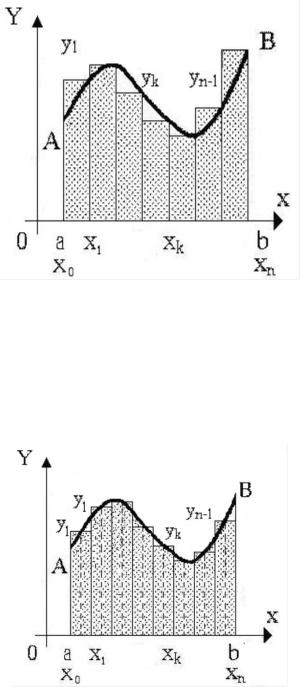
Рис. 3. Метод правых прямоугольников: ξi = xi (i = 1, 2, … , n).
b |
|
n |
+ R ПрП |
n |
+ i h ) + R ПрП ( 6 ) |
∫ f ( x )dx |
= |
∑ f ( xi ) h |
= h ∑ f ( a |
||
a |
|
i =1 |
|
i =1 |
|
и f([xi + |
|
xi+1] / 2) для |
i=0, |
1, 2,...,n-1 в |
формуле средних |
прямоугольников:
Рис. 4. Метод средних прямоугольников: ξi =( xi +xi+1)/2 (i = 0, 1, 2, … , n-1)
∫ f ( x )dx = n∑−1 f ( xi + xi+1 |
) h |
( 7 ) |
||
b |
|
|
|
|
a |
i=0 |
2 |
|
|
Обратите внимание на индексы в определении значения аргумента xi в обращениях к функциям, используемых для вычисления площадей элементарных прямоугольников и на то, что во всех вариантах метода суммируются площади (n-1) - го прямоугольника.
4 |
Любимов Е.Б. |
|