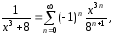Решение задачи № 3

В этой задаче рассматривается степенной ряд, т.е. бесконечный ряд вида

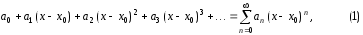
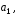
где 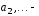фиксированные числа, а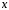пробегает некоторый интервал. Точнее, ряд (1) называетсястепенным рядом с центром 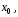или рядом по степеням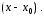

Центр сходимости степенного ряда задачи 3 находится в точке 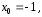так как

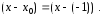
Исследование сходимости степенного ряда основано на использовании следующей теоремы, которая является следствием теоремы Абеля.

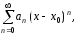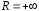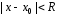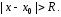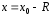Теорема. Пусть дан степенной ряд тогда существует такое число (которое может также принимать значение), что ряд абсолютно сходится прии расходится приПрии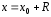ряд может либо сходиться, либо расходиться.

Число 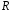называетсярадиусом сходимости рассматриваемого ряда, а интервал 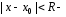егоинтервалом сходимости (в предположении, конечно, что ). Интервал сходимости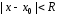можно представить в виде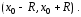

Если закрепить конкретное значение 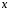, то степенной ряд (1) превращается в бесконечныйчисловой ряд, который может либо сходиться, либо расходиться.

Для определения интервала сходимости степенного ряда воспользуемся признаком Даламбера, применив его к ряду из абсолютных величин членов исходного ряда

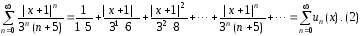
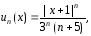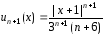Так как тои

Напоминаем, что мы закрепили конкретное значение .

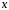Найдем предел

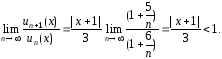
В соответствии с признаком Даламбера (см. решение задачи 1) ряд (2) сходится, а исходный ряд сходится абсолютно, если значения переменной 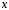удовлетворяют неравенству

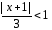или

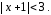
Отсюда видно, что радиус сходимости степенного ряда 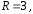центрмы определили ранее.

Интервал сходимости степенного ряда представим в следующем виде

или

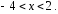
Остается определить поведение степенного ряда на концах интервала сходимост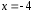и и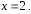

При 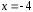получаем знакочередующийся числовой ряд

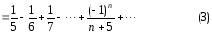
При 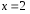получаем числовой ряд с положительными членами

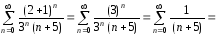
Начинать исследование на сходимость нужно с ряда (4), так как он составлен из абсолютных величин членов ряда (3). Если ряд (4) сходится, то решение на этом практически заканчивается.

Заметим, что не следует повторно применять признак Даламбера при исследовании на сходимость ряда (4), так как концевые точк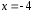и и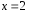интервала сходимости являются решением уравнения

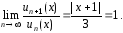
В этом случае признак Даламбера не работает.

Применим к исследованию ряда (4) интегральный признак Коши (см. решение задачи 2).

Тогда 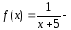непрерывная положительная убывающая функция, определенная при

Поскольку интеграл

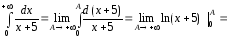
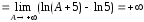
расходится, то расходится и ряд (4).

Следовательно, ряд (3) не имеет абсолютной сходимости. Исследуем его на условную сходимость с помощью признака Лейбница.

Так как

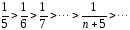и

то условия признака Лейбница выполнены, и значит, знакочередующийся ряд (3) сходится условно (или неабсолютно).

Ответ. Степенной ряд сходится абсолютно на интервале 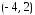, при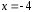 ряд сходится условно (или неабсолютно), на интервалах 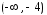и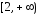ряд расходится.

Решение задачи № 4

В этой задаче требуется разложить данную функцию в степенной ряд и указать интервал, на котором это разложение справедливо.

Напомним, что если функция 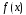в некоторой окрестности точки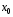имеет производные любого порядка, то для нее можно построить степенной ряд

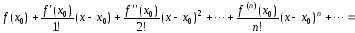
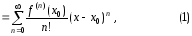
который называется рядом Тейлора в точке .

В формуле (1) использованы следующие обозначения:

• производная нулевого порядка совпадает с самой функцией;

• функция 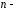факториал определяется следующим образом:

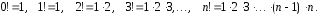
Частичные суммы ряда Тейлора называют многочленами Тейлора функция в точке.

При 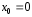ряд Тейлора называют рядом Маклорена.

Функция , определенная в некоторой окрестности точки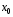, называетсяаналитической в точке , если ее можно представить в виде суммы сходящегося степенного ряда с центром

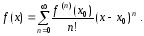
В этом случае говорят, что функция 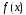разлагается в ряд Тейлора по степеням

Функция 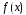, определенная вблизи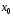и имеющая производные всех порядков, не обязана быть аналитической в этой точке. Может случиться, что ее ряд Тейлора имеет нулевой радиус сходимости или ненулевой радиус сходимости, но сумма его не равна.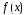

При разложении в ряд многих элементарных функций можно использовать известные разложения функций в ряд Маклорена:

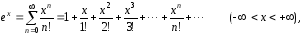
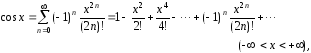
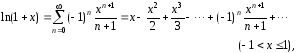
Для того, чтобы разложить функцию 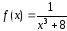в ряд по степеняммы воспользуемсябиномиальным разложением (результат принадлежит Ньютону)

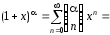
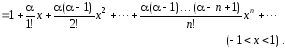
Здесь 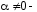любое действительное число и биномиальные коэффициенты определяются следующими формулами

Так как наша функция может быть представлена в виде

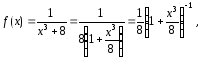
то мы воспользуемся биномиальным разложением с показателем 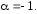Вычислим биномиальные коэффициенты при этом значении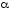

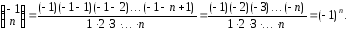
В результате получим разложение

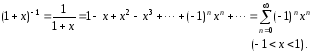
Заменяя здесь на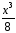, получим требуемое разложение функции

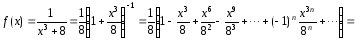
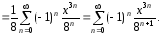
Это разложение справедливо, когда

или

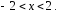
Ответ.