- •Геометрические характеристики плоских сечений.
- •Центробежный момент инерции
- •Изменение моментов инерции при параллельном переносе осей координат.
- •Условие жесткости
- •) Это 23 задача. Тут сам метод помимо формулы – прочтите лишним не будет. Метод Максвелла – Мора определения перемещений
- •Основные определения
- •Метод сил
Условие жесткости
Условие жесткости стержня
O`(погонный угол закр.)=Mкрmax/G*Jро<[O]
Критерии пластичности и разрушения. Первая, вторая, третья и четвертая теории прочности. Тория Мора. Общие сведения о различных гипотезах прочности и пластичности. Общий план решения задачи о проверки прочности.
В общем случае опасное напряженное состояние элемента конструкции зависит от соотношения между тремя главными напряжениями (s1,s2,s3). Т.е., строго говоря, для каждого соотношения нужно экспериментально определять величину предельного напряжения, что нереально. Поэтому были приняты такие методы расчета прочности, которые позволяли бы оценить степень опасности любого напряженного состояния по напряжению растяжения — сжатия. Они называются теориями прочности (теории предельных напряженных состояний).
1-ая теория прочности (теория максимальных нормальных напряжений)Установил Кулон: При любом напр. состоянии хрупкое разрушение будет, если макс. норм. напряжение достигает предельного значения для данногоматериала Главный недостаток: не учитываются два других главных напряжения. Подтверждается опытом только при растяжении весьма хрупких материалов (стекло, гипс). В настоящее время практически не применяется.
Условия разрушения:
сигма max<сигма пред.(экспиремент на растяжение)
сигма экв.=сигма гл. <[сигма]доп.
2-ая теория прочности (теория максимальных относительных деформаций):При любом напр. сос-ии хрупкое разр. будет если макс. относит. дефор-ии достигнут пред. знач.
Условие разр-ия: епсилон max= епсилон пр.
ус-ие прочности: σэкв.=σ1-V(ню)*(σ2+σ3)<[σ]доп.
3-я теория прочности (теория максимальных касательных напряжений): При При любом напр. сос-ии пластич. разр. будет если макс касательные напряжения достигнут пред. состояния tmax = tпред., tmax=σ1-σ3/2, условие прочности: σэквIII= σ1— σ3≤ [σ]. Основной недостаток — не учитывает влияние s2.
При плоском напряженном состоянии: sэквIII= £ [s]. При sy=0 получаем Широко используется для пластичных материалов.
4-я теория прочности (энергетическая теория) При любом напр. состоянии разр. будет если удельная работа по изменению формы достигнет пред. значения.
σэкв=корень из{0.5*[(σ1-σ2)^2+(σ2-σ3)^2+(σ3-σ1)^2]}≤[σ]
Учитывает, все три главных напряжения.
Широко используется для пластичных материалов.
Теория прочности Мора Получена на основе кругов напряжений Мора. . Используется при расчетах хрупких материалов, у которых допускаемые напряжения на растяжение [sp] и сжатие [sс] не одинаковы (чугун).
Для пластичных материалов [sp]=[sс] теория Мора превращается в 3-ю теорию.
σэкв.=σ1-σв(+)/σв(-)*σ3≤[σ]
Круг Мора (круг напряжений). Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках. Откладываем от оси s из центра С луч под углом 2a (a>0, то против час.стр.), находим точку D,
координаты которой: sa,ta. Можно графически решать как прямую, так и обратную задачи.
Общий план решения задачи о проверки прочности:
Проверяем условие прочности ( Для хрупких материалов исп 1, 2 теорию прочности и Теорию прочности Мора; Для пластичных материалов 3ая и 4ая теория прочности)
Определяем действительный коэффициент запаса прочности.(n(действ.))
Находим опасное сечение.
для 1ой и 2 ой теор. Прочности: опасное сечение – это площадка перпендикулярная первому главному направлению
для 3ей и 4ой теор. Опасное сечение – плозадка на которой действ. Истинный максимум касательных напряжений. И для 4 оп.сеч – октаэдрическая площадка, т.е. равно наклоненная по всем 3ем осям.
Чистый и поперечный изгиб , типы опорных связей , определение спорных реакций. Внутренние усилия при плоском изгибе и связь между ними. Эпюры перерезывающих сил и изгибающих моментов. Дифференциальные зависимости между q, M и Q .
Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб.
Стержни, которые работают преимущественно на изгиб, называют балками (применяются в конструкциях зданий разнообразного назначения, мостах, в виде под крановых балок производственных зданий и т. д.). Они обладают простотой конструкции, изготовления и надежностью в работе.
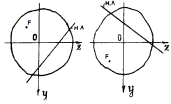
Виды опор.
Шарнирно'подвижная опора. Эта опора является устройством, допускающим перемещение опорного сечения параллельно опорной плоскости и поворот его в вертикальной плоскости относительно оси цилиндрического шарнира. Это устройство не дает возможности перемещаться в направлении наложенной связи по вертикали. Реакция шарнирно_подвижной опоры VA направлена вдоль опорной связи.
Шарнирно'неподвижная опора. Эта опора не допускает смещений опорного сечения ни в продольном, ни в поперечном направлениях, однако допускает поворот этого сечения относительно шарнира. Шарнирно неподвижная опора представляет собой опору с двумя связями, которые удобно прикладывать по направлению оси балки и перпендикулярно оси балки. В этой опоре появляются две составляющие опорной реакции: HA и VA.
Жесткое закрепление или заделка. Эта опора не допускает поворота опорного сечения и перемещения его ни в каком направ_лении — на это сечение наложены три связи: вертикальная VA, горизонтальная НА, составляющие опорной реакции, и изгибающий момент МА.
Если в балке сечением, имеющим вертикальную ось, внешняя нагрузка и реактивные усилия лежат в одной плоскости, совпадающей с осью сечения, то балка будетизгибаться в той же плоскости. Такой изгиб называют плоским.
Пусть при плоском изгибе внешняя нагрузка перпендикулярна продольной оси балки, тогда в поперечных сечениях балки возникают лишь поперечная сила и изгибающий момент, а продольная сила равна нулю. Такой изгиб называют поперечным.
Дифференциальные зависимости между q, M и Q .
1)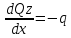
2)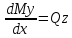
3)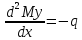
Нормальные напряжения при чистом изгибе – гипотеза плоских сечений, нейтральная ось, определение напряжений. Максимальные нормальные напряжения при изгибе, момент сопротивления сечения, равнопрочные балки.
Гипотеза плоских сечений: сечения, перпендикулярные оси стержня и плоские до деформации остаются такими же и после приложения нагрузки.
От действия изгибающего момента в поперечных сечениях балки возникают нормальные напряжения, определяемые по формуле
![]() ,где
М – изгибающий момент в рассматриваемом
сечении;
,где
М – изгибающий момент в рассматриваемом
сечении;
I – момент инерции поперечного сечения балки относительно нейтральной оси;
у – расстояние от нейтральной оси до точки, в которой определяются напряжения.
Из формулы (8.1), нормальные напряжения в сечении балки по ее высоте линейны, достигая максимального значения в наиболее удаленных точках от нейтрального слоя.
![]() ,где
W – момент сопротивления поперечного
сечения балки относительно нейтральной
оси. В
основе гипотезы
плоских сечений лежит
предположение, что и внутри стержня
деформации имеют
такой же характер, как на поверхности.
Следовательно, сечения, плоские и
нормальные к оси стержня до деформации,
остаются плоскими и нормальными к его
оси и после деформации. В этом и
заключается смысл
гипотезы плоских сечений.
,где
W – момент сопротивления поперечного
сечения балки относительно нейтральной
оси. В
основе гипотезы
плоских сечений лежит
предположение, что и внутри стержня
деформации имеют
такой же характер, как на поверхности.
Следовательно, сечения, плоские и
нормальные к оси стержня до деформации,
остаются плоскими и нормальными к его
оси и после деформации. В этом и
заключается смысл
гипотезы плоских сечений.
Нейтральная ось — линия в поперечном сечении изгибаемой балки, в точках которой нормальные напряжения, параллельные оси балки, равны нулю. Нейтральная ось делит сечение на две части, в одной из которых действуют растягивающие нормальные напряжения, а в другой — сжимающие.
Осевым
моментом сопротивления называется
отношение момента инерции относительно
данной оси к расстоянию от оси до наиболее
удаленной точки поперечного сечения
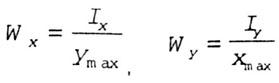
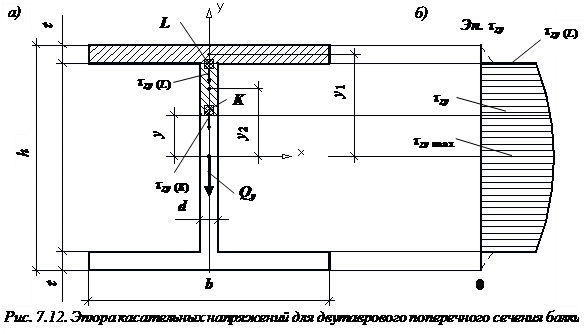
Касательное напряжение при изгибе. Формула Журавского. Эпюры касательных напряжений в прямоугольном и двутавровом сечении.
Касательное напряжение в любой точке поперечного сечения (рис. 2) определяется, как и парное напряжение, возникающее в продольном сечении, по формуле Журавского;Txz=
![]() ,где
,где ![]() -
поперечная сила в рассматриваемом
сечении;
-
поперечная сила в рассматриваемом
сечении;
![]() -
статический момент отсеченной части,b -
ширина поперечного сечения на уровне
исследуемой точки,
-
статический момент отсеченной части,b -
ширина поперечного сечения на уровне
исследуемой точки,
![]() -
момент инерции всего сечения относительно
нейтральной оси.
-
момент инерции всего сечения относительно
нейтральной оси.
Формула Журавского позволяет определить касательные напряжения при изгибе, возникающие в точках поперечного сечении балки, находящиеся на расстоянии от нейтральной оси x. Формула Журавского для касательных напряжений:
![]() ,
,
где Q — поперечная сила; S*x — статический момент отсечённой части поперечного сечения относительно оси х, F* — площадь отсечённой части поперечного сечения, yc — расстояние от центра отсечённой части поперечного сечения до оси х, Jx — главный осевой момент инерции полного сечения, by — ширина сечения в той точке, для которой находится напряжение.

Главные напряжения при изгибе. Теории прочности.
определим главные напряжения, выражая из через s и t:
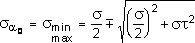
![]() .
σmax(min)=Mymax/Wy
.
σmax(min)=Mymax/Wy
1
теория прочности: ϭэквI
= ϭ1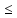 [ϭ]раст
[ϭ]раст
2
теория прочности: ϭIIэкв
= ϭ1-υ(ϭ2+ϭ3)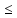 [
[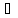 ]раст
]раст
теория
прочности Мора: ϭэквМ=ϭ1-ϭв+/ϭв-
*ϭ3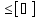 раст
раст
3
теория прочности: ϭэквIII=ϭ1-ϭ3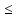 [ϭ]
[ϭ]
4
теория прочности:
ϭэквIV=корень(1/2[(ϭ1-ϭ2)^2+(ϭ2-ϭ3)^2+(ϭ3-ϭ1)^2])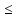 [ϭ]
[ϭ]
Дифференциальное уравнение изогнутой оси и его интегрирование. Определение произвольных постоянных. Определение перемещений.
Приблежённое диф. ур-ие EJyw̎=-My(x)
Начало отсчёта x выбираем на одном из торцов балки
Вычисления изгиб моментов запис для отсеч части , содер начало координат, при этом х отсчитывается от начала координат
Распред. нагрузка продлевается до конца балки, на тех участках балки где появилась фиктивная q прикладывается компенсир. нагрузка такого же закона и противополжная по напрвлению.
Произвольные постоянные опред. по граничным условиям. 1) Прогиб w(x=0)=0
Опред. перемещений :
Энергетич способ δ=1/EJy*∑My(xi)*M1(xi)dx
Сложное сопротивление. Формула для определения нормальных напряжений. Уравнение нейтральной линии. Касательные напряжения.
Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.
Наиболее часто в расчетной практике встречаются следующие виды сложного сопротивления:
· косой изгиб;
· внецентренное растяжение;
· изгиб с кручением.
При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.
Формула нормальных напряжений: σ max=Mрасч. max/Wy
![]() ,где
М – изгибающий момент в рассматриваемом
сечении;
,где
М – изгибающий момент в рассматриваемом
сечении;
I – момент инерции поперечного сечения балки относительно нейтральной оси;
у – расстояние от нейтральной оси до точки, в которой определяются напряжения.
Нейтральная линия – это геометрическое место точек, где отсутствуют нормальные напряжения.
Ϭх=My/Iy *z + Mz/Iz *y = 0.
Касательные напряжения: τxz=Qz*Syотс/b(z)*Iy
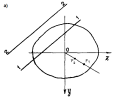
Косой изгиб. Определение напряжений и положения нейтральной линии. Определение перемещений.
Вид нагружения, когда плоскость действия нагрузки не совпадает не из одной из главных плоскостей но совпадает с центром тяжести
. Косой изгиб момента не совпадает ни с одной из глав. Под косым изгибом понимается такой случай изгиба, при котором плоскость изгибающего ных плоскостей инерции стержня.
Задачу косого изгиба сводят к одновременному рассмотрению двух плоских (прямых ) изгибов, раскрывая изгибающий момент в сечении на 2 момента, действуя в главных плоскостях (проходят через главные оси сечения) Т.к. напряжение от силы Q является второго напряжения порядка от изгиба.
Схема
сил при косом изгибе.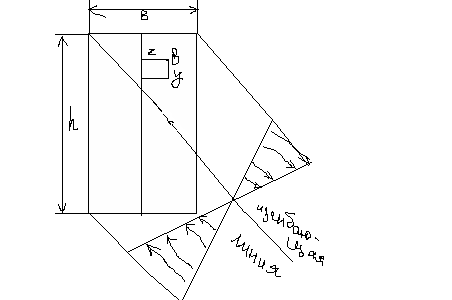
На рис. показан консольный стержень , нагруженный силой F, действующий перпендикулярно его оси и составляющей угол φ с главной плоскостью ху. Напряжение в некоторой точке В поперечного сечения на расстоянии х от незакрепленного торца. Моменты, изгибающие стержень в вертикальной и горизонтальной плоскостях х.
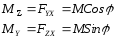
Где Fу и Fz - вертикаль и горизонталь, составляющие силы.
F,M- составляющие моменты в сечении
Напряжения
и нейтральная ось при косом изгибе.
Нормальное
напряжение в нейтральной точке с
координатами у и z
определяются суммой напряжений от
моментов Му и Мz
т.е.
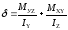
Максимальное
напряжение будет действовать в точках
наиболее удаленных от нейтральной
линии.
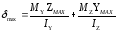
Положение
нейтральной линии при косом изгибе
найдем из уравнения полога δ=0 обозначая
координаты нейтральной линии Y0 и Z0
получим
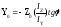
Видно
что нейтральная линия является прямой
проходящей через начало координат
(центр тяжести поперечного сечения)
обозначая через α угол наклона нейтральной
линии к оси Z найдем
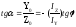
Определение перемещений при косом изгибе
Перемещения
при косом изгибе определяют по принципу
независимости действия сил, т.е.
рассчитывают прогибы
![]() в направлении главных осей, а величину
полного прогиба в любом сечении балки
получают геометрическим суммированием:
в направлении главных осей, а величину
полного прогиба в любом сечении балки
получают геометрическим суммированием:![]() .
.
Например, для балки, изображенной на рис.7.13, прогиб конца консоли определится следующим образом:
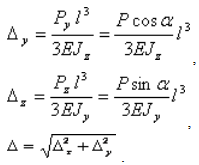
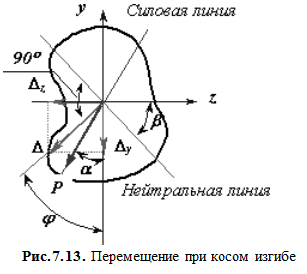
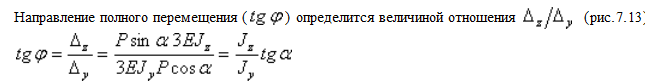
Направление полного прогиба при косом изгибе перпендикулярно нейтральной линии и не совпадает с направлением внешней силы (рис.7.13).
При косом изгибе (впрочем, как и при остальных видах нагружения) имеем три задачи расчета на прочность:
1) проверка прочности;
2) подбор сечения [определить Wz (размеры сечения), при заданном отношении Wz/Wy];
3) проверка по несущей способности (определить M).
Порядок проверки прочности балки, работающей в условиях косого или пространственного изгиба, тот же, что и для балки, работающей при плоском поперечном изгибе. Для этого необходимо:
- построить эпюры внутренних усилий (изгибающих моментов). Для построения эпюр внутренних усилий раскладываем нагрузки на вертикальную и горизонтальную составляющие. Вертикальная составляющая вызывает изгиб относительно горизонтальной оси , горизонтальная – относительно оси ;
- выбрать опасные сечения – это сечения, где имеет место наиболее неблагоприятное сочетание изгибающих моментов;
- в опасных сечениях найти опасные точки – точки с максимальными нормальными напряжениями;
- записать условие прочности в этих точках. Из условия прочности либо подобрать размеры поперечного сечения, либо найти допускаемую нагрузку, либо просто сделать вывод о возможности безопасной эксплуатации конструкции.
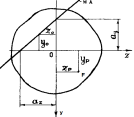
Внецентренное растяжение(сжатие). Ядро сечения. Свойства нейтральных линий.
Внецентренное растяжение (сжатие) – нагружение, при котором брус растя-гивается силами, параллельными его оси и не проходящими через центр тя-жести сечения бруса. σx=N/A+My*z/Jy+Mz*y/Jz
Точку P приложения силы при внецентренном растяжении (сжатии) будем называть полюсом силы. При этом расстояние от полюса P до продольной оси стержня (Ox) именуется эксцентриситетом.
Ядро сечения.
Ядро сечения –мнимая область вокруг центра тяжести сечения, при приложении си-лы внутрь которой, в сечении возникают напряжения одного знака.
Чтобы
построить очертания (контур) ядра
сечения, необходимо: 1) задать несколько
положений нейтральной оси так, чтобы
она лишь касалась контура сечения, но
не пересекала его ни в од-ной точке; 2)
определить для каждого из этих положений
координаты yн
и
zн
точек
пересечения нейтральной линии с осями
Oy
и
Oz;
3) вычислить для ка-ждого положения
нейтральной оси ко-ординаты точки
приложения силы (yp
и
zp)
по формулам y
н=-iz^2/yf
и z
н=-iy^2/zf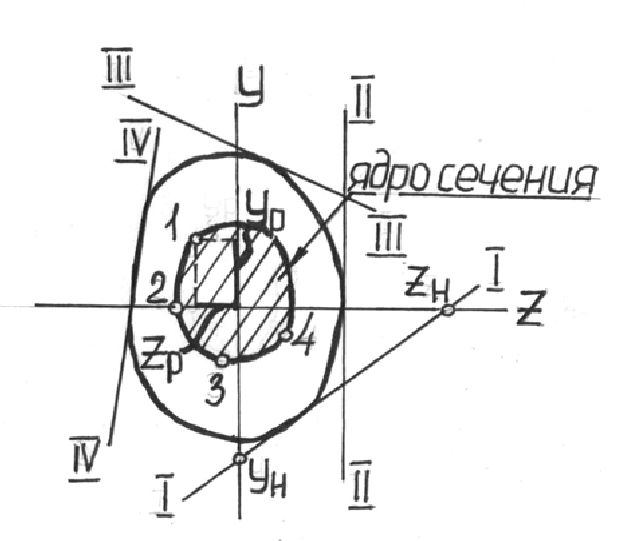
Свойства нейтральных линий
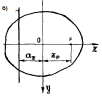
Нейтральная ось (нейтральная линия) — линия в поперечном сечении изгибаемой балки, в точках которой нормальные напряжения, параллельные оси балки, равны нулю. Нейтральная ось делит сечение на две части, в одной из которых действуют растягивающие нормальные напряжения, а в другой — сжимающие.
Св-ва:1) положение н.л. не зависит от значения силы, а зависит толко от места приложения.
2) н.л всегда проходит через квадрант противоположный точке приложения силы .Место приложения наз. полюсом
3) Если полюс лежит на одной из главных осей то н.л. пройдет параллельно главной оси.
4) Если полюс приблежается к центру тяжести то н.л. удаляется от него.
5) Если полюс движется по прямой ,проходящей через центр тяжести то н.л. будут паралл. между собой.
6) Если полюс движ не через центр то все н.л. будут проходит через (.)
Установим характерные свойства взаимного расположения нейтральной линии и центра давления:
центр давления и нейтральная линия расположены в противоположных квадрантах (рис. 13.5);
|
|
|
Рис. 13.5 Взаимное расположение нейтральной линии и центра давления
если центр давления приближается к центру тяжести по прямой, то нейтральная линия удаляется от него, оставаясь параллельной самой себе (при
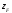 =0,
=0,
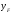 =0
=0
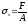 ,
,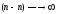 );
);если центр давления лежит на одной из главных осей инерции, то нейтральная линия параллельна другой оси;
|
|
|
Рис. 13.6 Центр давления перемещается вдоль центральной прямой или расположен на главной оси инерции
4)если центр давления перемещается по прямой не проходящей через центр тяжести, то нейтральная линия поворачивается вокруг некоторой точки.

Рис. 13.7 Центр давленияперемещается вдоль прямой, не проходящей через центр тяжести, n-n поворачивается вокруг точки D
Совместное действие изгиба и кручения.
Кручение с изгибом - вид нагружения, при котором брус подвергается одновременно действию скручивающих и изгибающих моментов, называется изгибом с кручением.

При расчете воспользуемся принципом независимости действия сил. Определим напряжения по отдельности при изгибе и кручении.
При изгибе в поперечном сечении возникают нормальные напряжения, достигающие максимального значения в крайних волокнах
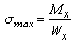
При кручении в поперечном сечении возникают касательные напряжения, достигающие наибольшего значения в точках сечения у поверхности вала
![]()
Нормальные и касательные напряжения одновременно достигают наибольшего значения в точках А и В сечения вала (рис.7.6).
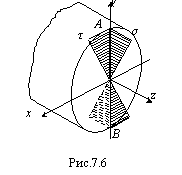
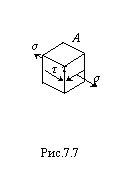
Рассмотрим напряженное состояние в т.А (рис.7.7). Видно, что элементарный параллелепипед, выделенный вокруг т.А, находится при плоском напряженном состоянии. Поэтому для проверки прочности применим одну из гипотез прочности.
Условие прочности по третьей гипотезе прочности (гипотезе наибольших касательных напряжений)
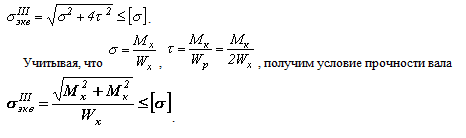
Если изгиб вала происходит в двух плоскостях, то условие прочности
будет
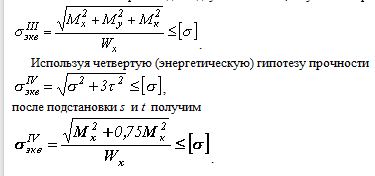
Закон сохранения энергии . Вычисление потенциальной энергии. Теорема Клапейрома.
Кроме рассмотренных способов вычисления прогибов и углов поворота сечений балок существует более общий метод, пригодный для определения деформаций любых упругих конструкций. Он основан на применении закона сохранения энергии.
При статическом растяжении или сжатии упругого стержня происходит превращение потенциальной энергии из одного вида в другой; часть потенциальной энергии действующего на стержень груза полностью переходит в потенциальную энергию деформации стержня. Действительно, если мы будем нагружать стержень путем постепенного подвешивания к его нижнему концу очень малых грузов dP, то при добавлении каждого такого груза подвешенная уже часть нагрузки опустится и ее потенциальная энергия уменьшится, а потенциальная энергия деформации стержня соответственно увеличится.
Это явление имеет место при любом виде деформации всякой упругой конструкции при статической нагрузке; такую конструкцию можно рассматривать как своеобразную машину, преобразующую один вид потенциальной энергии в другой.
Мы условились называть «статической» такую нагрузку, которая возрастает постепенно и таким образом, что ускорениями элементов конструкции можно пренебречь; передача давлений (сил) от одной части конструкции на другую не меняет характера движения, этих частей, т. е. их скорость остается постоянной и ускорение отсутствует.
При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой. При этом мы пренебрегаем магнитными, электрическими и тепловыми явлениями, сопровождающими упругие статические деформации тела лишь в очень слабой мере.
Так как характер движения всех элементов конструкции с течением времени не меняется, то в каждый момент времени будет иметь место равновесие как для каждой части конструкции в целом под действием внешних сил и реакций, так и для каждого элемента этой части под действием внешних сил и напряжений, приложенных к этому элементу. Деформации конструкции, напряжения в ее частях и реакции, передающиеся от одной части на другую, успевают следовать за ростом нагрузки.
Таким образом, можно сказать, что полное преобразование одного вида потенциальной энергии в другой имеет место, если деформация происходит без нарушения равновесия системы. Мерой энергии, превратившейся в другой вид, является величина работы, произведенной силами, действующими на конструкцию.
Обозначим
величину накопленной потенциальной
энергии деформации через U,
а уменьшение потенциальной энергии
внешних нагрузок ![]() .
Тогда величина
.
Тогда величина![]() измеряетсяположительной работой
этих нагрузок
измеряетсяположительной работой
этих нагрузок ![]() ,
с другой стороны, накоплению потенциальной
энергии деформацииU соответствует отрицательная работа
внутренних, междучастичных сил А,
так как перемещения точек тела при
деформации происходят в обратном по
отношению к внутренним силам направлении.
,
с другой стороны, накоплению потенциальной
энергии деформацииU соответствует отрицательная работа
внутренних, междучастичных сил А,
так как перемещения точек тела при
деформации происходят в обратном по
отношению к внутренним силам направлении.
Закон сохранения энергии при деформациях упругих систем принимает вид:
![]()
заменяя
в этой формуле величины ![]() иU
численно равными
им значениями работ
иU
численно равными
им значениями работ ![]() и
—А, получаем иную формулировку этого
закона:
и
—А, получаем иную формулировку этого
закона:
![]() или
или ![]()
Эта формулировка закона сохранения энергии совпадает с так зазываемым «началом» возможных перемещений в применении к упругим системам. Последнее равенство выражает, что при перемещениях без нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна нулю.
Таким образом, начало возможных перемещений в применении к упругим системам является следствием закона сохранения энергии.
Таким
образом, потенциальная энергия
деформации ![]() численно равна
работе внешних сил
численно равна
работе внешних сил ![]() ,
проделанной ими этой деформации:
,
проделанной ими этой деформации:
![]()
Вычисление потенциальной энергии.
При вычислении потенциальной энергии будем предполагать, что деформации не только материала, но и всей конструкции, следуя закону Гука, пропорциональны нагрузкам, т. е.линейно с ними связаны и растут постепенно вместе с ними.
Известно,
что при статическом растяжении или
сжатии стержня силами Р величина
работы ![]() ,
а следовательно, и величина
энергииU равняется:
,
а следовательно, и величина
энергииU равняется:
![]()
В случае сдвига
![]()
При кручении
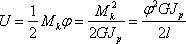
Так же как и при кручении, может быть вычислена потенциальная энергия при чистом изгибе.
Концевые
сечения балки под действием изгибающих
моментов(Рис.1) повернутся на угол ![]() ,
где
,
где![]() —
центральный угол изогнувшейся по дуге
радиусомр оси
балки.
—
центральный угол изогнувшейся по дуге
радиусомр оси
балки.
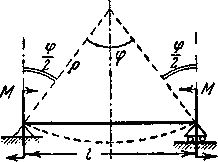 Рис.1. Модель
расчета потенциальной энергии при
чистом изгибе.
Рис.1. Модель
расчета потенциальной энергии при
чистом изгибе.
Тогда
![]()
так
как из общей теории изгиба ![]() а
а![]()
Из полученных выражений следует, что потенциальная энергия деформации равна половине произведения силы или пары сил на перемещение по ее направлению того сечения, где эта сила приложена. Условимся называть термином «обобщенная сила» всякую нагрузку, вызывающую соответствующее нагрузке перемещение, т. е. и сосредоточенную силу, и пару сил, и т. п.; перемещение же, соответствующее этой силе, будем называть «обобщенной координатой».
«Соответствие» заключается в том, что речь идет о перемещении того сечения, где приложена рассматриваемая сила, причем о таком перемещении, что произведение его на эту силу дает нам величину работы; для сосредоточенной силы это будет линейное перемещение по направлению действия силы — прогиб, удлинение; для пары сил — это угол поворота сечения по направлению действия пары.
Иначе: потенциальная энергия деформации численно равна половине произведения обобщенной силы на соответствующую ей координату.
![]() ,
,
где Р—обобщенная
сила, ![]() —
обобщенная координата.
—
обобщенная координата.
Полученные соотношения также показывают, что потенциальная энергия является функцией второй степени от независимых внешних сил, так как в эти формулы не входят реакции, зависящие от приложенных к элементу сил и связанные с ними уравнениями равновесия. Из тех же формул видно, что величина потенциальной энергии деформации является функцией второй степени от «обобщенных координат» системы и вполне ими определяется. Таким образом, порядок приложения нагрузок в этом отношении безразличен, важна лишь окончательная форма деформированного элемента. Поэтому, хотя результаты этого параграфа получены в предположении, что нагрузка возрастает статически, при сохранении равновесия в течение всего процесса нагружения, однако выведенные формулы сохраняют силу и при любом способе приложения нагрузок, лишь бы значения сил и деформаций были связаны линейной зависимостью и относились к тому моменту, когда установится равновесие конструкции.
Известно также, что в общем случае изгиба изгибающий момент М(х) является величиной переменной. В любом сечении ему будет сопутствовать поперечная сила Q(х). Поэтому рассматривать следует уже,не всю балку в целом, а лишь бесконечно малый элемент балки длиной dx.
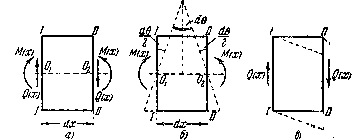 Рис.2. Энергетическая
модель поперечного изгиба
Рис.2. Энергетическая
модель поперечного изгиба
Под
действием изгибающих усилий сечения
элемента (рис.2, а) поворачиваются и
образуют между собой угол ![]() (Рис.2,б).
Касательные же усилия стремятся вызвать
(Рис.2, в)
перекос элемента; таким образом
перемещения от нормальных напряжений
идут перпендикулярно к направлению
касательных напряжений, и наоборот.
(Рис.2,б).
Касательные же усилия стремятся вызвать
(Рис.2, в)
перекос элемента; таким образом
перемещения от нормальных напряжений
идут перпендикулярно к направлению
касательных напряжений, и наоборот.
Это позволяет независимо вычислять работу изгибающих и касательных усилий.
Обычно работа касательных усилий оказывается малой по сравнению с работой нормальных, поэтому мы пока ею будем пренебрегать. Элементарная работа нормальных усилий (как и в случае чистого изгиба) равна:
![]()
или
![]()
 Рис.3. Расчетная
схема примера расчета потенциальной
энергии при поперечном изгибе.
Рис.3. Расчетная
схема примера расчета потенциальной
энергии при поперечном изгибе.
Вся потенциальная энергия изгиба получится суммированием по длине балки
![]()
Знак предела интегрирования условно указывает, что интегрирование должно охватить всю балку; в тех случаях, когда для М(х) мы имеем несколько участков, то интеграл приходится разбивать на сумму интегралов.
Вычислим потенциальную энергию балки на двух опорах, нагруженной силой Р (Рис.3). Эпюра моментов имеет два участка; поэтому

![]()
![]()
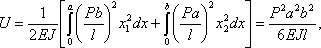
Формулировка теоремы Клапейрона: Потенциальная энергия упругой деформации тела численно равна полусумме произведений обобщ. силы(есть любое силовое воздействие на стежнь) на соотв. обобщ. перемещние(перемещение соотвтств. обобщ. силе) , при этом зависимость между обощ. силами и перемещениями линейная. U(c черточками)=1/2∑FобUоб
упругая работа внешней силы при статическом приложении равна половине произведения ее окончательного значения на соответствующее этой силе перемещение.
Теорема Клапейрона впервые была сформулирована французским ученым Клапейроном в 1852 г.
Определим
работу, которую совершает сила ![]() ,
действующая, например, на балку,
изображенную на рис. 15.1, а.
,
действующая, например, на балку,
изображенную на рис. 15.1, а.
Будем
считать, что нагрузка прикладывается
к балке статически, то есть она медленно
возрастает от нуля до заданной величины![]() .
.
Пусть
в некоторый момент сила, достигшая
значения ![]() ,
вызвала в месте своего приложения прогиб
балки, равный
,
вызвала в месте своего приложения прогиб
балки, равный ![]() .
.
Увеличим
это значение силы на бесконечно малую
величину ![]() .
Такое изменение нагрузки приведет к
дополнительному прогибу
.
Такое изменение нагрузки приведет к
дополнительному прогибу ![]() .
Очевидно, что элементарная дополнительная
работа будет равна:
.
Очевидно, что элементарная дополнительная
работа будет равна: ![]() .
.
Полная
работа, совершенная внешней силой,
определяется по формуле: 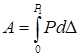 .Для
линейно деформируемой системы (график
зависимости между прогибом
.Для
линейно деформируемой системы (график
зависимости между прогибом ![]() и
силой P для такой системы показан на
рис. 15.1, б) прогиб балки пропорционален
внешней нагрузке, то есть
и
силой P для такой системы показан на
рис. 15.1, б) прогиб балки пропорционален
внешней нагрузке, то есть ![]() ,
,
где ![]() –
коэффициент пропорциональности или
перемещение от силы, равной единице
–
коэффициент пропорциональности или
перемещение от силы, равной единице ![]() .
Коэффициент
.
Коэффициент ![]() часто
называют и податливостью системы.
часто
называют и податливостью системы.
Дифференцируя
уравнение ![]() ,
найдем:
,
найдем: ![]() .
.
Подставляя
формулу ![]() в
формулу
в
формулу  и
учитывая уравнение
и
учитывая уравнение ![]() ,
получим:
,
получим: 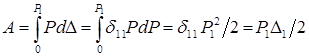 ,что
и требовалось доказать. Полученное
выражение соответствует теореме
Клапейрона
,что
и требовалось доказать. Полученное
выражение соответствует теореме
Клапейрона
Вычисление потенциальной энергии стержней при растяжении – сжатии, кручении, изгибе и сложном сопротивлении.
Согласно закону сохранения энергии, работа внешних сил не исчезает, а переходит в потенциальную энергию (V), накапливаемую в упругом теле при его деформировании.
Следовательно, потенциальная энергия деформации численно равна работе внешних сил при нагружении тела (или работе внутренних сил, совершаемой ими в процессе разгружения).
Таким образом, потенциальная энергия деформации стержня, испытывающего, например, растяжение, кручение и прямой поперечный изгиб, равна:
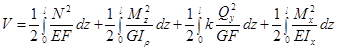 .
.
Как видно из этой формулы, потенциальная энергия деформации всегда положительна, поскольку она является квадратичной функцией обобщенных сил (или обобщенных перемещений, так как последние линейно связаны с обобщенными силами). Отсюда следует, что потенциальная энергия, накопленная в результате действия группы сил, не равна сумме потенциальных энергий, накопленных от действия каждой нагрузки в отдельности. То есть принцип независимости действия сил при вычислении потенциальной энергии деформации не применим.
Потенциальная энергия стержня при растяжении – сжатии и изгибе: U1=ϭ2/2E
(НЕ УВЕРЕН) U=∑Ni*li/2Ei*Ai
Кручение:
Элементарная
работа статически приложенного внешнего
момента Т на
перемещении ![]() равна:
равна:
![]() .
.
При
чистом кручении Мк = Т и ![]() .
.
Потенциальная энергия деформации
![]() ;
;
интегрируя выражение для элементарной работы по всей длине l стержня, получим
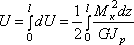 .
.
При Мк = const и ![]() =const,
получим
=const,
получим
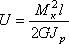 .
.
Сложное сопротивление: кручение+растяж+∑(∫Midx/dEiJyi+Kф∫Qi^2dx/2GiAi)
![]()
При простом растяжении (s2=s3=0)
![]()
Теорема Кастильяно. Определение перемещений в статически определимых системах.
Частная производная от потенциальной энергии упругой деформации тела по обобщённой силе равна соотвтсвующему обобщ перемещению.
ai=∑N/EiAi *dN/dFi + ∑Mкр/GiJроi *dMкр/dFi + ∑(∫Mi/EiJyi *dMi/dFi *dx + Кф∫Qi/GiAi * dQi/dFi *dx)
Интеграл Мора δ=∫My(x)Mштрих(x)/EJy * dx
Формула Максвелла – Мора для определения перемещений в упругих стержневых системах. Правило Верещагина.