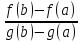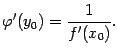- •Элементы линейной алгебры
- •1. Операции над матрицами. Свойства операций.
- •2. Определители 2-го и 3-го порядков. Минор и алгебраическое дополнение. Определитель n-го порядка. Свойства определителей.
- •3. Обратная матрица. Теорема существования обратной матрицы.
- •4. Системы линейных уравнений. Матричная запись системы. Формулы Крамера.
- •5. Однородная система линейных уравнений и свойства ее решений.
- •6. Решение систем методом Гаусса.
- •Векторная алгебра
- •7. Линейные операции над векторами. Базис.
- •8. Проекция вектора на ось. Прямоугольная система координат. Координаты точки. Линейные операции над векторами в координатной форме.
- •9. Скалярное произведение векторов, его свойства. Вычисление в координатах.
- •10. Определение правой тройки векторов. Векторное произведение векторов, его свойства, геометрический смысл.
- •11. Смешанное произведение 3-х векторов, его свойства. Геометрический смысл. Вычисление в координатах. Необходимое и достаточное условие компланарности 3-х векторов.
- •16. Виды уравнений прямой в пространстве. Расстояние от точки до прямой.
- •17. Взаимное расположение двух прямых в пространстве, угол между прямыми.
- •18. Взаимное расположение прямой и плоскости, угол между ними.
- •19. Каноническое уравнение эллипса, эксцентриситет, директриса.
- •20. Канонические уравнение гиперболы, эксцентриситет, директриса, асимптоты.
- •21. Каноническое уравнение параболы
- •27. Основные элементарные функции и их графики.
- •28. Предел числовой последовательности. Бесконечно большие и бесконечно малые числовые последовательности. Свойства бесконечно малых.
- •29. Основные теоремы о пределах последовательностей.
- •30. Первый и второй замечательные пределы. Число е.
- •31. Предел функции. Основные теоремы о пределах функций.
- •32. Замечательные пределы для функций.
- •33. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •34. Непрерывные функции. Классификация точек разрыва.
- •35. Свойства непрерывных функций. Основные теоремы о непрерывных функциях.
- •36. Определение производной, ее геометрический смысл.
- •37. Дифференцируемость и непрерывность. Правила дифференцирования.
- •38. Производная сложной функции, функции, заданной неявно, заданной параметрически, обратной функции.
- •39. Производные основных элементарных функций.
- •41. Производные и дифференциалы высших порядков.
- •42. Теорема Ферма. Теорема Ролля.
- •43. Теорема Лагранжа и следствия из нее. Теорема Коши.
- •44. Правило Лопиталя.
- •45. Возрастание и убывание дифференцируемой функции. Необходимые и достаточные условия.
- •46. Экстремум дифференцируемой функции. Необходимые и достаточные условия.
- •47. Теорема (второе достаточное условие экстремума).
- •48. Выпуклость функции. Необходимые и достаточные условия выпуклости. Точки перегиба.
- •49. Асимптоты графика функций.
38. Производная сложной функции, функции, заданной неявно, заданной параметрически, обратной функции.
Пусть y=f(u) – дифференцируема в uo, u=g(x)- дифференцируема в xo, uo = g(xo), тогда сложная функция y = f(g(x)) дифференцируема в xo и y`= f `(g(x)*g`(x))
Функция задана неявно, если она задана уравнением f(x,y) = 0 не разрешённым относительно y.
Для нахождения производной y`x от неявно заданной функцией F(x,y) = 0 достаточно продифференцировать это уравнение по x, рассматривать y, как функцию от x и полученное уравнение решить относительно y`.
Пусть x(t), y(t) – дифференц, ф x(t) имеет обратную функцию t = t(x). Тогда y` = y(t(x))
y`x
= y`t
*
t`x
=

Пусть
функция
![]() имеет
в точке
имеет
в точке![]() производную
производную![]() .
Тогда обратная функция
.
Тогда обратная функция![]() имеет
в соответствующей точке
имеет
в соответствующей точке![]() производную
производную![]() ,
которую можно отыскать по формуле
,
которую можно отыскать по формуле
|
|
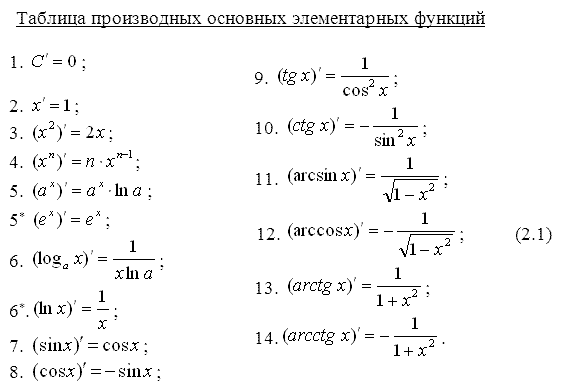
39. Производные основных элементарных функций.
40. Дифференциал. Формула df(x) = f `(x)dx.
Если приращение функции ∆f(x) = A*∆x + 0(∆x), где A=const, 0(∆x) – бесконечно малая, более высокого порядка, чем ∆x, то говорят, что f(x) имеет дифференциал в точке x и он равен главной линейной части приращения A*∆x.
Теорема: если f(x) дифференцируема в точке x, то df(x) = f `(x)dx
Доказательство:
∆f(x) = A*∆x + 0 (∆x)
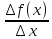 =
A +
=
A +
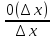
f
`(x) =
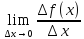 =
=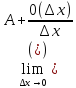 = A,т.е.
A = f `(x)
= A,т.е.
A = f `(x)
df(x) = f `(x)*∆x
возьмём f(x)= x
dx = x`∆x = ∆x, т.е. ∆x = dx
df(x) = f `(x)dx
из
формулы f
`(x)
=

41. Производные и дифференциалы высших порядков.
Производной
n-го
порядка от функции ![]() называется производная от производной
(n - 1)-го
порядка:
называется производная от производной
(n - 1)-го
порядка:
![]()
Производная второго порядка: ![]()
df(x) =f`(x)dx
d2f(x) =d(df(x)) =d(f`(x)dx) = (f`(x)dx)`dx=f``(x)dxdx+f`(x)(dx)`dx=f``(x)(dx)2
f``f(x) =d(dn-1 f(x))
Формула для вычисления дифференциала n–го порядка
|
|
dn f(x) = f(n) (x) dxn . |
42. Теорема Ферма. Теорема Ролля.
Теорема Ферма: Пусть f(x) непрерывная функция на [a,b], xo принадлежит [a,b] – точка экстремума, существует f `(xo). Тогда f `(xo) = 0
Доказательство: Пусть xo – точка максимума => существует b > 0: f(x) ≤ f(xo). Любой x принадлежит (xo – b, xo + b)
Если x принадлежит (xo – b, xo), то ∆x = x – xo ≤ 0
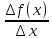 =
=
 ≥ 0
≥ 0
Если x принадлежит (xo; xo + b), то ∆x ≥ 0
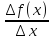 =
=
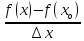 ≤ 0
≤ 0
т.к.
существует f
`(x),
то существует
 =f
`(xo)
≤ 0
=f
`(xo)
≤ 0
существует
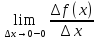 =f
`(xo)
≥ 0
=f
`(xo)
≥ 0
=> f `(xo) = 0.
Теорема Ролля: Если f(x) – непрерывна на отрезке [a,b], f(a) = f(b), f(x) – дифференцируема на (a,b), то существует xo , принадлежащий [a,b]: f `(xo) = 0
Доказательство: т.к. f(x) – непрерывна на [a,b], то по теореме о непрерывных функциях существует максимальное M и минимальное m значение f(x). Если m=M, то f(x)=const. f `(x) = 0.
43. Теорема Лагранжа и следствия из нее. Теорема Коши.
Теорема Лагранжа: Если f(x) – непрерывна на [a,b], f(x) – дифференцируема на (a,b), то существует xo , принадлежащий (a,b): f(b) – f(a) = f `(xo)(b - a)
Следствие 1: Если f `(x) = 0 любой x, принадлежащий [a,b], то f(x) = const.
Следствие 2: Если для любого x, принадлежащего (a,b) значение производной > 0, то эта функция возрастает на интервале (a,b). Если значение производной < 0, то убывает.
Следствие 3: Пусть X - некоторый промежуток, и значения производной на этом промежутке ограничены числом C: |f`(x)| ≤C. Тогда функцияf(x) равномерно непрерывна на данном промежутке.
Теорема
Коши: Если f(x),
g(x)
– непрерывны на [a,b].
f(x),
g(x)
дифференцируемы на (a,b)
g`(x)≠ 0, любойxпринадлежит
(a,b), то
существуетxo, принадлежащее (a,b):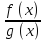 =
=