34. Непрерывные функции. Классификация точек разрыва.

Функция f(x) называется непрерывной в точке x_o, если:

1) f(x) определена в окрестность x_o

2) существует =f(x₀)

Замечание 1: условие 2 эквивалентно = f()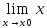

Замечание 2: обозначим через ∆f (x_o) = f (x_o + ∆x) – f(x_o) приращение функции f(x) при приращении аргумента ∆x = x - x_o

Тогда определение 1 перепишется в виде: = 0

Точка x₀, в которой нарушается непрерывность, называется точкой разрыва.

Точка разрыва x₀ называется точкой разрыва 1-го рода функции f(x), если выполнено хотя-бы одно из условий:

1) Существует 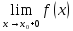=A ₊ < ∞

Существует =A _- < ∞

A ₊ = A _- => точка устранимого разрыва

2) A ₊ ≠A _- => x₀ точка конечного разрыва

Если хотя-бы один из пределов 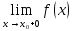или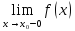не существует, или бесконечен, то точкаx₀ называется точкой разрыва 2-го порядка.

35. Свойства непрерывных функций. Основные теоремы о непрерывных функциях.

Свойства функций, непрерывных в точке:

1) Сумма, разность и произведение двух функций, непрерывных в точке x = a, непрерывны в этой точке.

2) Если функция f(x) непрерывна при некотором значении x, то приращение функции бесконечно мало при бесконечно малом приращении аргумента.

Свойства функции, непрерывных на замкнутом промежутке:

1) Среди значений, которые принимает функция f(x) в точках незамкнутого промежутка (a,b), может не быть наибольшего или наименьшего.

2) Если m есть значение функции f(x) при x = a и n – значение f(x) при x=b, то функция f(x) принимает внутри промежутка (a,b) по крайней мере по одному разу всякое значение p, заключенное между m и n.

3) Если переменные x и x` изменяются так, что разность x – x` бесконечно малая, то разность f(x) – f (x`) тоже бесконечно малая.

Теоремы:

1) Если f(x),g(x) – непрерывны вx₀, тоc*f(x), гдеc– действительное число,f(x) +g(x),f(x)*g(x),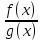(g(x₀) ≠ 0), - непрерывные функции вx₀

Если y=f(u) – непрерывна вu₀,u=(x) – непрерывна вx₀,(x₀) =u_o , то композиция функцииy=f((x)) непрерывна в x_о

2) Все элементарные функции непрерывны в своей области определения

3) Функция, непрерывная на отрезке достигает своего минимума и максимума значений

4) Функция, непрерывная на отрезке принимает все промежуточные значения

f(a) =A,f(b) =B,A<B,f(x) – непрерывна на [a,b] =>любоеcпринадлежит [A,B] => существуетx₀принадлежит [a,b]f(x₀) =c

36. Определение производной, ее геометрический смысл.

Пусть функция y = f (x) определена в некоторой окрестности точки x_ои существует конечный предел отношения. Тогда этот предел называется производной функции в точке x_о

Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции y=f(x)  в точке  x_o  равен производной функции

y=f(x) в этой точке:

37. Дифференцируемость и непрерывность. Правила дифференцирования.

Функция y=f(x) называется дифференцируемой в точке x_o , если ее приращение Δy в точке x_oможет быть представлено в виде: Δy = A*Δx + α(Δx) * Δx, где A - некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е.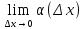= 0.

ТеоремаДля того, чтобы функция y=f(x) быладифференцируема в точке x_o, необходимо и достаточно, чтобы она в этой точке имела конечную производную.

Говорят, что функция f (x) является непрерывной в точке a (a – действительное число), если для любой последовательности {x_n}, такой, что

выполняется соотношение

Правила дифференцирования:

1) (c*f(x))` = c * f `(x)

2) (f(x) ± g(x))` = f `(x) ± g` (x)

3) (f(x) * g(x))` = f `(x) * g (x) + f (x) * g`(x)

4) )` =
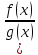