
- •Элементы линейной алгебры
- •1. Операции над матрицами. Свойства операций.
- •2. Определители 2-го и 3-го порядков. Минор и алгебраическое дополнение. Определитель n-го порядка. Свойства определителей.
- •3. Обратная матрица. Теорема существования обратной матрицы.
- •4. Системы линейных уравнений. Матричная запись системы. Формулы Крамера.
- •5. Однородная система линейных уравнений и свойства ее решений.
- •6. Решение систем методом Гаусса.
- •Векторная алгебра
- •7. Линейные операции над векторами. Базис.
- •8. Проекция вектора на ось. Прямоугольная система координат. Координаты точки. Линейные операции над векторами в координатной форме.
- •9. Скалярное произведение векторов, его свойства. Вычисление в координатах.
- •10. Определение правой тройки векторов. Векторное произведение векторов, его свойства, геометрический смысл.
- •11. Смешанное произведение 3-х векторов, его свойства. Геометрический смысл. Вычисление в координатах. Необходимое и достаточное условие компланарности 3-х векторов.
- •16. Виды уравнений прямой в пространстве. Расстояние от точки до прямой.
- •17. Взаимное расположение двух прямых в пространстве, угол между прямыми.
- •18. Взаимное расположение прямой и плоскости, угол между ними.
- •19. Каноническое уравнение эллипса, эксцентриситет, директриса.
- •20. Канонические уравнение гиперболы, эксцентриситет, директриса, асимптоты.
- •21. Каноническое уравнение параболы
- •27. Основные элементарные функции и их графики.
- •28. Предел числовой последовательности. Бесконечно большие и бесконечно малые числовые последовательности. Свойства бесконечно малых.
- •29. Основные теоремы о пределах последовательностей.
- •30. Первый и второй замечательные пределы. Число е.
- •31. Предел функции. Основные теоремы о пределах функций.
- •32. Замечательные пределы для функций.
- •33. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •34. Непрерывные функции. Классификация точек разрыва.
- •35. Свойства непрерывных функций. Основные теоремы о непрерывных функциях.
- •36. Определение производной, ее геометрический смысл.
- •37. Дифференцируемость и непрерывность. Правила дифференцирования.
- •38. Производная сложной функции, функции, заданной неявно, заданной параметрически, обратной функции.
- •39. Производные основных элементарных функций.
- •41. Производные и дифференциалы высших порядков.
- •42. Теорема Ферма. Теорема Ролля.
- •43. Теорема Лагранжа и следствия из нее. Теорема Коши.
- •44. Правило Лопиталя.
- •45. Возрастание и убывание дифференцируемой функции. Необходимые и достаточные условия.
- •46. Экстремум дифференцируемой функции. Необходимые и достаточные условия.
- •47. Теорема (второе достаточное условие экстремума).
- •48. Выпуклость функции. Необходимые и достаточные условия выпуклости. Точки перегиба.
- •49. Асимптоты графика функций.
27. Основные элементарные функции и их графики.
1)
1) y = xn,
n > 1

2)
y =
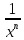
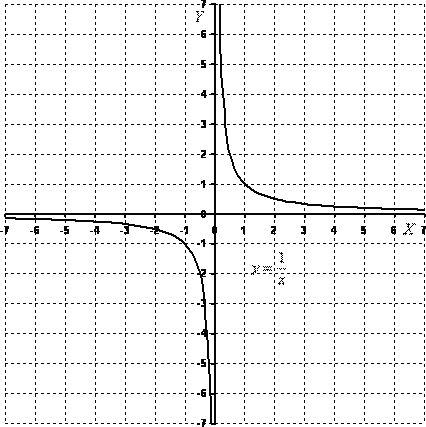
3)
y =
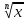 ,
n > 1
,
n > 1
2) y =
ax 
1) a >1
2) 0 < a < 1
3) y
= log a
x 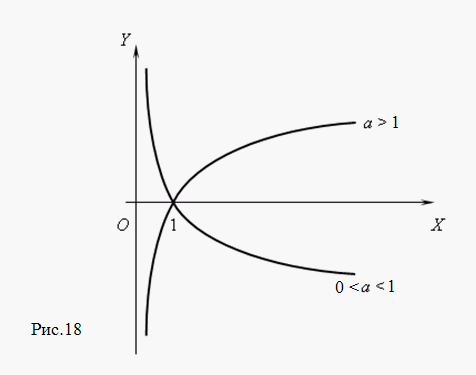
1) a > 1
2) 0 < a < 1
4) y = sin x , cos x, tg x, ctg x
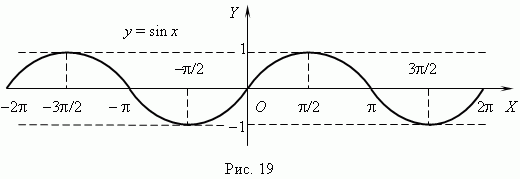
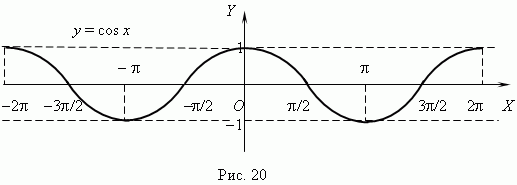
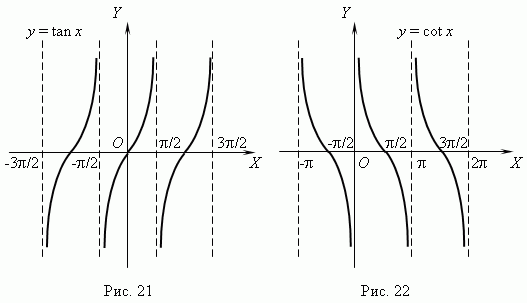
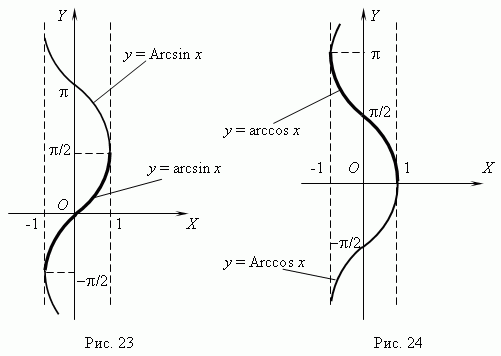
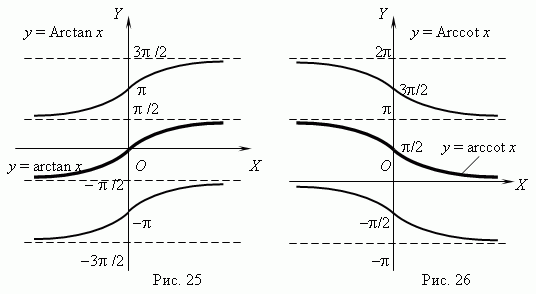
5) y = arcsin x, arccos x, arctg x, arcctg x
6) y = ex

28. Предел числовой последовательности. Бесконечно большие и бесконечно малые числовые последовательности. Свойства бесконечно малых.
Число а называется пределом числовой последовательности xn, если любой E-определенности > 0 существует N, меньшее любой n => |xn-a|< E-определённости, т.е. xn принадлежит E -определенности.
Последовательность
{αn}
называется бесконечно малой, если
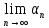 = 0
= 0
Последовательность
{xn}
называется бесконечно большой, если {
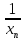 } – бесконечно малая
} – бесконечно малая
Свойства бесконечно малых:
1) αn
+
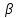 n
– бесконечно
малая
n
– бесконечно
малая
2) αn
*
 n
– бесконечно малая
n
– бесконечно малая
3) αn * с – бесконечно малая, c – действительное число
4) αn
*
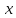 n
– бесконечно
малая, xn
– ограниченная
n
– бесконечно
малая, xn
– ограниченная
29. Основные теоремы о пределах последовательностей.
1) Если предел последовательности существует, то он единственный
2) Сходящаяся последовательность ограничена.
Следствие: Если последовательность не ограничена, то она расходящаяся.
3) A=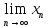 <=> xn
= A
+ αn
, где αn
- бесконечно малая.
<=> xn
= A
+ αn
, где αn
- бесконечно малая.
4) Теорема о
милиционерах: Пусть существует
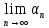 =a.
Существует
=a.
Существует
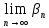 =a
=a
αn
<= xn
<=
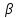 n,
любое n.
n,
любое n.
Тогда
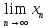 =a
=a
30. Первый и второй замечательные пределы. Число е.
Первый
замечательный предел: αn
– бесконечно
малая, то
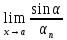 = 1
= 1
Второй замечательный
предел:
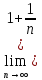 )n
= e
)n
= e
Число
«e» (2,718...) —иррациональное.
Вычисляется с помощью следующего ряда:![]()
Число
e
есть предел выражения
![]()
31. Предел функции. Основные теоремы о пределах функций.
Число A называется пределом функции f(x) в точке x = a (или при x -> a), если всякая окрестность > 0
A
=
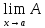
Теоремы:
1) Предел постоянной равен самой постоянной
2)
Постоянный
множитель можно выносить за знак предела:
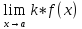 =
k
*
=
k
*
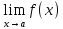
3)
Предел
суммы (разности) функций равен сумме
(разности) пределов этих функций:
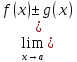 =
=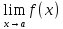 ±
±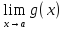
4) Предел произведения функций равен произведению пределов этих функций:
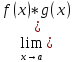 =
=
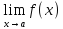 *
*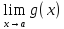
5)
Предел
отношения двух функций равен отношению
пределов этих функций, если только
предел делителя не равен нулю:
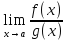 =
=
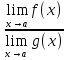 ,
,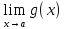 ≠
0
≠
0
32. Замечательные пределы для функций.
1)
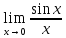 = 1
= 1
Доказательство:
Из доказательства замечательного
предела для последовательности имеем
1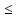
 ≤cos
αn
≤cos
αn
1
≥
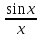 ≥cos
x
≥cos
x
По теореме о
милиционерах в силу
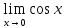 = 1 получаем
= 1 получаем
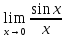 = 1
= 1
2)
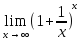 =e
=e
Доказательство: n = [x] – целая часть x. Рассмотрим случай x --> +∞, x > 0
n
≤ x
< n
+ 1 => 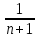 <
<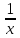 ≤
≤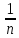 => 1
+
=> 1
+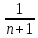 < 1 +
< 1 +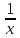 ≤ 1 +
≤ 1 +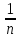
Возводим в степень n ≤ x < n + 1
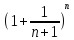 <
(1 +
<
(1 +
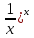 ≤
≤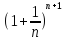
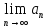 =
=
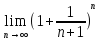 =
=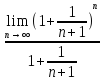
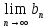 =
=
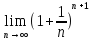 =
=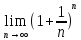 (1
+
(1
+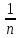 )
= e * 1 = e
)
= e * 1 = e
по теореме о милиционерах:
 =
e
=
e
Рассмотрим случай x --> -∞
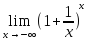 =
[t
= -x]
=
=
[t
= -x]
=
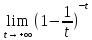 =
=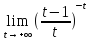 =
= =
=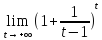 =
=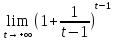 *
*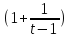 =e*1
= e
=e*1
= e
33. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
Сравнение бесконечно малых:
1.
Если
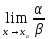 = А (А – действительное число0), то α и ß называются бесконечно малыми
одного порядка.
= А (А – действительное число0), то α и ß называются бесконечно малыми
одного порядка.
2.
Если
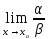 = 0, то α называется бесконечно малой
более высокого порядка , чем ß.
= 0, то α называется бесконечно малой
более высокого порядка , чем ß.
3.
Если
 = ∞, то α называется бесконечно малой
более низкого порядка, чем ß.
= ∞, то α называется бесконечно малой
более низкого порядка, чем ß.
4.
Если
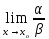 не
существует, то α и ß называются несравнимыми
бесконечно малыми.
не
существует, то α и ß называются несравнимыми
бесконечно малыми.
Функция
f(x)
называется бесконечно малой при x
--> a,
если
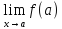 = 0.
= 0.
Если  = 1, то α и ß называются эквивалентными
бесконечно малыми (α ~ ß)
= 1, то α и ß называются эквивалентными
бесконечно малыми (α ~ ß)
Теорема: Сумма бесконечно малых эквивалентна бесконечно малой более низкого порядка из этой суммы.
Таблица эквивалентных бесконечно малых:
sin x ~ х
tg x ~ х
arcsin х ~ х
arctg x ~ х
1 - cos x ~ x2/2
ех – 1 ~ х
αх – 1 ~ х*ln(a)
ln(1+х) ~ х
loga(l+х) ~ х•logaе
(1+х)k – 1 ~ k*х, k > 0
