3.3. Решение задачи интерполяции (полиномы первой и второй степени) с использованием полинома Лагранжа

Решим задачу интерполяции с использованием полинома Лагранжа (кусочно-линейная для каждой последовательной пары точек 1+2, 2+3, 3+4, 4+5), кусочно –параболическая интерполяция для каждой последовательной тройки чисел 1+2+3, 3+4+5), результат оформим графически на миллиметровой бумаге;

При – линейная интерполяция

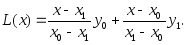
Преобразуем полином Лагранжа для случая 2-х точек.

В первой скобке есть коэффициент а прямой y=ax+b, последних 2 слагаемых есть коэффициентbпрямой

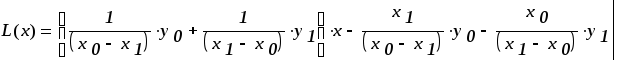
Применим последнюю формулу применительно к нашим точкам в Excel.

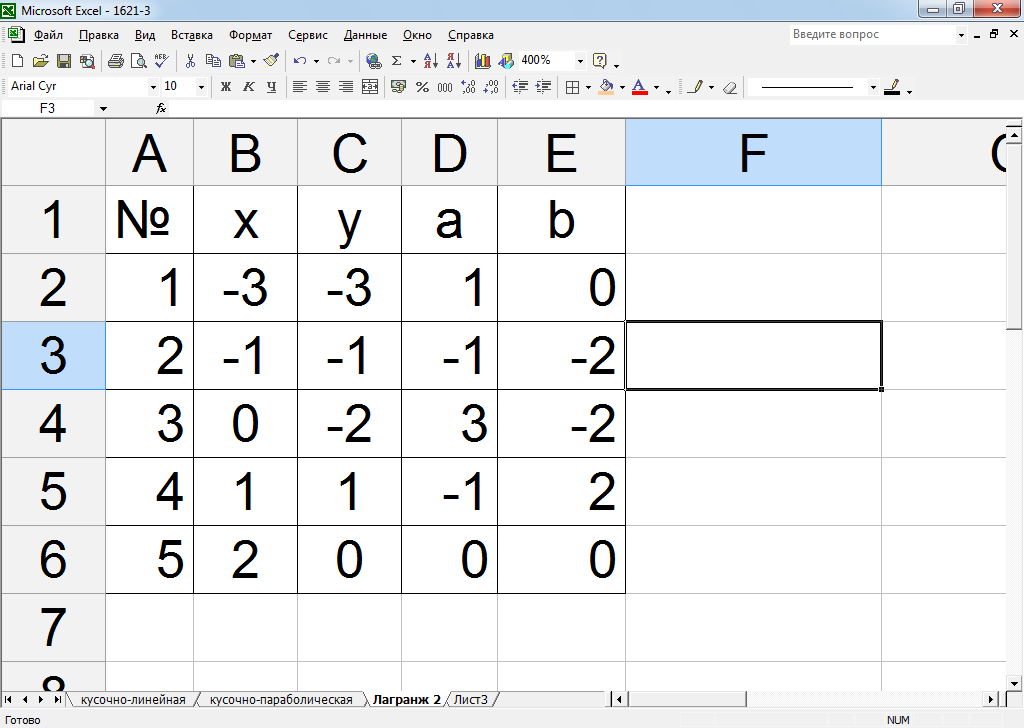
Рисунок 27 – Значения коэффициентов а и bкоэффициентов прямых, соединяющих точки с помощью полинома Лагранжа

Как видим, коэффициенты прямых, получились абсолютно такими же, как и в случае неопределенных коэффициентов.

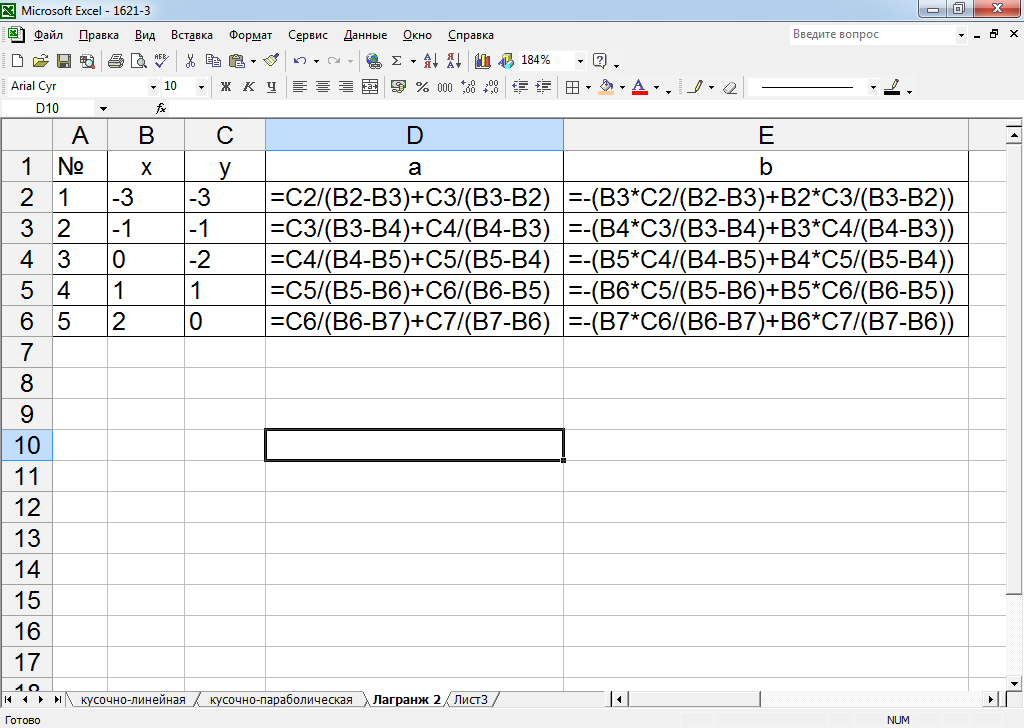
Рисунок 28 – Расчетные формулы нахождения коэффициентов а и bпрямых, соединяющих точки с помощью полинома Лагранжа

Поэтому кусочно-линейная функция полинома Лагранжа будет абсолютно одинакова с той функцией, которую получили методом неопределенных коэффициентов и график интерполяционного полинома Лагранжа 1-й степени совпадет с графиком функции, изображенной на рисунке 22.

При - квадратичная интерполяция

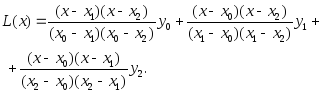
Сгруппируем слагаемые при х²:

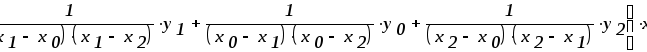
Сгруппируем слагаемые при х:

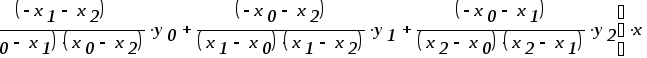
Сгруппируем слагаемые при х⁰:

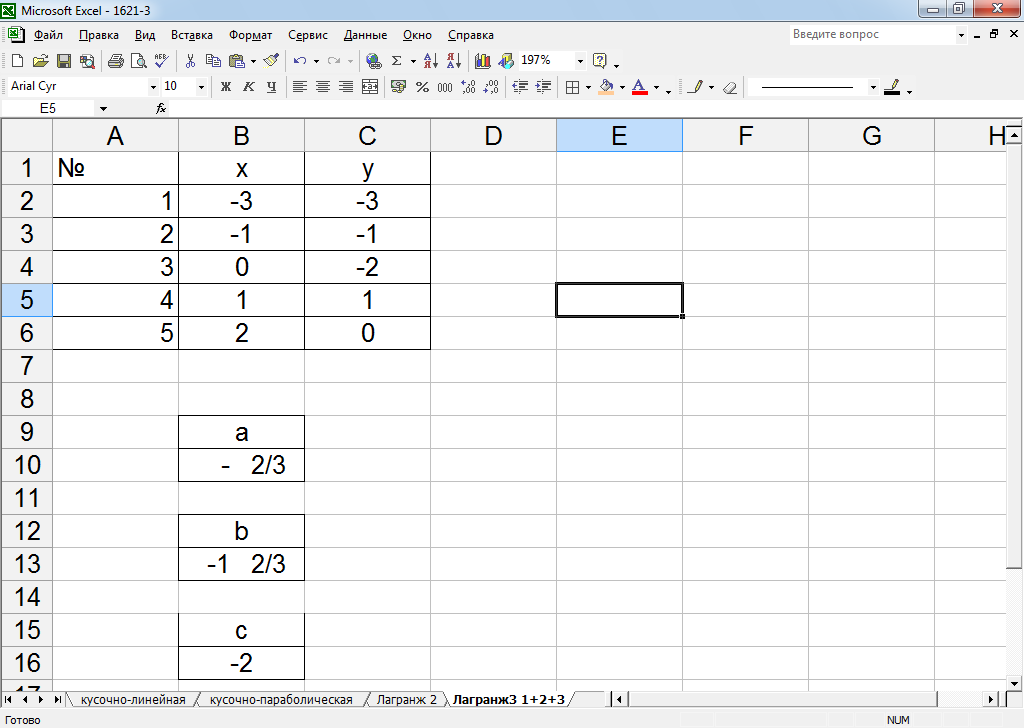
Рисунок 29 – вывод коэффициентов параболы через интерполяционный полином Лагранжа 2-й степени

Для того, чтобы записать эти громоздкие формулы и не запутаться, вновь применим метод именованных ячеек и присвоим ячейкам с координатами точек имена х0,у0, х1,у1, х2, у2 (русскоязычные названия). При вводе формулы просто печатаем эти адреса:

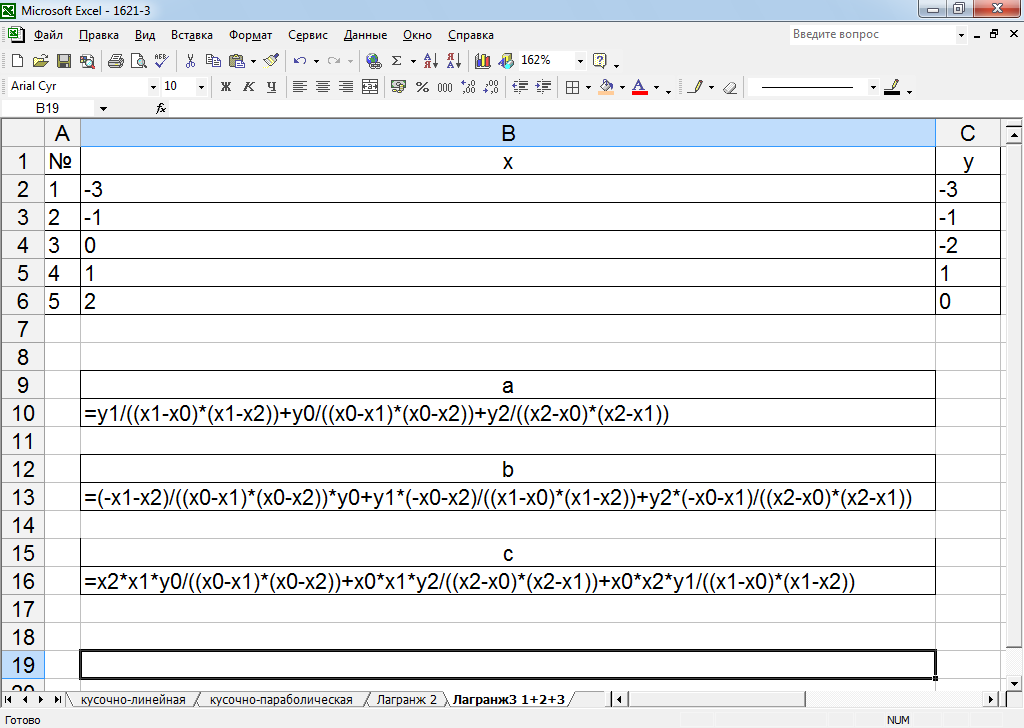
Рисунок 30 -- Формулы расчета

Чтобы рассчитать коэффициенты параболы через интерполяционный полином Лагранжа, перебьем значения в именованных ячейках на координаты 3-ей, 4-ой и 5-ой точек.

Как видим, все значения интерполяционных парабол совпадают с методом неопределенных коэффициентов, и поэтому график кусочно-параболической функции совпадет с графиком, изображенным на рисунке 26.

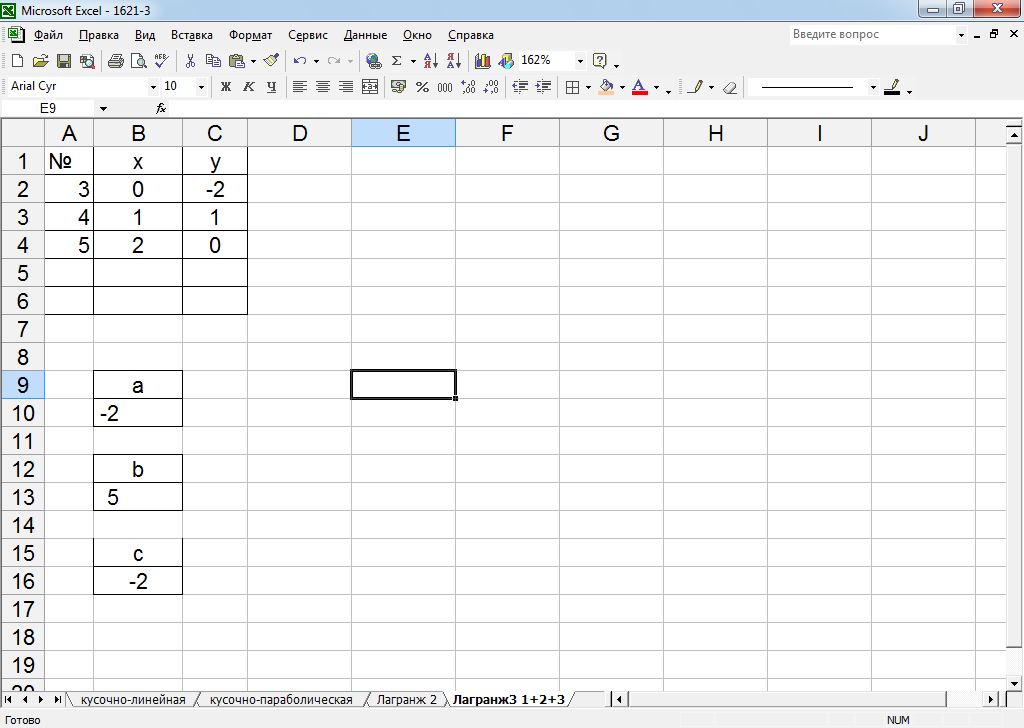
Рисунок 31 – Вывод коэффициентов параболы через интерполяционный полином Лагранжа 2-й степени

3.4. Решение задачи аппроксимации (полиномы первой и второй степени) методом наименьших квадратов

Решим задачу аппроксимации полиномом 1-й и 2-й степени методом наименьших квадратов для всех точек 1+2+3+4+5, результат оформить графически на миллиметровой бумаге.

1) найдем уравнение линейной регрессии y на в виде, где а и b - коэффициенты линейной регрессии.

Найдем выборочный коэффициент корреляции:

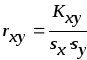
где ,- статистические оценки (среднеквадратические отклонения)

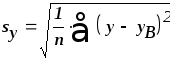
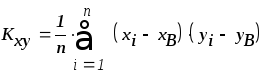
коэффициент корреляции

Здесь ,- средние выборочные, которые находятся по формуле арифметической средней:

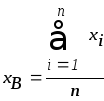
Для облегчения расчетов составим расчетную таблицу и по ней найдем данные по формулам, приведенным выше:

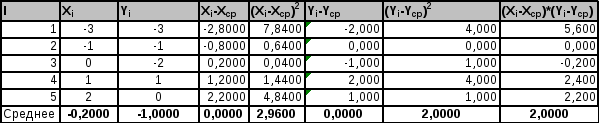
Рисунок 32 -- Расчет значений

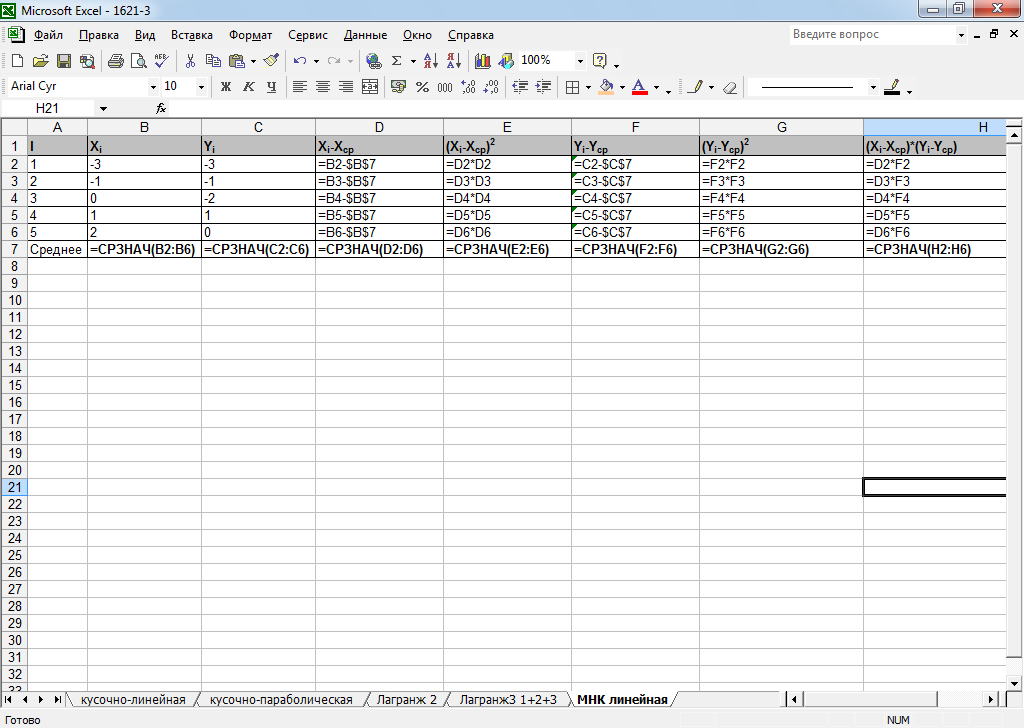
Рисунок 33 – Расчетные формулы

Из таблицы видно, что

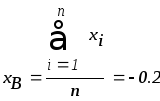
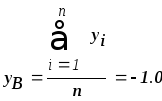
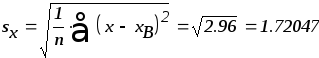
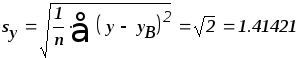
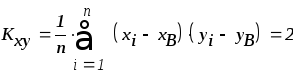
Найдем выборочный коэффициент регрессии по формуле:

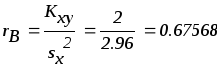
Составим выборочное уравнение регрессии по формуле:

Коэффициент регрессии характеризует изменение оценок по данной совокупности на единицу. C увеличением коэффициентана 1 коэффициент Y увеличивается враза.

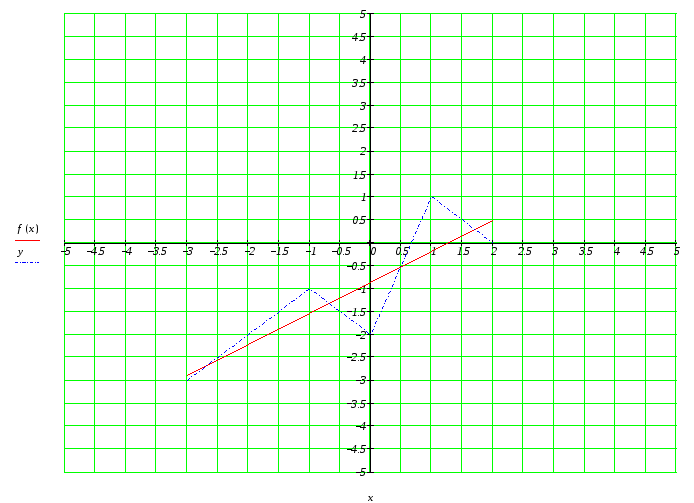
Рисунок 34 – Аппроксимирующая прямая

Если уравнение регрессии представляет собой полином некоторой степени, то при использовании метода наименьших квадратов коэффициенты этого полинома находят решением системы линейных уравнений. Например, требуется определить по методу наименьших квадратов коэффициенты квадратичной функции — параболы второго порядка:

y = b₀ + b₁ x + b₁₁ x²

В этом случае

и система нормальных уравнений имеет вид:

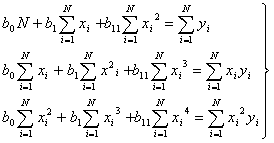
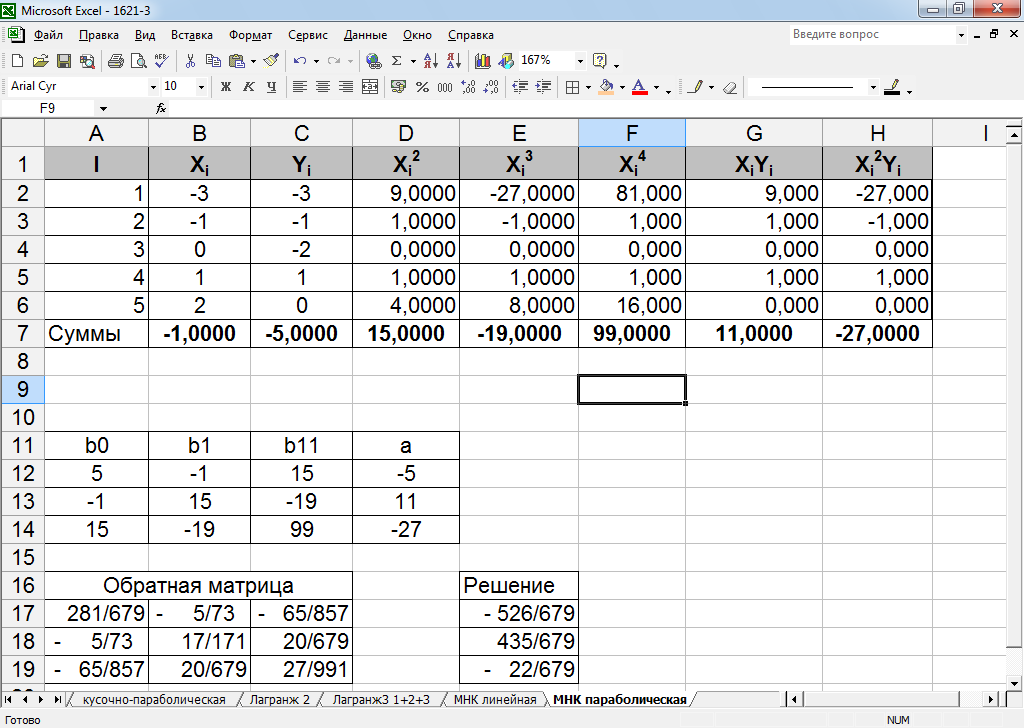
Рисунок 35 -- Нахождение коэффициентов методом обратной матрицы

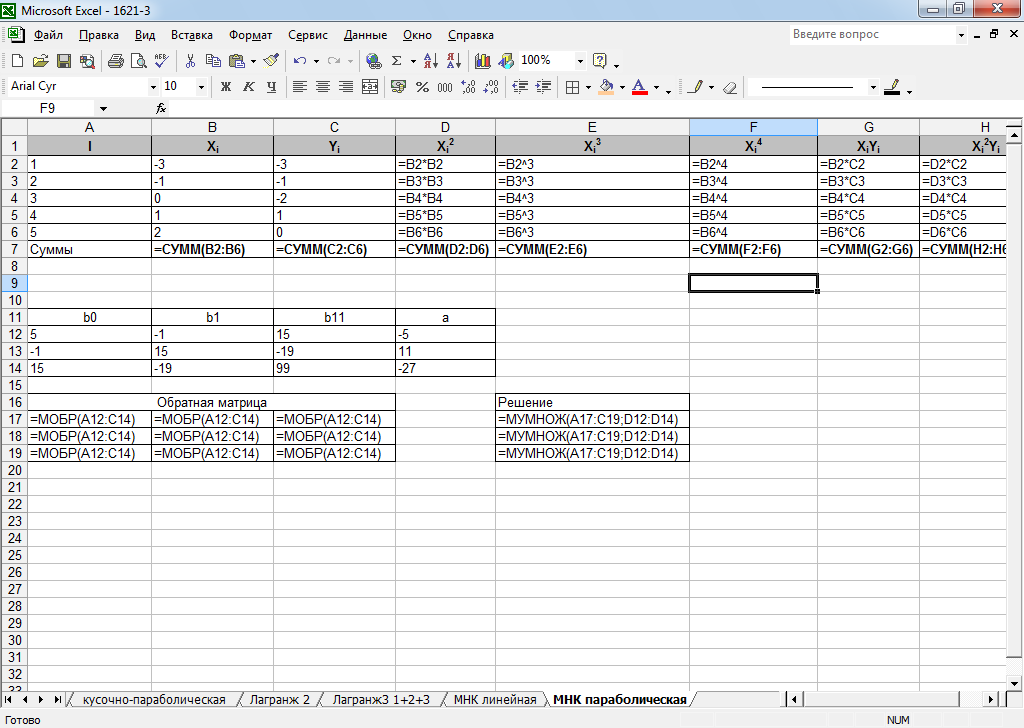
Рисунок 36 - Нахождение коэффициентов методом обратной матрицы (формулы)

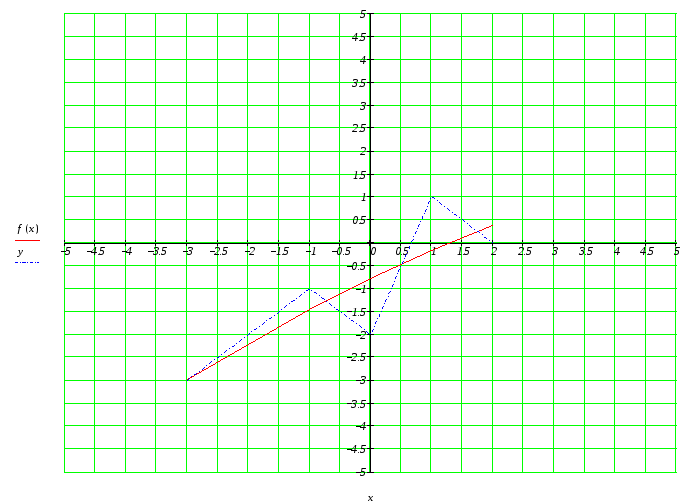
Рисунок 37 – Параболическая аппроксимация.