2.3. Метод простой итерации

Для итерационных методов можно выделить три последовательных этапа:

1. Приведение исходной системы вида 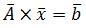к итерационной форме.

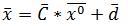2. Проверка условия сходимости.

3. Решение системы одним из методов.

1. Приведем систему к итерационному виду:

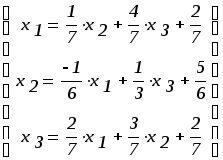
2. В этом виде выполняется условие сходимости:

3. Начнем итерации с нулевого вектора.

На первой итерации х₁, х₂, х₃равны нулю.

На следующих итерациях считаем новые значения переменных по правой части приведенной системы, подставляя значения переменных предыдущего шага.

Рисунок 16 – Реализация метода простой итерации

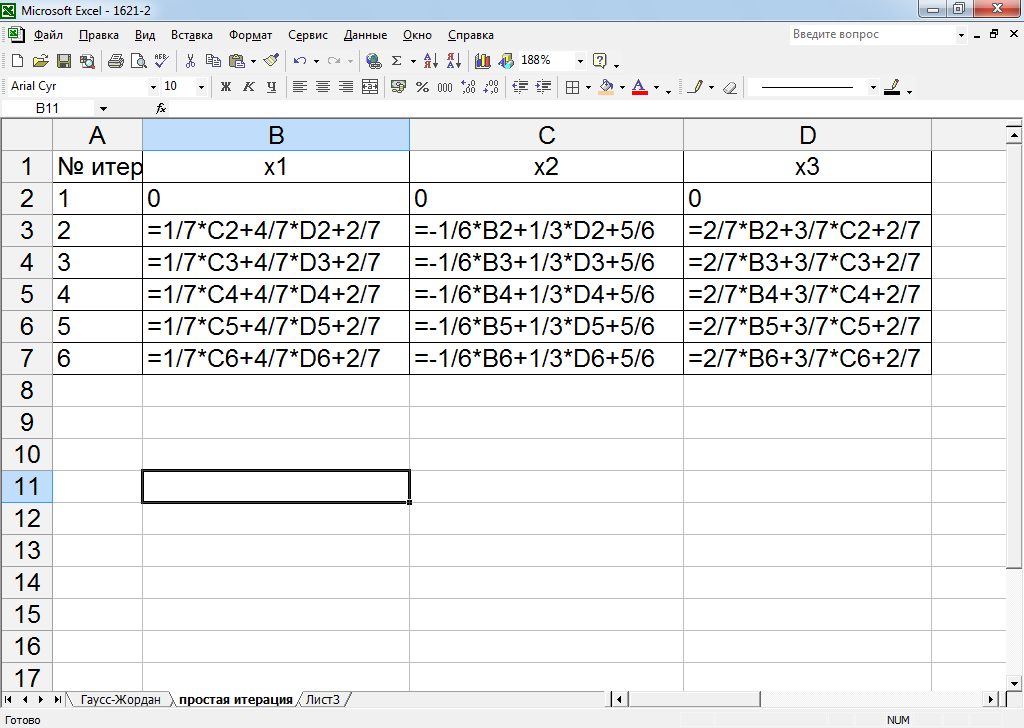
Рисунок 17 – Расчетные формулы к методу простой итерации

Реализовать метод на Excel очень легко. Набрав первые формулы пересчета, скопируем их вниз, и, ради интереса, получим точное решение – вектор (1,1,1). На это потребовалось 6 итераций.

На третьей итерации погрешность метода составила:

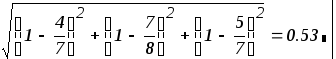
2.4. Метод Зейделя

Метод Зейделя отличается от метода простых итераций только тем, что в пересчет значений основывается на значении х₁, х₂, х₃не предыдущей, а текущей итерации. Потому метод Зейделя сходится быстрее.

Скопируем лист, где проводили метод простых итераций и немного модифицируем его, сделав ссылки на вычисленные значения х в текущей итерации, а не предыдущей.

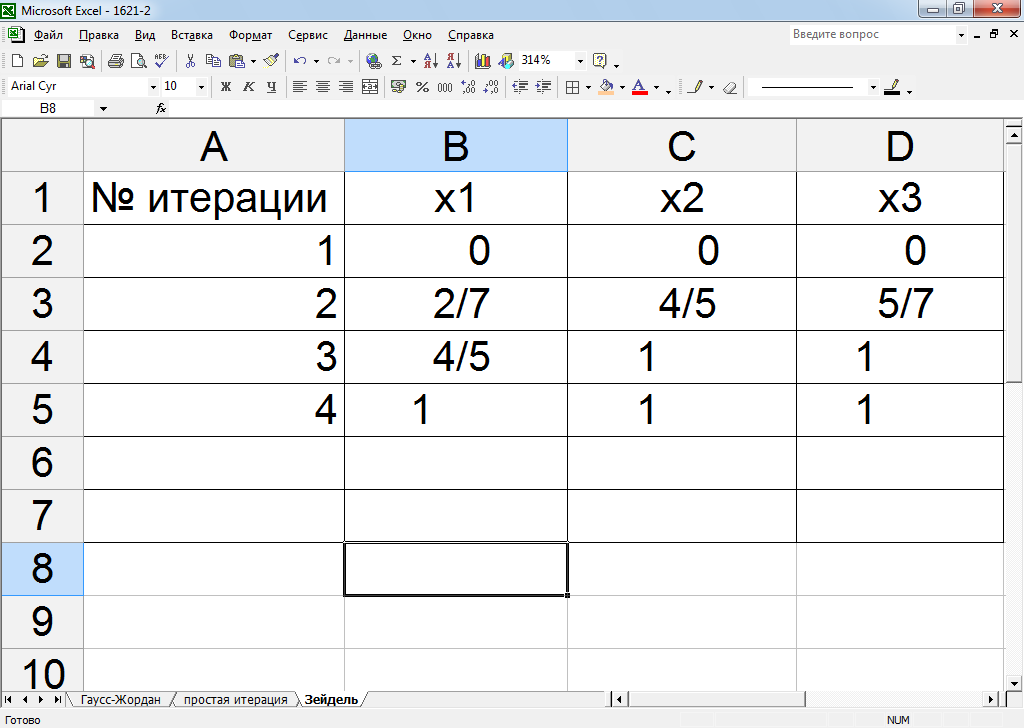
Рисунок 18 – методу Зейделя потребовалось 4 итерации для достижения точного решения

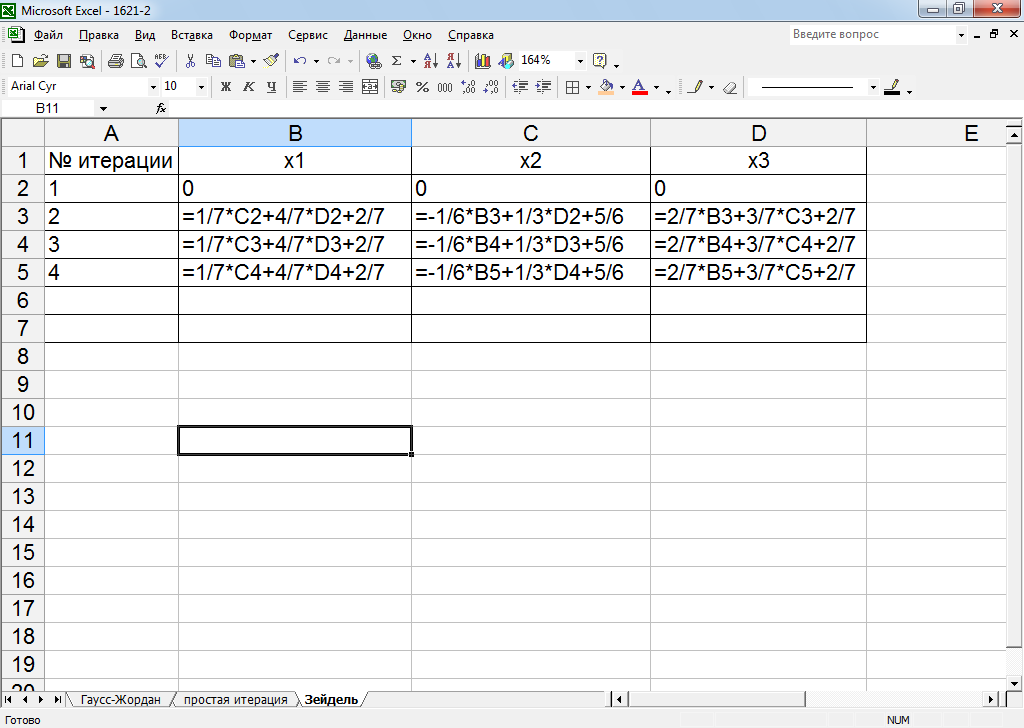
Рисунок 19 –расчетные формулы метода Зейделя

Погрешность метода на 3-ей итерации составила 0,2, что намного меньше погрешности метода простой итерации.

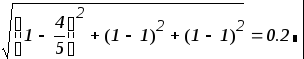
3. Численные методы решения задачи аппроксимации

3.1. Постановка задачи

Многим из тех, кто сталкивается с научными и инженерными расчётами, часто приходится оперировать наборами значений, полученных экспериментальнымпутём или методомслучайной выборки, как правило, эти наборы данных оформляются таблично. Как правило, на основании этих наборов (таблиц) требуется построитьфункцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называетсяаппроксимациейкривой. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных: «…интерполяция— ввычислительной математикеспособ нахождения промежуточныхзначенийвеличины по имеющемусядискретномунабору известных значений…».

В этом разделе дана табличная функция (5 точек). Координаты точек (x_i,y_i) задаются:

x1	x2	x3	x4	x5
-3	-1	0	1	2
y1	y2	y3	y4	y5
-3	-1	-2	1	0

3.2. Решение задачи интерполяции (полиномы первой и второй степени) методом неопределенных коэффициентов

Решим задачу интерполяции методом неопределенных коэффициентов (кусочно-линейная для каждой последовательной пары точек 1+2, 2+3, 3+4, 4+5, кусочно – параболическая интерполяция для каждой последовательной тройки чисел 1+2+3, 3+4+5), результат оформить графически на миллиметровой бумаге;

Пусть табличная функция содержит n точек. В этом случае можно построить различные виды кусочной интерполяции (кусочно-линейная, кусочно-параболическая и т.д.). В случае непрерывной интерполяции, когда используются все точки одновременно, функцию ф(х) будем искать в виде полинома степени n:

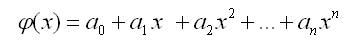
В этом случае степень полинома всегда на единицу меньше числа точек. Действительно, при наличии двух точек мы строили прямую, при наличии трех точек - параболу и т.д. Следовательно, справедливо соотношение n = m — 1.

Для нахождения неизвестных коэффициентов в задачах по математикенеобходимо построить систему линейных уравнений n-го порядка из условия прохождения полинома через все m точек:

В матричном виде система может быть записана следующим образом: С * А = Y где С - квадратная матрица, составленная из известных координат точек; А - вектор неизвестных коэффициентов; Y- вектор-столбец свободных членов.

Для кусочно-линейной интерполяции используем формулу прямой, проходящей через две заданные точки:

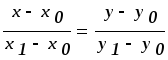
Выражая у из равенства получаем следующий вид прямой:

Иначе говоря, коэффициенты прямой, соединяющей 2 точки рассчитаем по формуле:

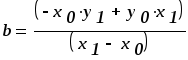
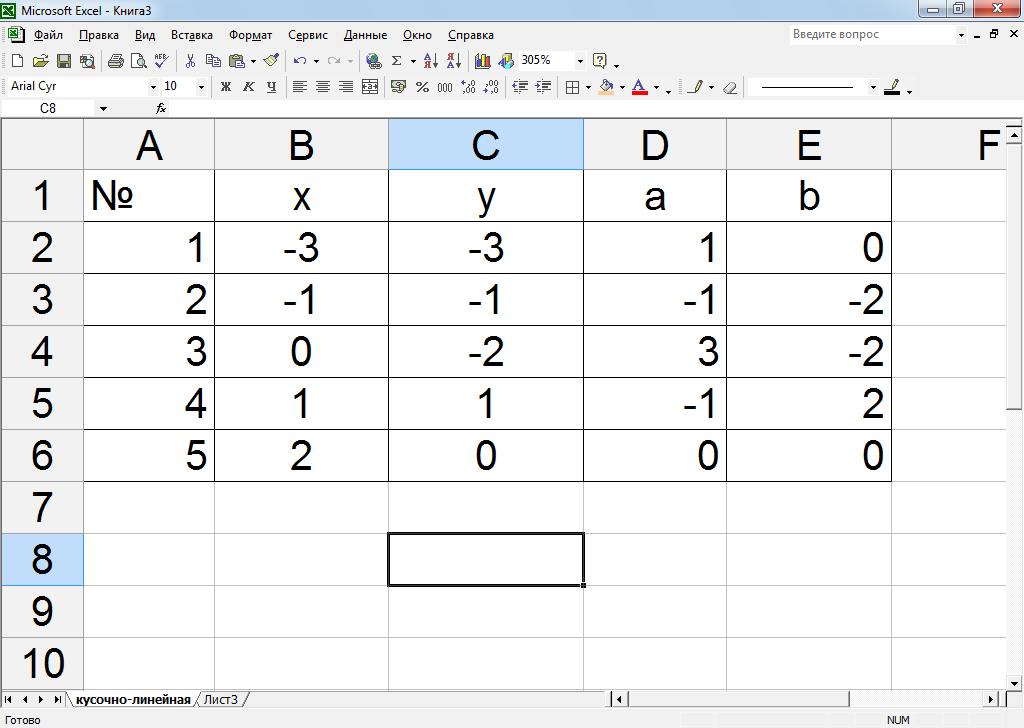
Рисунок 20 – Расчет коэффициентов а и bкоэффициентов прямых, соединяющих точки

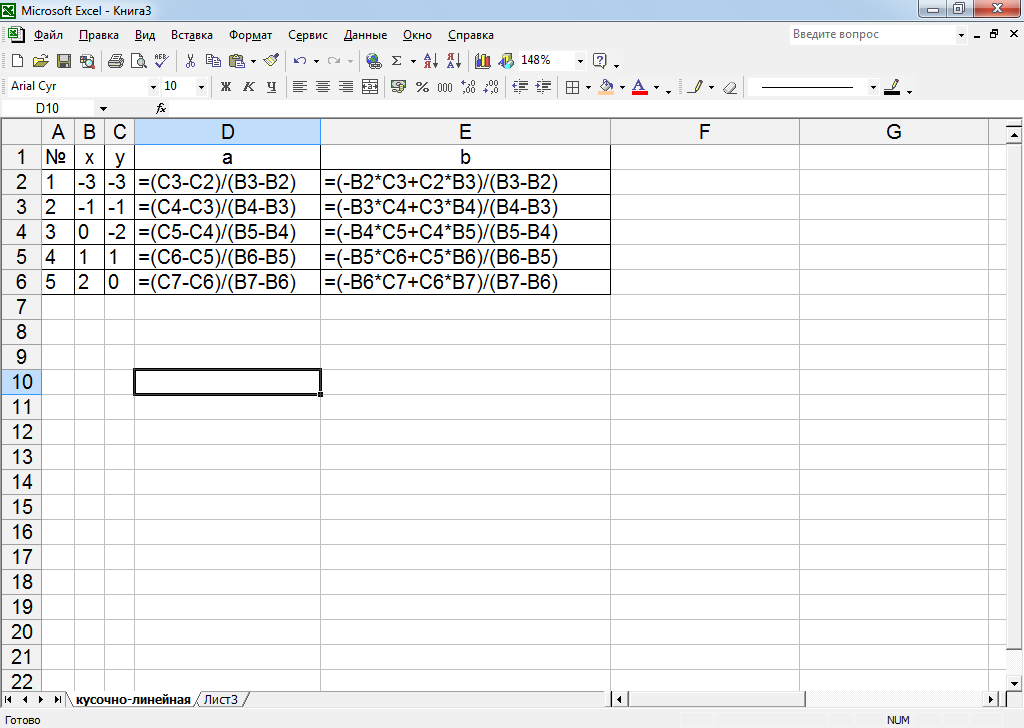
Рисунок 21 – Расчетные формулы кусочно-линейной интерполяции

Таким образом, получаем кусочно-линейную функцию:

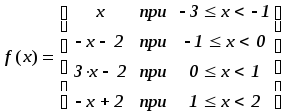
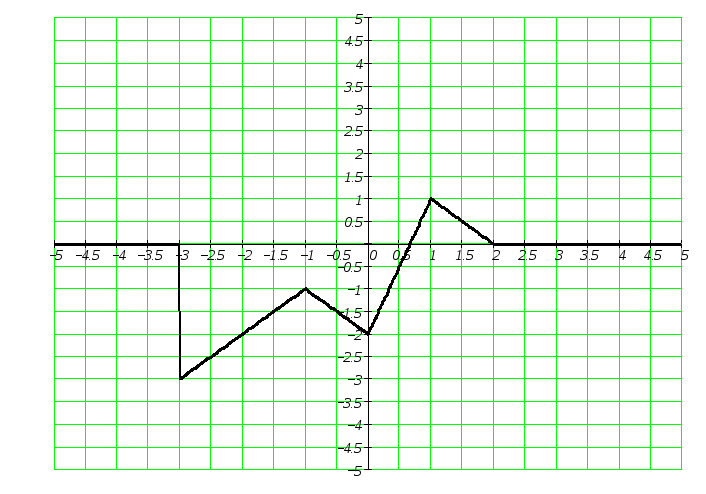
Рисунок 22 – График кусочно-линейной функции проходит строго через заданные точки

При параболической интерполяции необходимо определить значения коэффициентов а, b,cтакой параболы, которая проходит через три заданные точки. Таким образом, необходимо решить СЛАУ относительно а,b,c

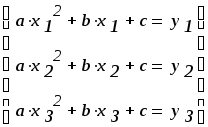
Коэффициентами системы здесь выступают значения х²,х,1. Столбец свободных элементов это столбецу.

В Excel решим эту систему методом обратной матрицы, применяя функции МУМНОЖ, МОБР.

Суть метода:

1. Составляется матрица А^-1, обратная к основной матрице системы А.

2. Обратная матрица умножается на столбец свободных элементов и получаем таким образом столбец – решение.

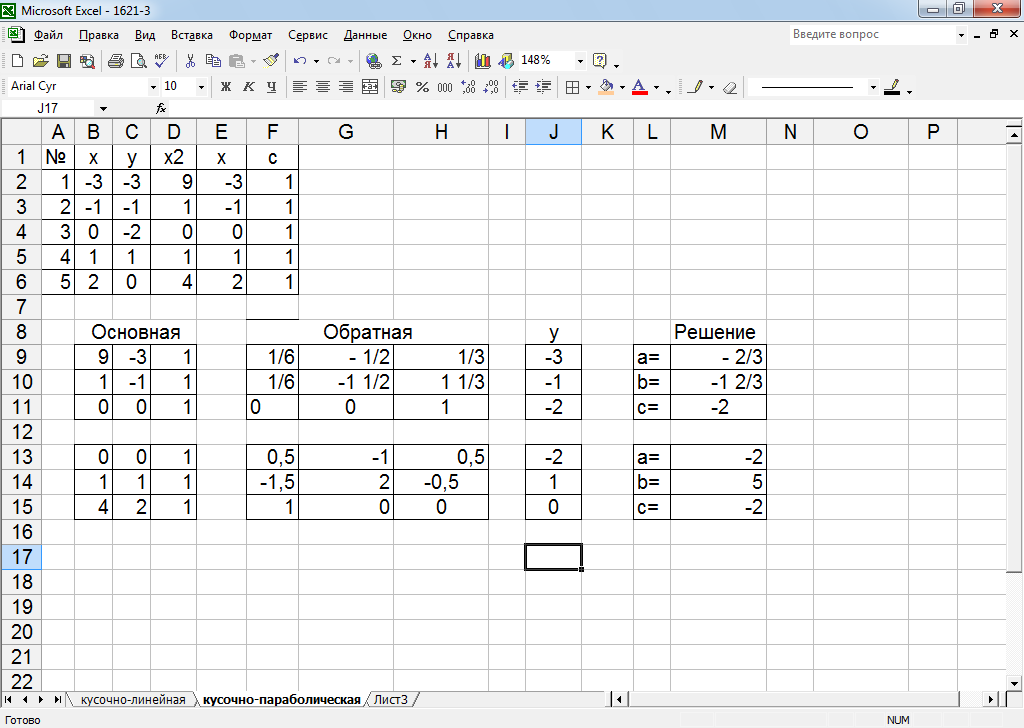
Рисунок 23 – Получение коэффициентов параболы для первой и второй тройки точек.

Получение обратной матрицы в Excel имеет свою специфику:

1. На свободном месте листа выделим область, эквивалентную по размерам с исходной матрицей.

2. Введем формулу “=МОБР(ak;fg)”, где ak – координаты левого верхнего угла, а fg – координаты правого нижнего угла исходной матрицы.

3. Нажмем комбинацию клавиш “Ctrl+Shift+Enter” (если нажмем просто Enter, искомый результат не получим)

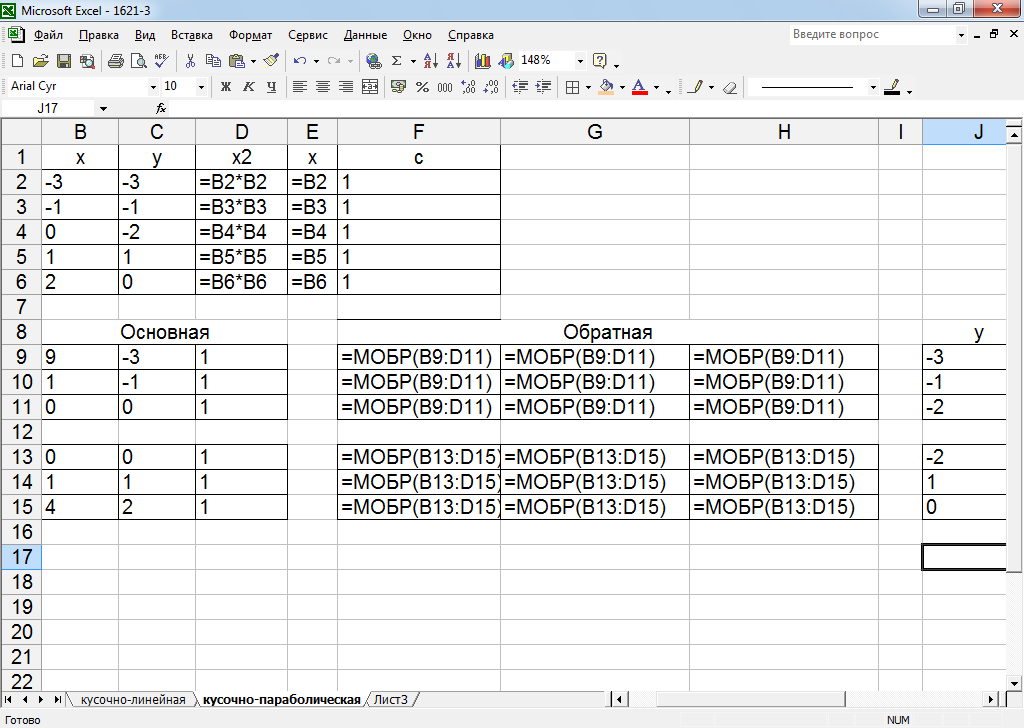
Рисунок 24 – Левая часть листинга для кусочно-параболической интерполяции

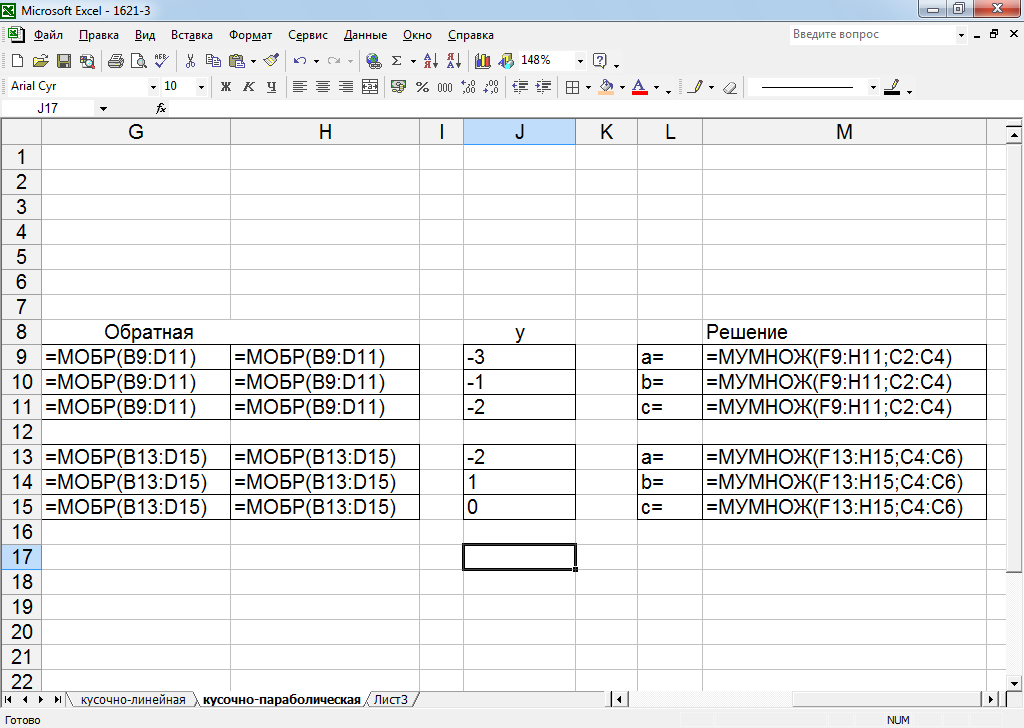
Рисунок 25 – Правая часть листинга для кусочно-параболической интерполяции

Таким образом, кусочно-параболическая функция имеет вид:

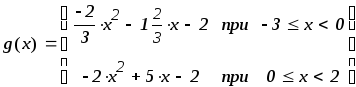
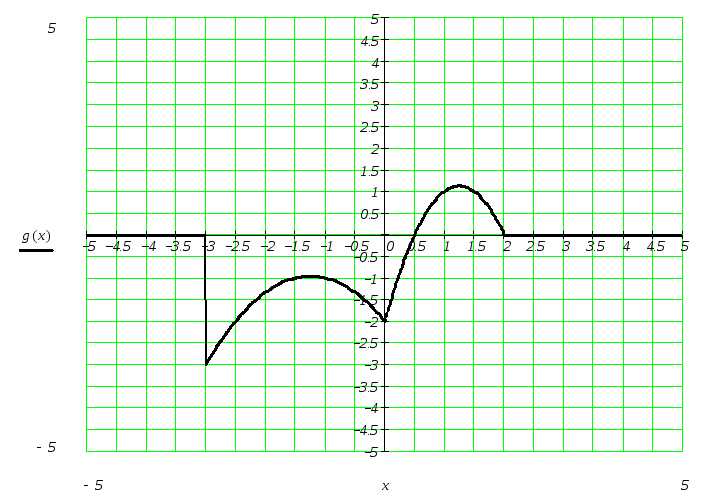
Рисунок 26– График кусочно-параболической функции проходит строго через заданные точки