1.4. Метод Ньютона

Уточним значение корня методом Ньютона с точностью ε=0,001

В литературе этот метод часто называют методом касательных, а также методом линеаризации. Выбираем начальное приближение С₀. Допустим, что отклонение С₀от истинного значения корня С_*мало, тогда, разлагаяf(C_*) в ряд Тейлора в точке С₀, получим

f(C_*) =f(C₀) +f(C₀) (C_*-C₀) +

Если f(C₀)0 , то в (8) можно ограничится линейными поC=C-C₀членами. Учитывая, чтоf(C_*)=0, из (9) можно найти следующее приближение для корня

C₁=C₀ –f(C₀) /f(C₀)

или для (n+1)-го приближения

C_n+1=C_n–f(C_n) /f(C_n)

Для окончания итерационного процесса можно использовать одно из двух условий

C_n+1 –C_n 

или

f(C_n+1).

Исследование сходимости метода Ньютона проводится аналогично предыдущему случаю. Самостоятельно получить, что при выполнении условия

f''(C)/2f'(C)<1.

метод Ньютона имеет квадратичную скорость сходимости ().

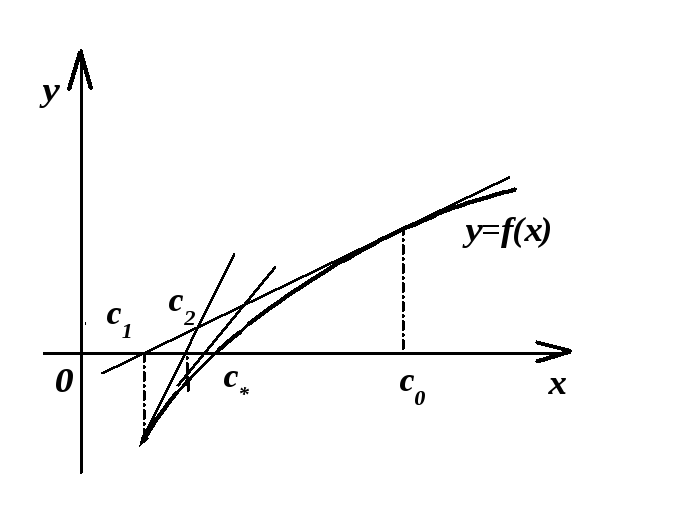
Рисунок 7 -- Графическая интерпретация метода Ньютона для решения уравнения вида f(х)=0.

В нашем случае ,условие f''(C)/2f'(C)<1 не выполняется, поэтому, очевидно, метод будет сходиться медленнее.

Исходным значением для метода простых итераций будет значение х=0,3.

Создадим лист Excel, как показано на рисунке.

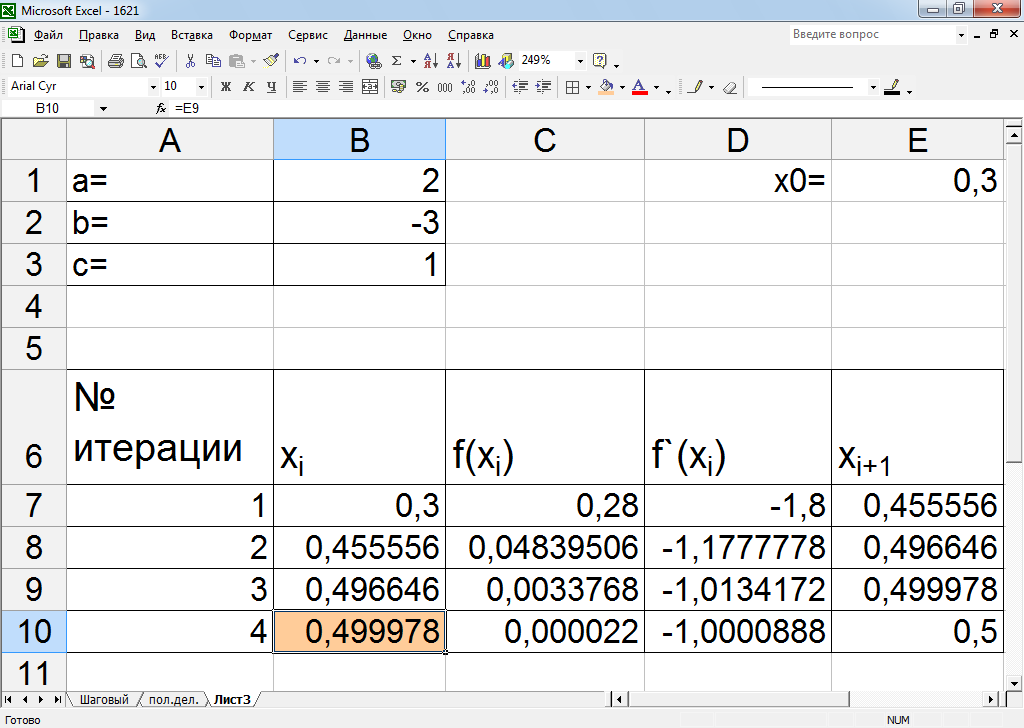
Рисунок 8 – Реализация метода Ньютона (касательных)

Исходные данные вновь имеют собственные номера. Остальные значения рассчитываем, как показано на рисунке 8.

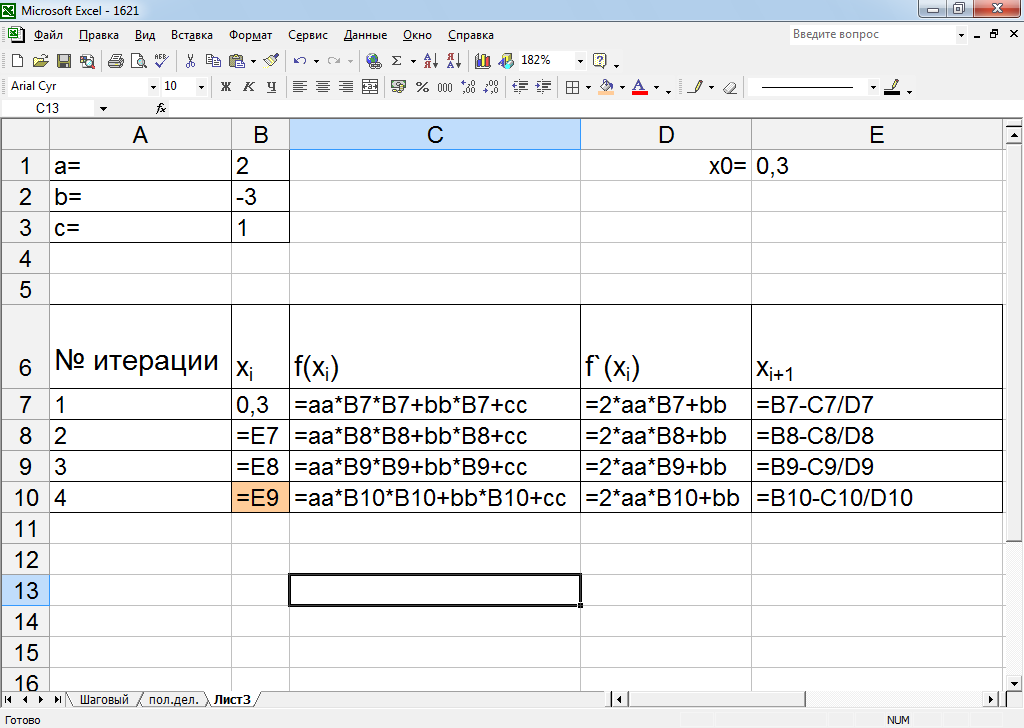
Рисунок 9 – Рабочие формулы метода Ньютона

На шаге 4 видим, что значение функции в точке х=4,99978 равно 0,000022, то есть заданная 0,0001 точность достигнута. Получаем значение корня х=0,499978 методом Ньютона.

1.5. Метод простой итерации

Уточним значение корня методом простой итерации с точностью ε=0,03

При использовании этого метода исходное нелинейное уравнение (1) необходимо переписать в виде

Обозначим корень этого уравнения C_*. Пусть известно начальное приближение корня. Подставляя это значение в правую часть уравнения (2), получаем новое приближение

и т.д. Для (n+1)- шага получим следующее приближение

Таким образом, по формуле (3) получаем последовательность С₀, С₁,…,С_n+1, которая стремиться к корню С_*при n. Итерационный процесс прекращается, если результаты двух последовательных итераций близки, т. е. выполняется условие

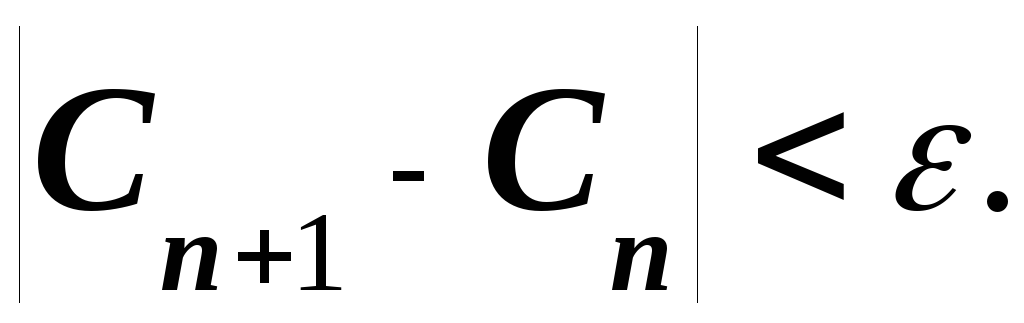
Исследуем условие и скорость сходимости числовой последовательности {C _n} при n. Напомним определение скорости сходимости. Последовательность {C_n}, сходящаяся к пределу С_*, имеет скорость сходимости порядка, если при nвыполняется условие

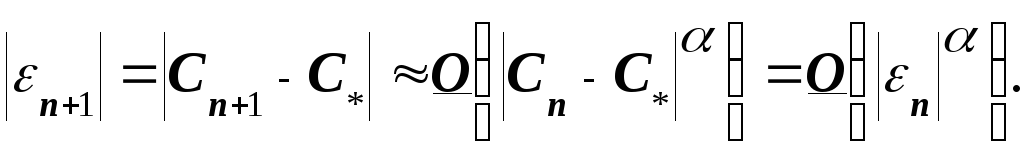
Допустим, что имеет непрерывную производную, тогда погрешность на (n+1)-м итерационном шаге_n+1=C_n+1-C_*=g(C_n)-g(C_*) можно представить в виде ряда

_n+1 C_n+1 –C_*=g(C_*) (C_n-C_*) +g(C_*)_n+

Таким образом, получаем, что при выполнении условия

g(C_*)

Последовательность будет сходиться к корню с линейной скоростью . Условиеg(C_*)является условием сходимости метода простой итерации. Очевидно, что успех метода зависит от того, насколько удачно выбрана функция.

Выразим нашу функцию в виде

Условие сходимости выполняется при х 0,5

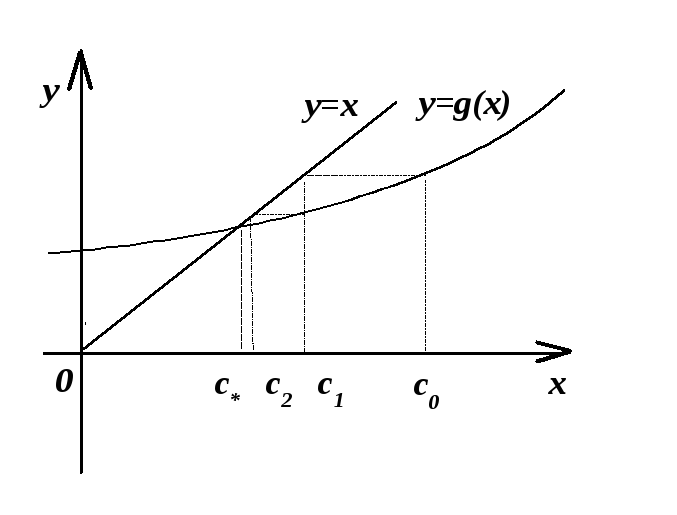
Рисунок 10 -- Графическая интерпретация метода простых итераций для решения уравнения вида x=g(х).

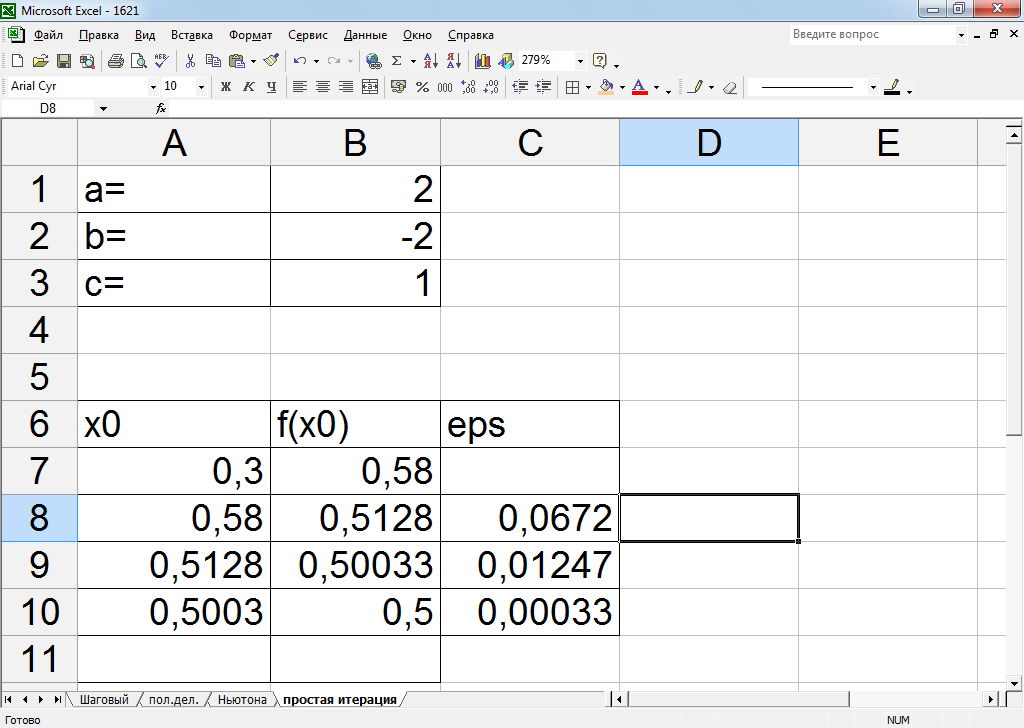
Рисунок 11 – Результат реализации метода простой итерации

На рисунке 12 покажем расчетные формулы при реализации этого метода:

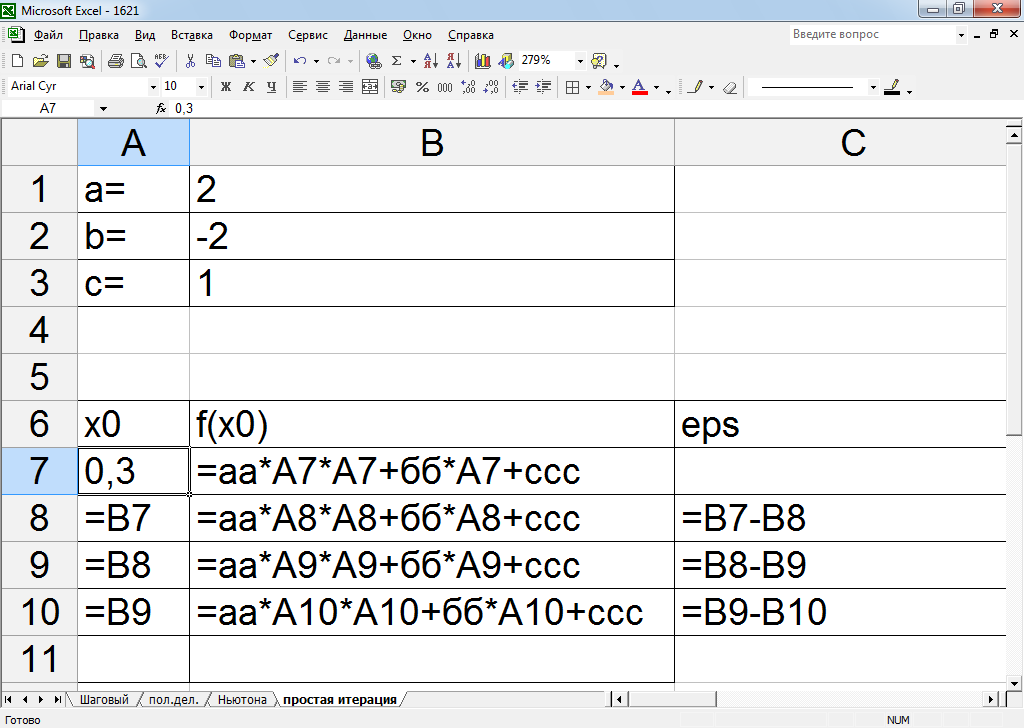
Рисунок 12 – Расчетные формулы реализации метода простой итерации

Корень, найденный методом простой итерации, равен 0,5.