
-
Понятие модуля. Решение простейших уравнений и неравенств с неизвестным под знаком модуля.
Модуль и его свойства.
1. Определение модуля числа:
![]() .
.
2. Геометрически
![]() есть расстояние от точки
есть расстояние от точки
![]() числовой оси до начала отсчета – точки
числовой оси до начала отсчета – точки
![]() .
.
3.
![]() есть
расстояние между точками
есть
расстояние между точками
![]() и
и
![]() числовой оси.
числовой оси.
4. Модуль произведения, частного и степени.
![]() .
.
5.
![]() .
.
Уравнения, содержащие знак модуля.
Уравнения, содержащие знак модуля, можно условно классифицировать по видам, в зависимости от расположения знака модуля. Рассмотрим некоторые виды таких уравнений и методы их решения.
-
Уравнения вида
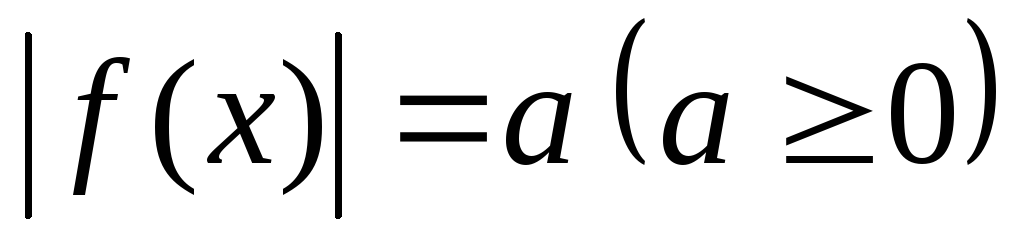 .
Наиболее рациональный путь решения –
переход к совокупности
.
Наиболее рациональный путь решения –
переход к совокупности
![]()
-
Уравнения вида
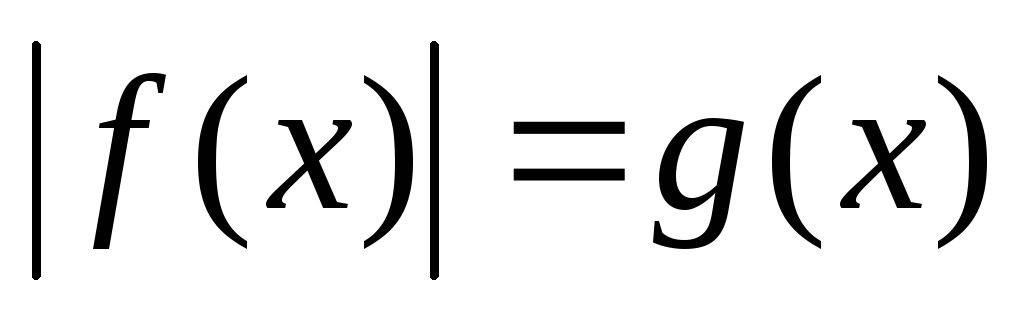 можно двумя способами заменить
равносильными условиями: 1)
можно двумя способами заменить
равносильными условиями: 1)
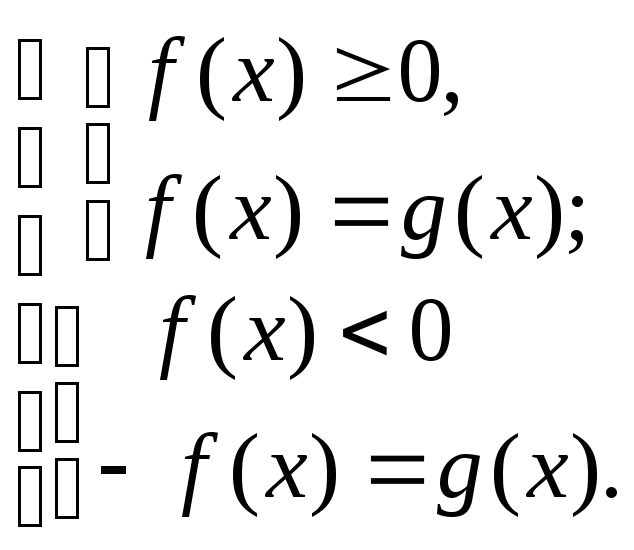
2)

Выбор способа замены зависит от того,
какое из неравенств
![]() или
или
![]() решить легче.
решить легче.
-
Уравнения вида
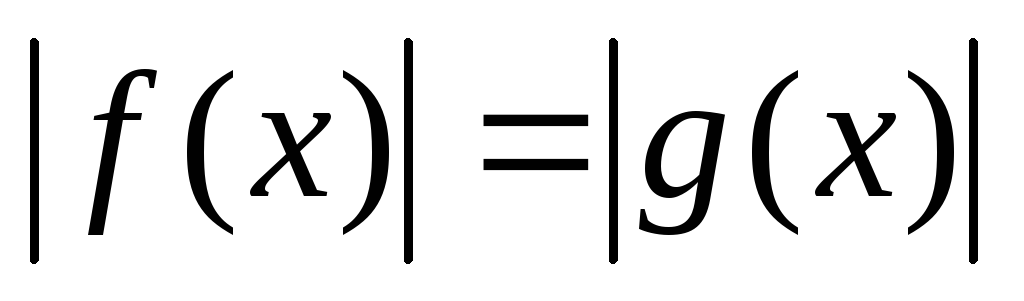 .
Их решение состоит в возведении обеих
частей уравнения в квадрат, так как по
свойству модуля
.
Их решение состоит в возведении обеих
частей уравнения в квадрат, так как по
свойству модуля
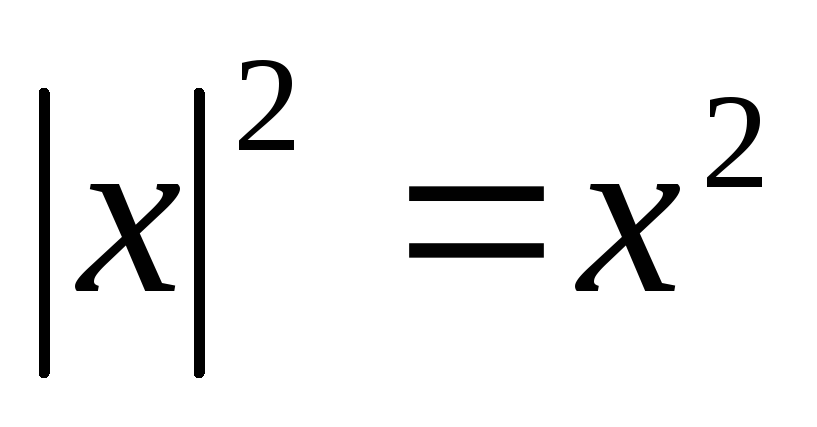 .
Тогда
.
Тогда
![]()
-
Уравнения вида
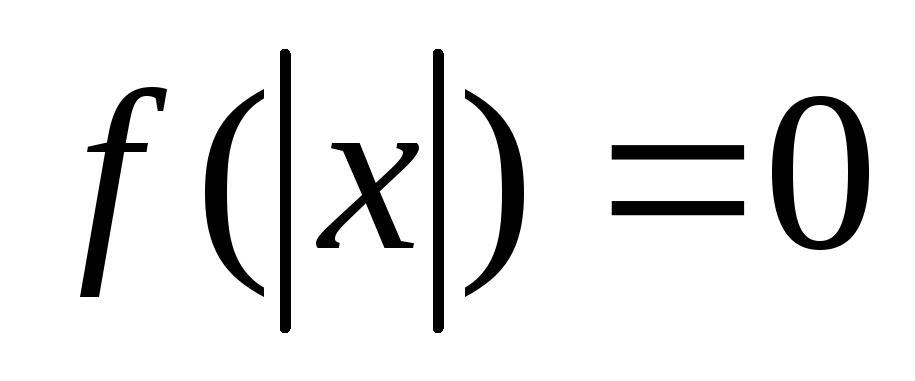 .
Уравнения этого вида можно решать,
используя замену
.
Уравнения этого вида можно решать,
используя замену
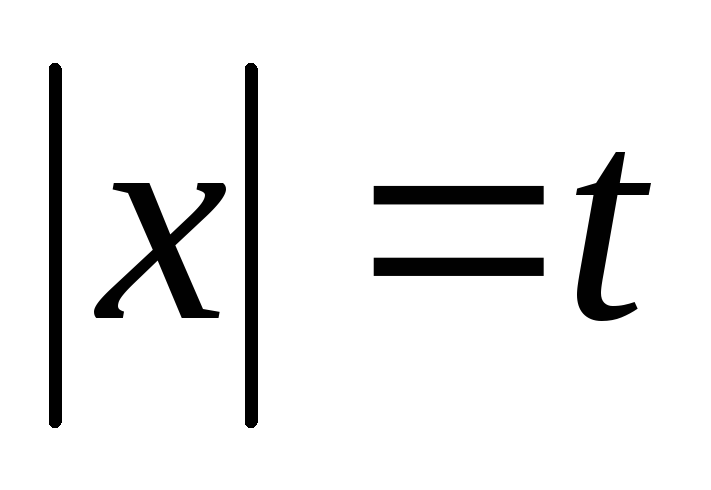 .
.
Пример. Решить уравнение
![]()
Решение: Исходное уравнение равносильно совокупности:
![]()
Решая эти уравнения, получим корни
![]() .
.
Ответ:
![]() .
.
Пример. Решить уравнение
![]()
Решение: Данное уравнение равносильно системе:
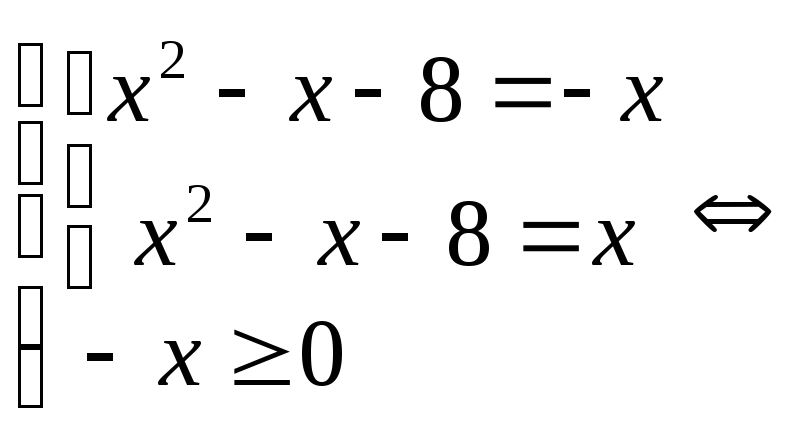
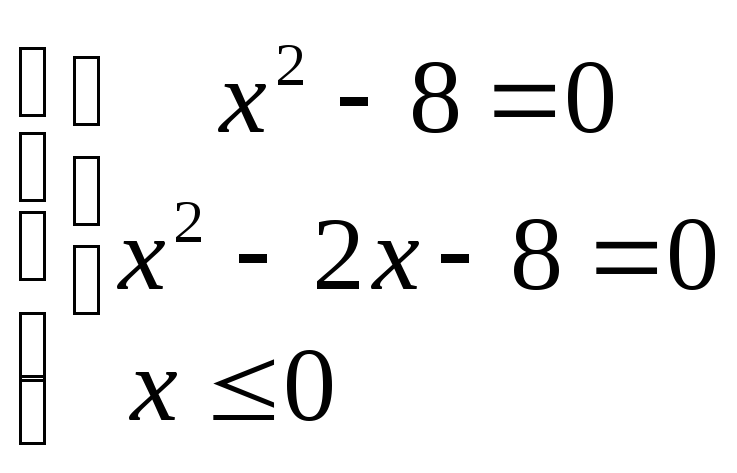 .
.
Решая эти уравнения, получим корни
![]() .
Выберем из них те, которые удовлетворяют
условию
.
Выберем из них те, которые удовлетворяют
условию
![]() .
.
Ответ:
![]() .
.
Пример. Решить уравнение
![]()
Решение: Поскольку в уравнении функция, стоящая под знаком модуля, проще, то лучше записать уравнение, как совокупность двух систем:
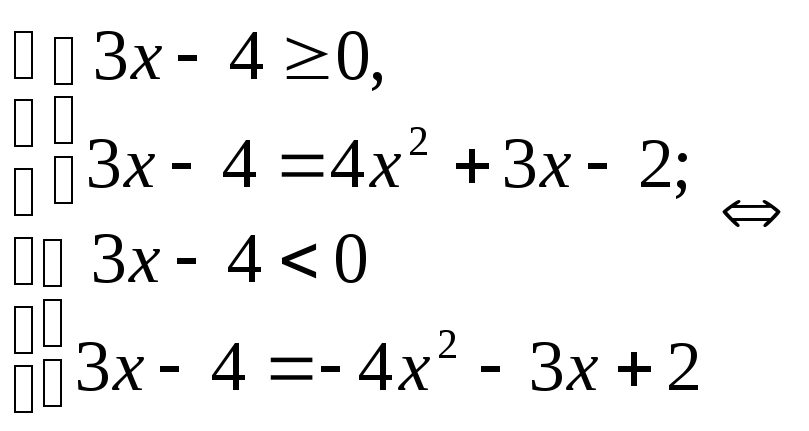
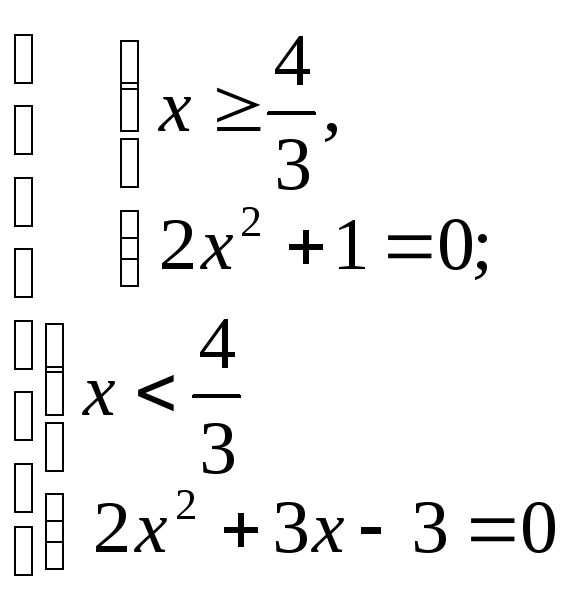 .
.
Уравнение из первой системы совокупности
корней не имеет. Решая уравнение, находим,
что
![]()
Ответ:
![]()
Пример. Решить уравнение
![]()
Решение: Возведем обе части уравнения в квадрат:
![]()
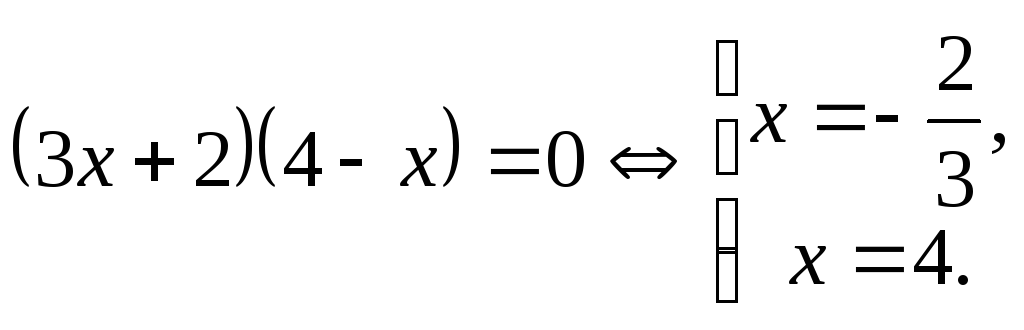
Ответ:
![]()
Пример. Решить уравнение
![]()
Решение: Так как
![]() ,
данное уравнение примет вид:
,
данное уравнение примет вид:
![]()
Сделаем замену:
![]() получим новое уравнение:
получим новое уравнение:
![]() ,
которое имеет два положительных корня
,
которое имеет два положительных корня
![]() .
Значит,
.
Значит,
![]() ,
откуда
,
откуда
![]() .
.
Ответ:
![]()
Дополнительные задачи:
1. Решите уравнение
![]() .
.
Решение:
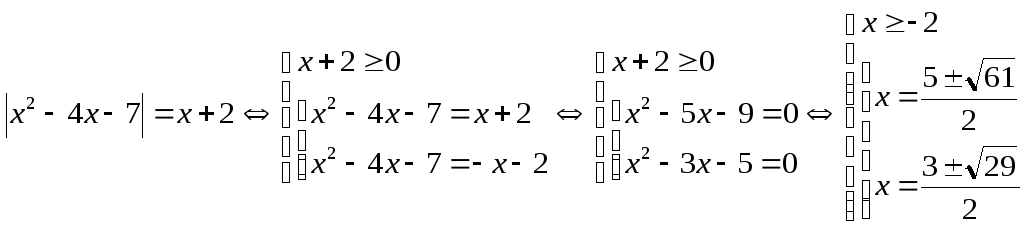 .
.
Ответ:
![]() .
.
2. Найти сумму целых решений
уравнения
![]() .
.
Решение:
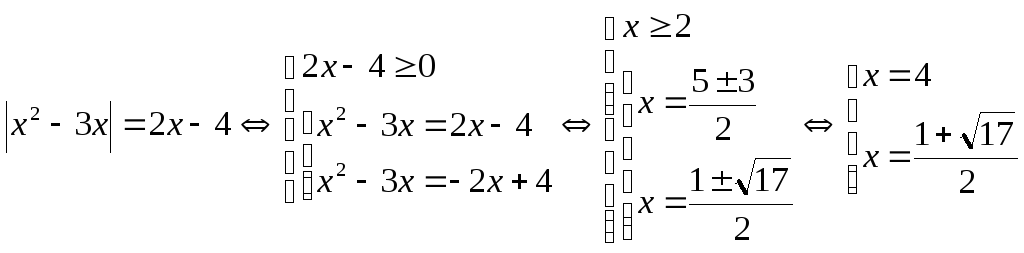 .
.
Целое решение только одно: 4, поэтому сумма решений равна значению единственного целочисленного решения: 4.
Ответ:
![]() .
.
3. Найти сумму всех корней
уравнения
![]() .
.
Решение:
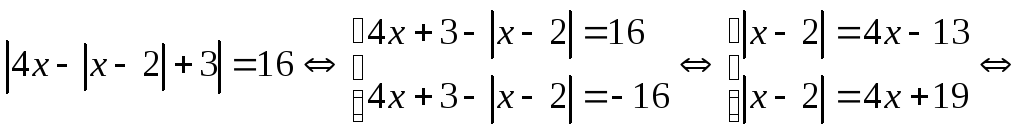
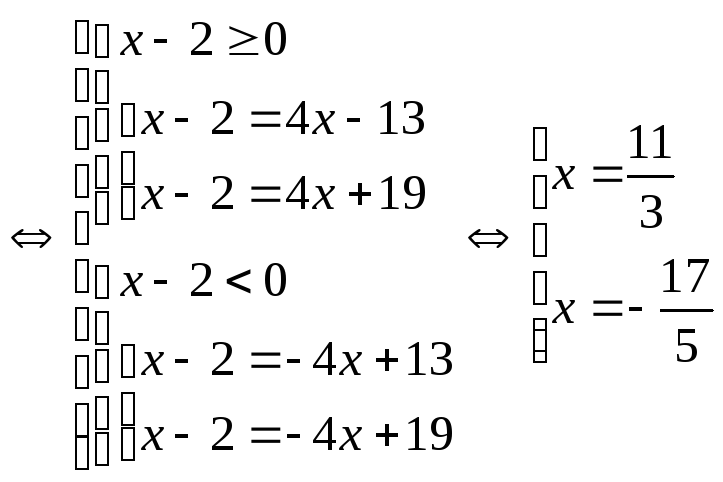
Сумма корней равна
![]() .
.
Ответ:![]() .
.
4. Решите уравнение
![]() .
.
Решение:
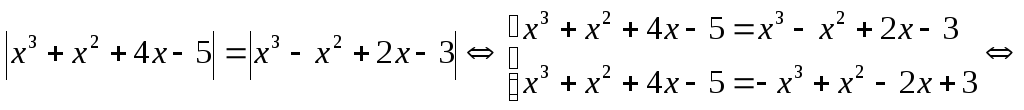
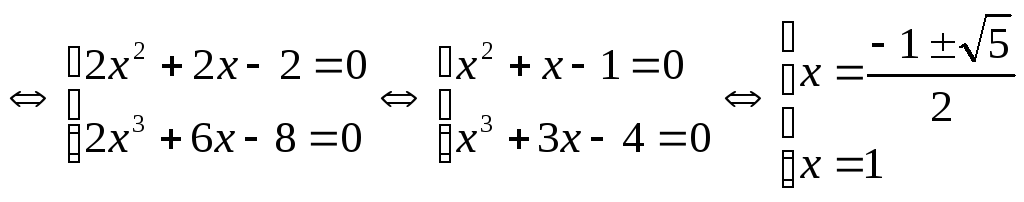 .
.
Ответ:![]() .
.
5. Решите уравнение
![]() .
.
Решение: заметим, что
![]() ,
решим уравнение:
,
решим уравнение:
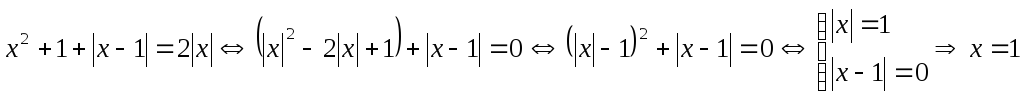 .
.
Ответ:![]() .
.
6. Укажите наибольший корень
уравнения
![]() .
.
Решение: Расставим знаки выражений, стоящих под знаком модуля, на промежутках:
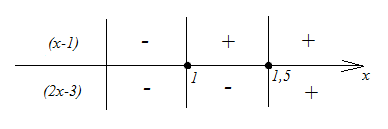
Теперь легко раскрыть модули и получить соответствующие уравнения на промежутках:
1)
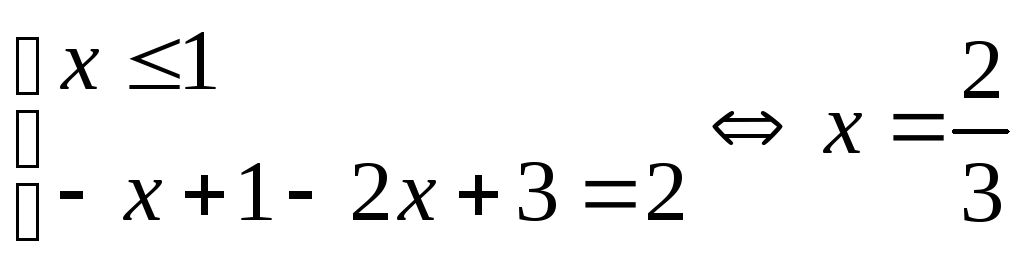 .
.
2)
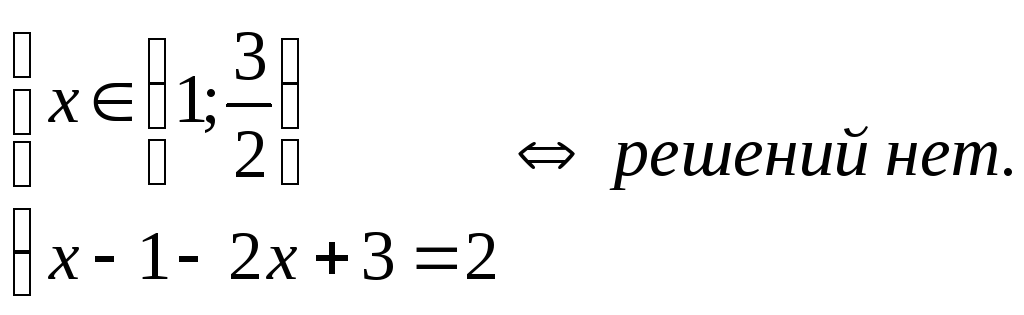
3)
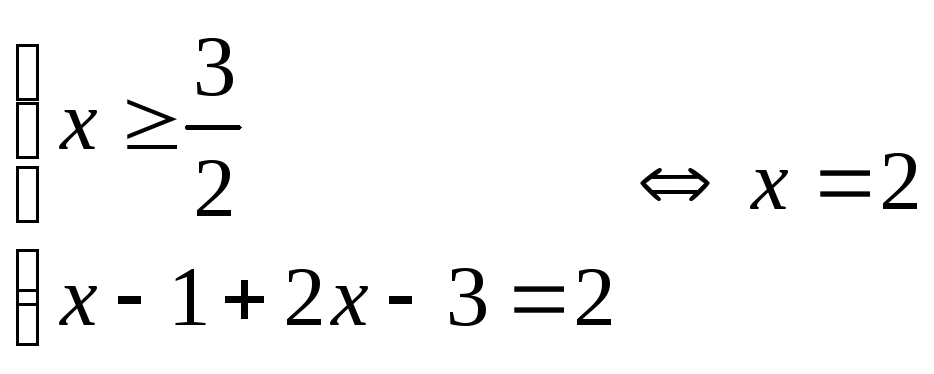 .
.
Отсюда следует, что наибольшим корнем является число 2.
Ответ:![]() .
.
7. Решите уравнение
![]() .
.
Ответ:![]() .
.
Для самостоятельного решения:
Решить уравнения:
|
|
|
|
|
|
|
|
|
|
|
|
Неравенства, содержащие знак модуля.
Перечислим некоторые частные случаи неравенств, содержащих знак модуля, и рассмотрим методы их решения.
-
Неравенство вида
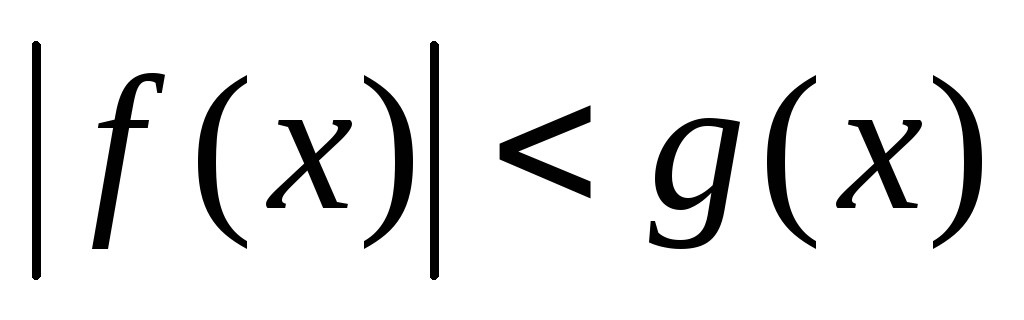 ,
где
,
где
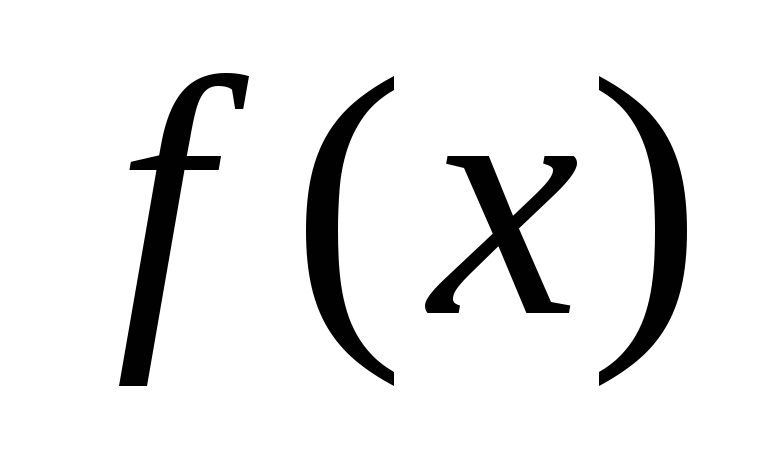 и
и
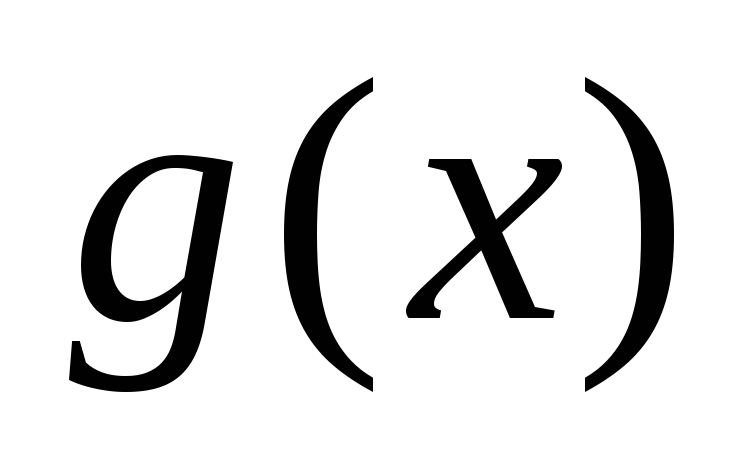 - некоторые функции, равносильно системе
- некоторые функции, равносильно системе
![]()
В частности, неравенство
![]() при любом
при любом
![]() равносильно системе:
равносильно системе:
![]() или
или
![]()
При
![]() неравенство не имеет решений.
неравенство не имеет решений.
-
Неравенство вида
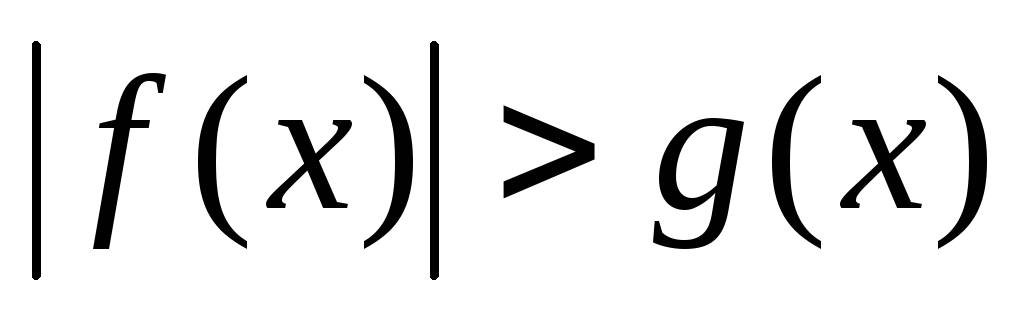 ,
где
,
где
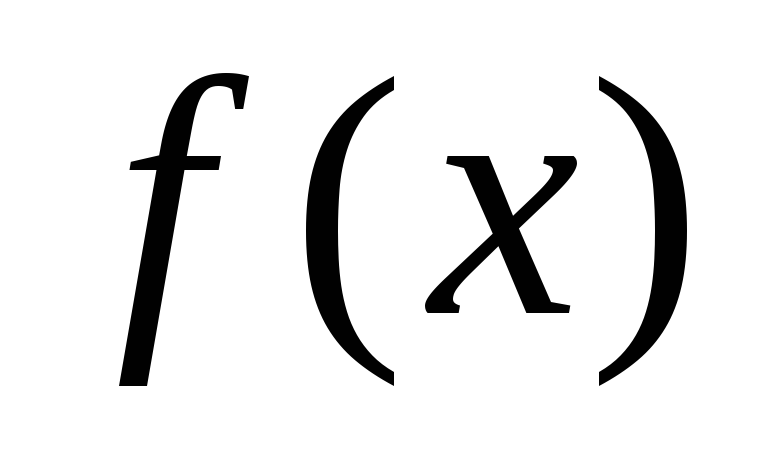 и
и
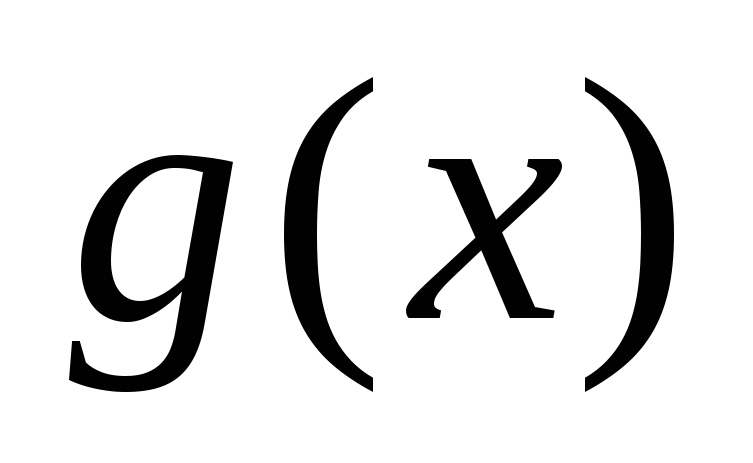 - некоторые функции, равносильно
совокупности:
- некоторые функции, равносильно
совокупности:
![]()
В частности, неравенство
![]() равносильно совокупности:
равносильно совокупности:
![]()
При
![]() неравенство выполняется для всех
неравенство выполняется для всех
![]() при которых функция
при которых функция
![]() имеет смысл.
имеет смысл.
-
Неравенство вида
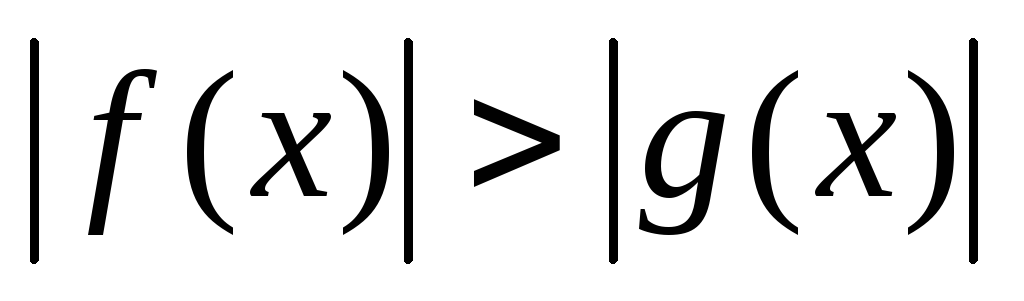 равносильно неравенству
равносильно неравенству
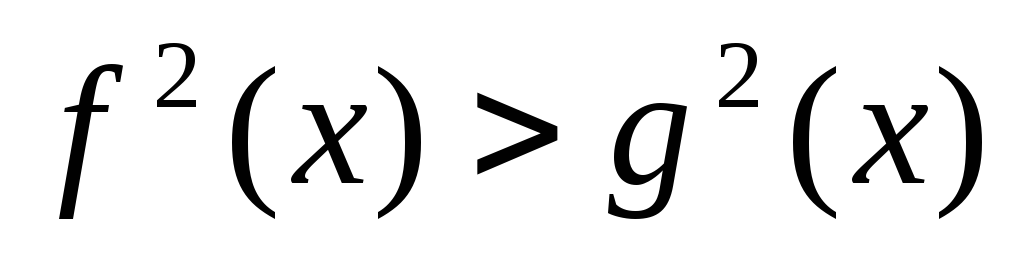 .
Преобразуя последнее неравенство,
получим:
.
Преобразуя последнее неравенство,
получим:
![]()
![]() ,
,
которое решается методом интервалов.
-
Неравенство вида
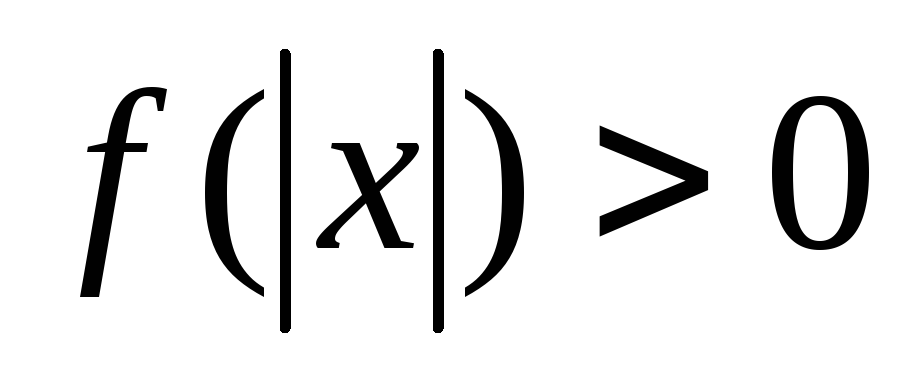 можно решать, используя замену
можно решать, используя замену
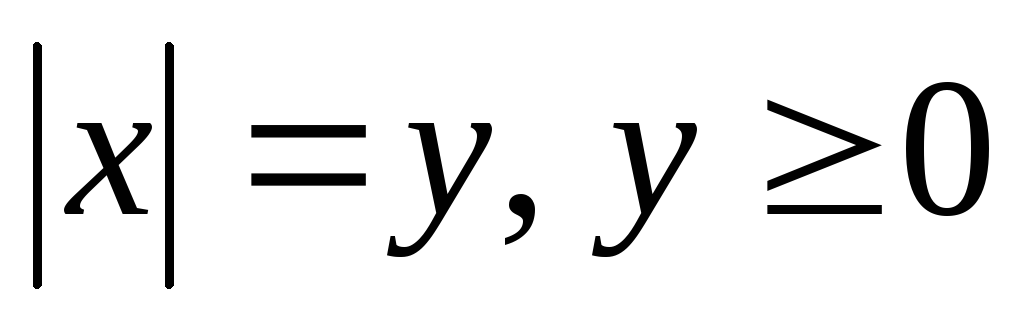 .
.
Пример. Решить неравенство
![]()
Решение: Запишем систему, равносильную исходному неравенству:
![]()
Ответ:
![]() .
.
Пример. Решить неравенство
![]()
Решение: Запишем систему, равносильную исходному неравенству:
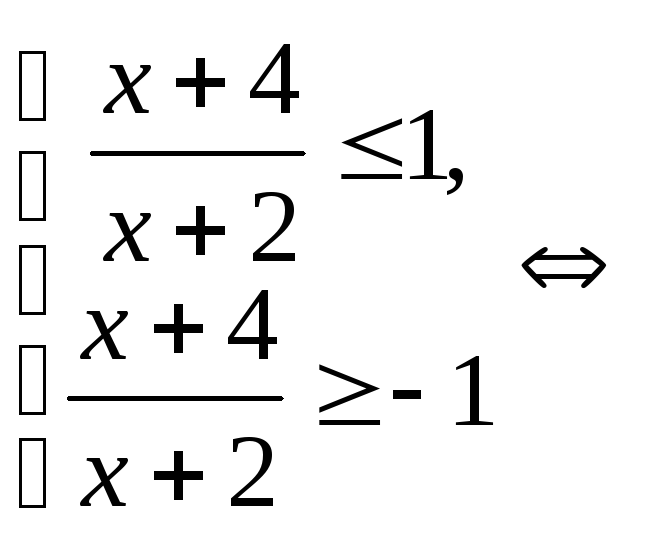
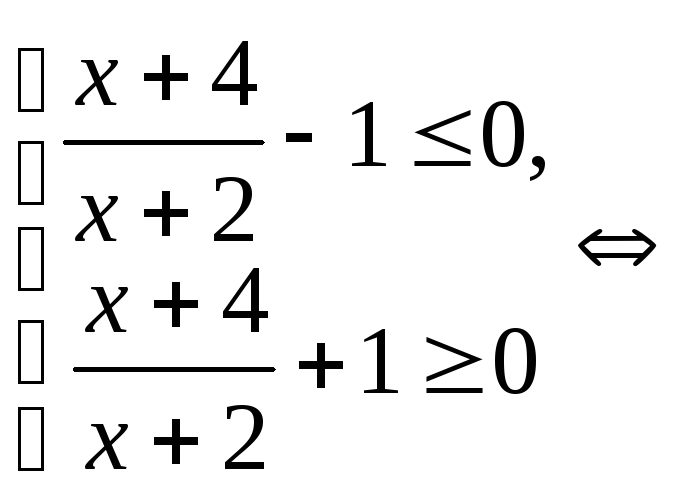
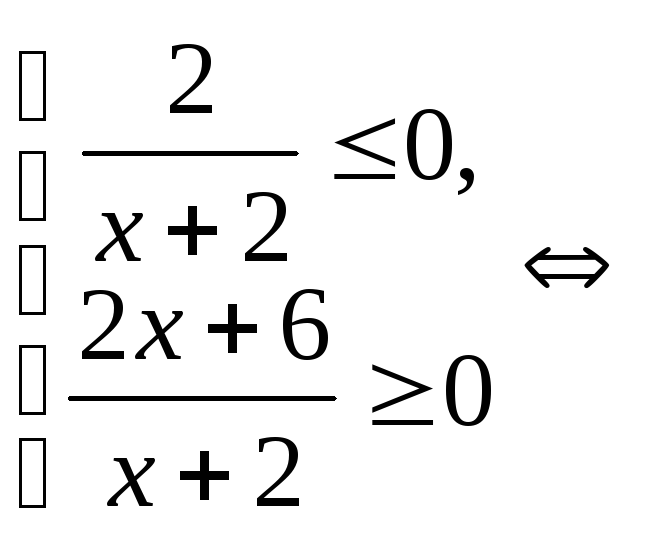
![]()
![]()
Ответ:
![]() .
.
Пример. Решить неравенство
![]() .
.
Решение: Приведем исходное
неравенство к виду
![]() :
:
![]()
Перейдем к равносильной системе:
![]() ,
,
Имеем:

Решение первого неравенства системы
является любое
![]() ,
а решением второго является
,
а решением второго является
![]() или
или
![]()
Ответ:
![]() .
.
