-
Решение простейших уравнений и неравенств: квадратных, рациональных (дробно-рациональных).
Многие уравнения и неравенства часто сводятся к решению линейных и квадратных уравнений и неравенств соответственно. Поэтому кратко повторим основные подходы к их решению.
Корень (решение) уравнения – число, которое при подстановке его в уравнение вместо переменной, превращает данное уравнение в верное равенство.
Решить уравнение, - значит, найти все его корни (решения) или доказать, что корней (решений) нет.
Равносильные уравнения – уравнения, множества корней (решений) которых совпадают, в частности, если оба уравнения не имеют корней, то они равносильны.
Замечание: 1. Если каждый корень
уравнения
является в то же время корнем уравнения
,
полученного после некоторых преобразований
из уравнения
,
то уравнение
называют следствием уравнения
.
2. Если каждое из двух уравнений является следствием другого из них, то такие уравнения являются равносильными.
Линейные
уравнения – уравнения вида
,
где
и
- некоторые числа,
- переменная. Эти уравнения имеют три
различных случая решения (рассмотрим
на примерах):
Пример.
(умножим обе части уравнения на
12).
,
,
,
.
(единственное решение).
Пример.
,
решений нет.
Пример.
;
любое
удовлетворяет последнему уравнению, а значит и исходному. (бесконечно много
решений).
Квадратные
уравнения – уравнения вида
,
где
и
- некоторые числа,
- переменная, при этом
(при
уравнение превращается в линейное.)
Если
или
,
а также в случае одновременного равенства
нулю этих коэффициентов квадратное
уравнение называют неполным и решают
стандартными способами разложения на
множители.
Пример.
или
;
или
.
Пример.
.
Для решения полного квадратного уравнения используют обычную формулу корней квадратного уравнения:
.
Возможны три случая:
1.
;
уравнение имеет два различных
действительных корня
,
;
2.
;
уравнение имеет два одинаковых
действительных корня
;
3.
;
уравнение не имеет действительных
корней.
Замечание. Для решения
приведенного квадратного уравнения,
,
,
часто используют теорему Виета:
,
.
Пример.
.
Рациональные (дробно-рациональные) уравнения.
Определение: Функция вида
,
где
;
- некоторый действительные числа,
называется целой рациональной
функцией.
Целым рациональным уравнением
называется уравнение вида
,
где
- целая рациональная функция.
Теорема 1. Для того чтобы
несократимая дробь
была корнем многочлена
с целыми коэффициентами, необходимо,
чтобы число
было делителем свободного члена
,
а число
- делителем старшего коэффициента
.
Теорема 2. (Теорема Безу) Остаток
от
деления многочлена
на двучлен
равен значению мног4очлена
при
,
то есть
.
При делении многочлена
на двучлен
имеем равенство
.
Оно справедливо, в частности, при
,
то есть
.
Пример. Решить уравнения: 1)
;
2)
;
3)
;
4)
.
Пример. Решить уравнение
.
Решение: Поскольку коэффициенты
уравнения – целые числа, то попробуем
найти хотя бы один целый корень. Делителями
свободного члена являются числа
.
Подстановкой легко убедиться, что
- корень уравнения. Проведем деление
многочленов «уголком»:
|
|
Получили
.
Аналогично, убеждаемся, что
- корень многочлена
,
проведем деление:
Таким образом, исходное уравнение можно записать в виде:
,
Что равносильно совокупности двух уравнений:
Дискриминант второго уравнения
отрицательный, значит, оно не имеет
действительных корней. Итак,
является корнем исходного уравнения.
Для самостоятельного решения:
Решить уравнение:
Ответ: -1, 2.
Дробно-рациональным уравнением
называется уравнение вида
,
где
- многочлены.
Решение дробно-рационального уравнения
сводится к нахождению корней уравнения
и проверке того, что они удовлетворяют
условию
,
то есть рациональное уравнение равносильно
системе:
Пример. Решить уравнения 1)
;
2)
.
Пример. Решить уравнение
.
Решение: Область определения уравнения:
.
Далее будем работать на области
определения уравнения. Умножим обе
части уравнения на
и получим уравнение:
,
.
Пример. Решить уравнение
.
Решение: Область определения уравнения:
.
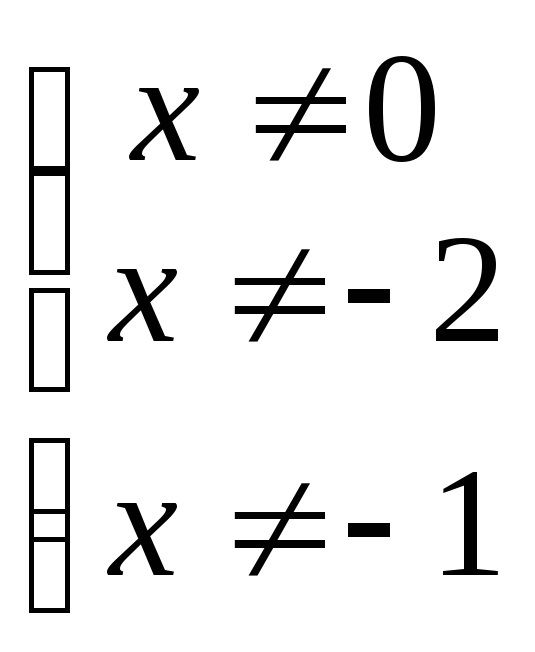Далее будем работать на области
определения уравнения. Заметим, что
;
.
Сделаем замену
.
Тогда исходное уравнение перепишем
следующим образом:
,
,
,
,
Обратная замена:
.
Пример. Решить уравнение
.
Решение: Непосредственно
проверкой устанавливаем, что
не является корнем данного уравнения.
Тогда вынесем
из каждой скобки и перейдем к равносильному
уравнению:
,
.
Сделаем замену:
.
Отсюда:
или
.
,
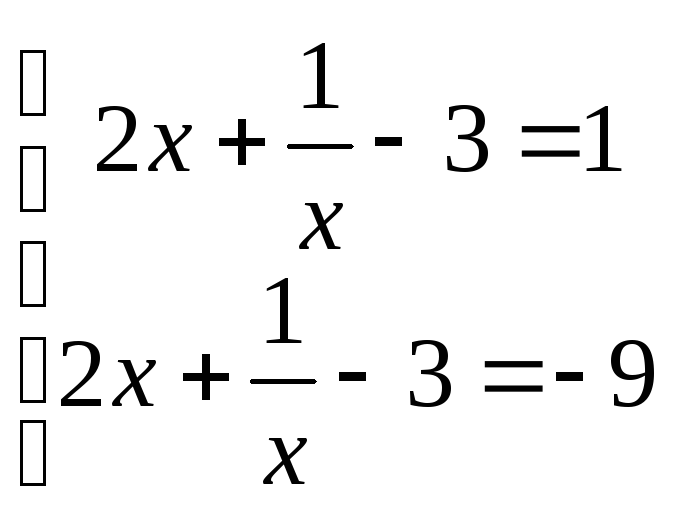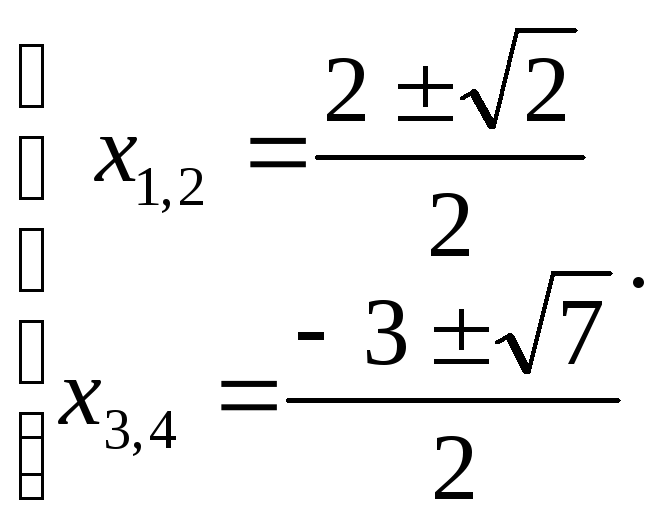
Пример. Решить уравнение
.
Решение: Сгруппируем множители в левой части уравнения так, чтобы при перемножении были равны первый коэффициент и свободный член:
Далее аналогично примеру 10. Так как
не является корнем уравнения, вынесем
его за скобки:
Замена:
,
или
.
.
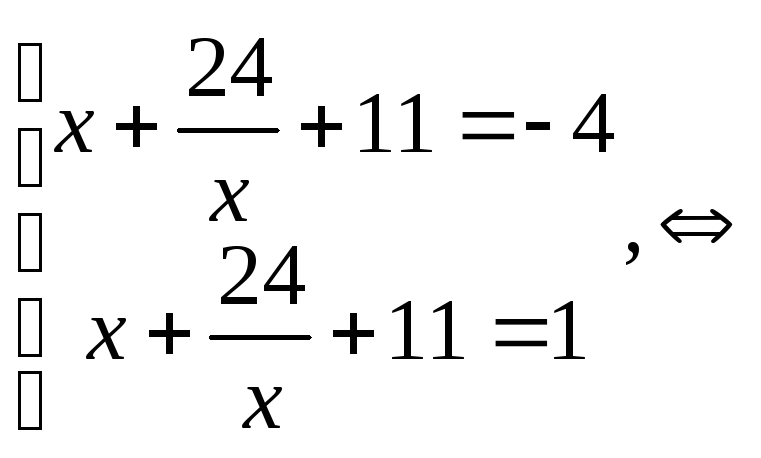
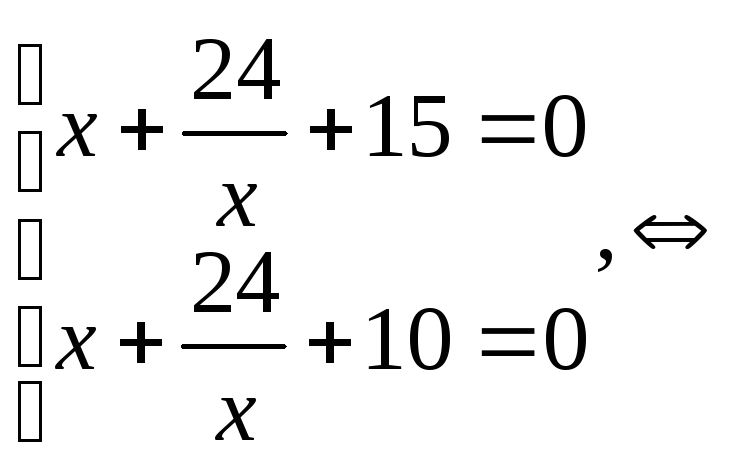
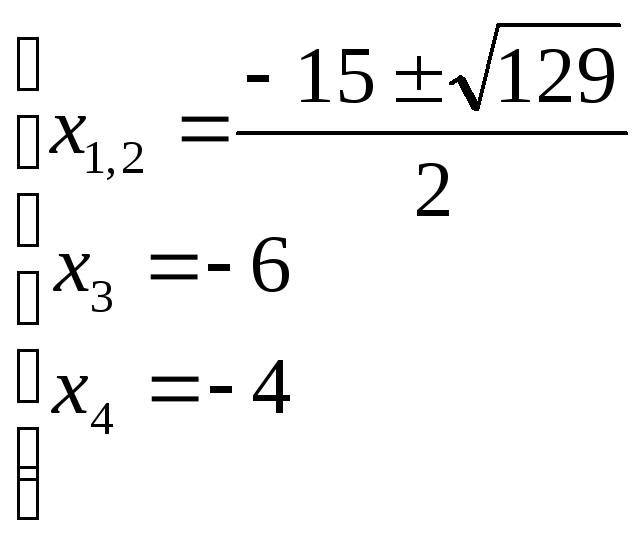Пример. Решить уравнение
.
Решение: Так как
не является корнем уравнения, разделим
обе части уравнения на
,
получим уравнение, равносильное данному:
.
Сгруппируем члены этого уравнения:
.
Введем замену:
,
,
.
или
.
.
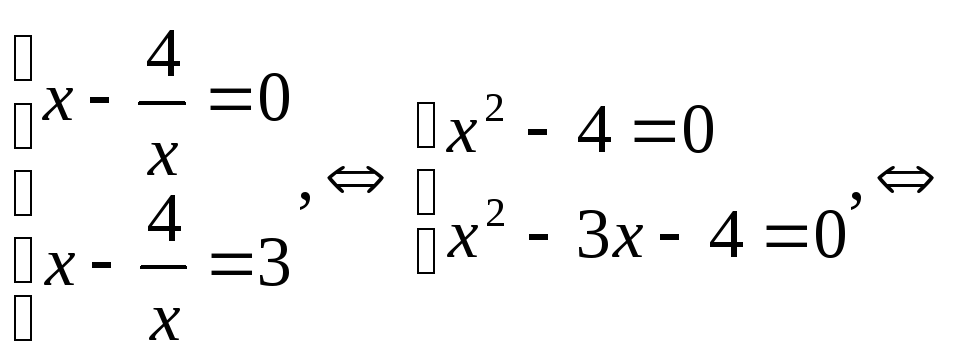
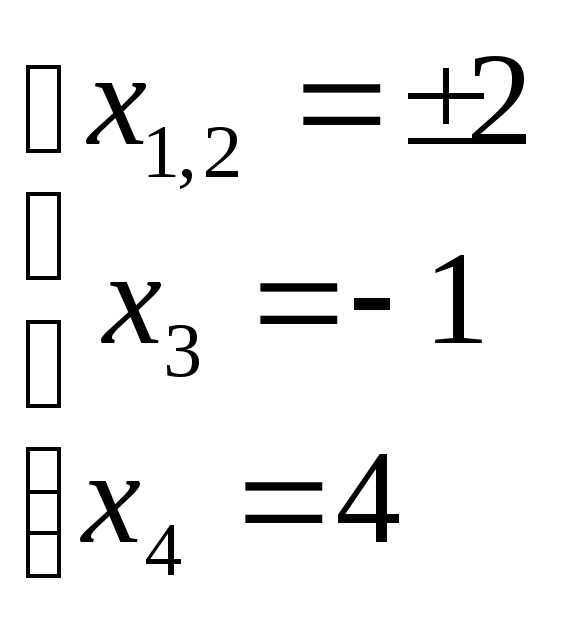Для самостоятельного решения:
1. Решить уравнение:
(Примечание: замена
).
Ответ: -2, 1.
2. Решить уравнение:
.
(Примечание: замена
).
Ответ:
.
Рациональные (дробно-рациональные) неравенства. Метод интервалов для рациональных функций.
Важнейшим методом решения неравенств
является метод интервалов. В 9 классе
изучается метод интервалов, прежде
всего для многочленов. Он основан на
том, что двучлен
положителен при
и отрицателен при
,
то есть меняет знак при переходе через
точку
.
Заметим, что
-
двучлен
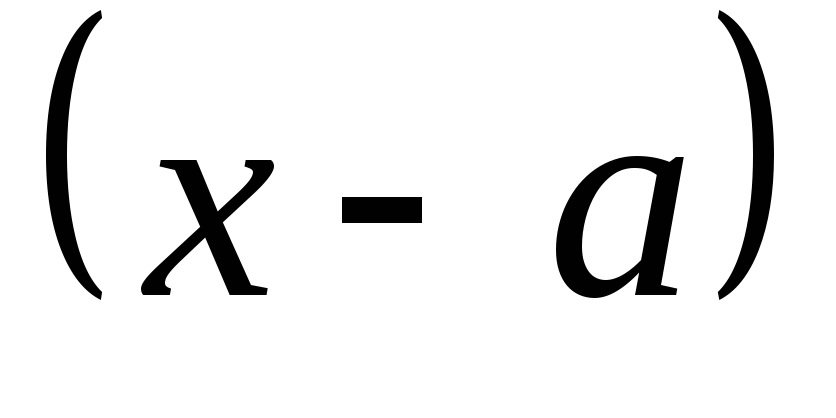в нечетной степени ведет себя так
же, как
, -
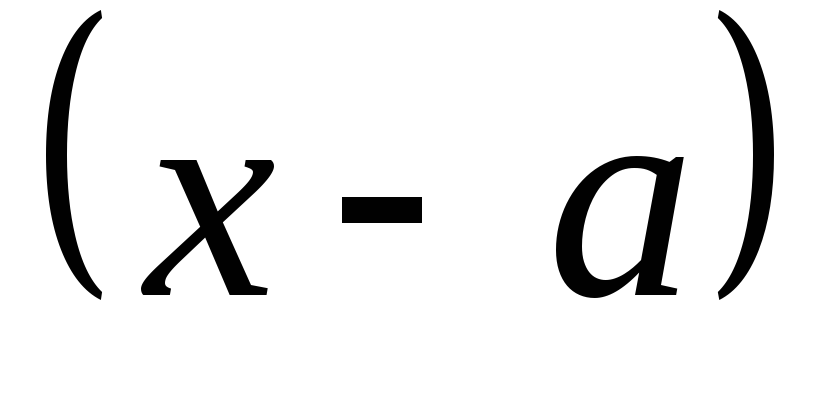двучлен
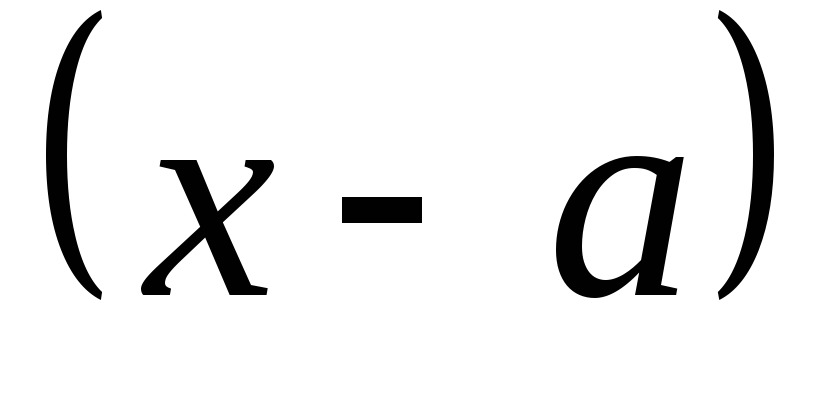в четной степени ведет себя
по-другому: он не меняет знак при
переходе через точку
. -
квадратичный трехчлен, имеющий положительный коэффициент при
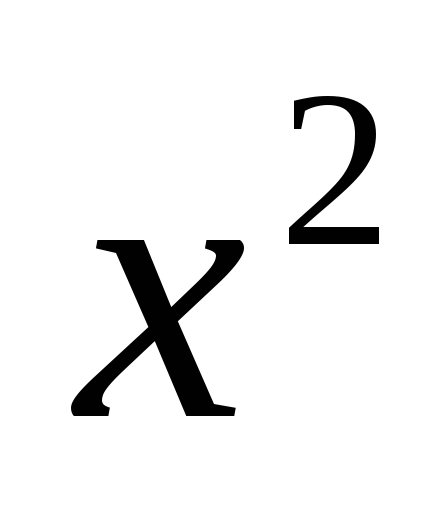и отрицательный дискриминант, всегда
положителен и может быть опущен при
решении любого неравенства. -
при переходе через точку
может изменить знак только один
множитель,
,
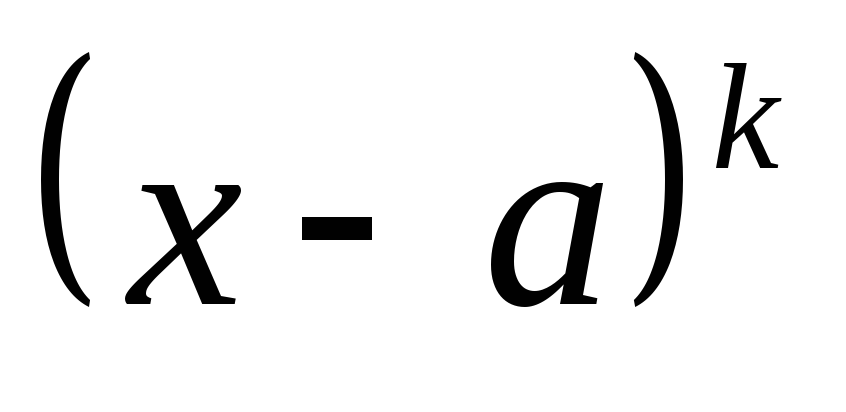выражение
при переходе через точку
знак не меняет.
Пример. а.
Решить неравенство
,
б.
Решение: а. Для решения строгого неравенства наносим на числовую ось нули функции кружочками («дырками»). Далее расставляем знаки, учитывая замечание выше:
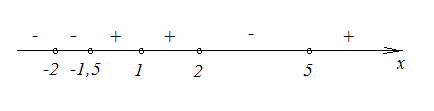
Ответ:
.
б. Вспомним, что по определению,
.
Для решения нестрогих неравенств наносим нули функции на числовую ось точками. Затем расставляем знаки в промежутках.
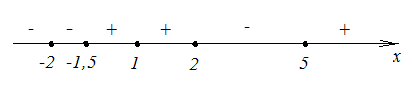
Ответ:
.
Метод интервалов легко распространяется на рациональные функции.
Рациональной называется функция,
которая может быть представлена в виде
частного двух многочленов, то есть в
виде
.
Неравенства называются рациональными, если их правые и левые части являются рациональными функциями.
Заметим, что
,
поэтому метод интервалов применяется
к дроби точно так же, как и к многочленам.
Для нестрого же неравенства имеем:
.
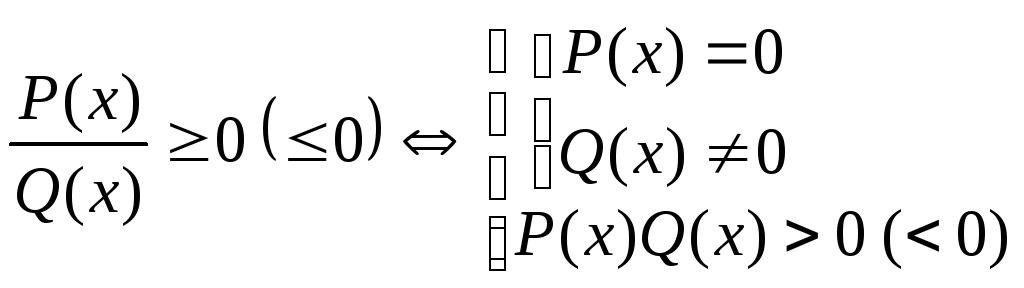При решении нестрогих рациональных неравенств нули числителя наносятся на числовую ось точками, а нули знаменателя - «дырками».
Пример. Решить неравенство
.
Решение: Приведем неравенство к стандартному виду и разложим числитель и знаменатель на множители. Затем решаем методом интервалов:
,
,
,
Ответ:
.
Пример. Найти сумму целых
решений неравенства
.
Решение: Решим неравенство методом интервалов:
.
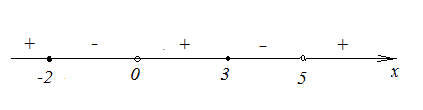
Видно, что целыми решениями являются
числа: -2, -1. 3. 4. Их сумма равна 4.
Ответ: 4.
Для самостоятельного решения:
-
Решить неравенства:
|
|
|
|
|
|
|
|
|
|
|
|
2. Укажите длину промежутка, который является решением неравенства:
Ответ: 9.
3. Найти произведение всех целых решений
неравенства:
.
Ответ:
.