15. N ретті сызықтық теідеулер шешімдері үшін Лиувилль-Остроградский формуласы

Лиувилль формуласы

коэффициен былай анықталады:

(13)

Анықтауыштың туындысын табу ережесін еске алсақ, (13) қатынастың алымы бөлімінің туындысы болып шығады, яғни

Осы қатынасты интегралдасақ,

теңдігін аламыз. Осыдан

немесе

(14)

Осы қатынасты Лиувилль формуласы деп атайды.

Лиувилль формуласын пайдаланып бір шешімі белгілі екінші ретті біртекті сызықты теңдеудің жалпы шешімін құруға болады.

Егер теңдеуініңшешімі белгілі болса, онда Лиувилль формуласы былай жазылады:

немесе

Соңғы теңдікті функциясына көбейтіп интегралдасақ, онда

теңдігінен

теңдігін аламыз. Осыдан

(15)

Мұндағы, функциясы теңдеудің екінші дербес шешімін береді. Оған – теңдеуге қойып көз жеткізуге болады және бұлжәнешешімдер өзара тәуелсіз. Сондықтан, (15) қатынас жалпы шешім болады.

16. Біртекті емес сызықты теңдеулердің жалпы шешімін тұрақты санды вариациялау әдісі (Лагранж әдісі).

Біртексіз теңдеудің жалпы шешімін біртектітеңдеудің жалпы шешімі –түрде іздейміз, бірақ мұндағыС санын х-қа байланысты айнымалы функция деп есептейміз:

(5)

Осы функцияны теңдеуге апарып қоялық:

.

Бұдан

теңдеуін аламыз. Енді осы теңдеуді интегралдасақ, онда

(6)

өрнегін аламыз. Мұнда С₀ – кез келген тұрақты сан. Осы (6) өрнекті (5) қатынасқа апарып қойсақ, онда біртексіз теңдеудің жалпы шешімін аламыз:

(7)

Соңғы шешімді Коши түрінде жазсақ, онда мынандай өрнек аламыз:

(8)

мұнда х₀-тұрақты сан, ал у₀ – кез келген сан деп есептейміз.

18. Біртекті емес сызықты теңдеулердің жалпы шешімінің құрылымы.

берілген біртексіз (1) теңдеуге оралатын болсақ, оның жалпы шешімін табу үшін мынандай әдістерді қолдануға болады.

1⁰. Тұрақты санды вариациялау әдісі (Лагранж әдісі).

Біртексіз (1) теңдеудің жалпы шешімін біртекті (2) теңдеудің жалпы шешімі – (3) түрде іздейміз, бірақ мұндағы С санын х-қа байланысты айнымалы функция деп есептейміз:

(5)

Осы функцияны (1) теңдеуге апарып қоялық:

.

Бұдан

теңдеуін аламыз. Енді осы теңдеуді интегралдасақ, онда

(6)

өрнегін аламыз. Мұнда С₀ – кез келген тұрақты сан. Осы (6) өрнекті (5) қатынасқа апарып қойсақ, онда біртексіз (1) теңдеудің жалпы шешімін аламыз:

(7)

Соңғы шешімді Коши түрінде жазсақ, онда мынандай өрнек аламыз:

(8)

мұнда х₀-тұрақты сан, ал у₀ – кез келген сан деп есептейміз.

19. Біртекті сызықты теңдеулер

Біртекті сызықты теңдеудің шешімдерінің қасиеттерін келтірейік. Коэффициенттері кейбір аралығында үздіксіз болып келетін мына-ретті теңдеуді қарастырайық:

(1)

Ең алдымен ескеретін жәй – біртекті сызықты теңдеудің барлық жағдайда нольдік шешімі бар. Ол шешім

(2)

бастапқы шартты қанағаттандыратын Коши есебінің шешімі: . Бұл шешім жалғыз.

Теорема-1. Егер 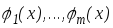функциялары (1) теңдеудіңаралығындағы шешімдері болса, онда олардың сызықты комбинациясы

(3)

сол теңдеудің аралығындағы шешімі болады.

Теорема-2. Егер (1) теңдеудің түріндегі комплекс шешімі бар болса, онда оның нақты және жорамал бөліктері өз алдына сол теңдеудің шешімдерін береді.

Анықтама-1. Егер аралығында анықталған

функциялары үшін бәрі бірдей нөлге тең емес сандары табылып,

(4)

теңдігі орындалса, онда берілген функциялар жиыны аралығында сызықты тәуелді деп аталынады, ал (4) теңдіксандарының тек нөлдік мәндерінде ғана орындалса, онда берілген функциялар жиыныаралығында сызықты тәуелсіз деп аталады.