Лекция №13 _2013г_ Осн-е понятия мат.ст-ки

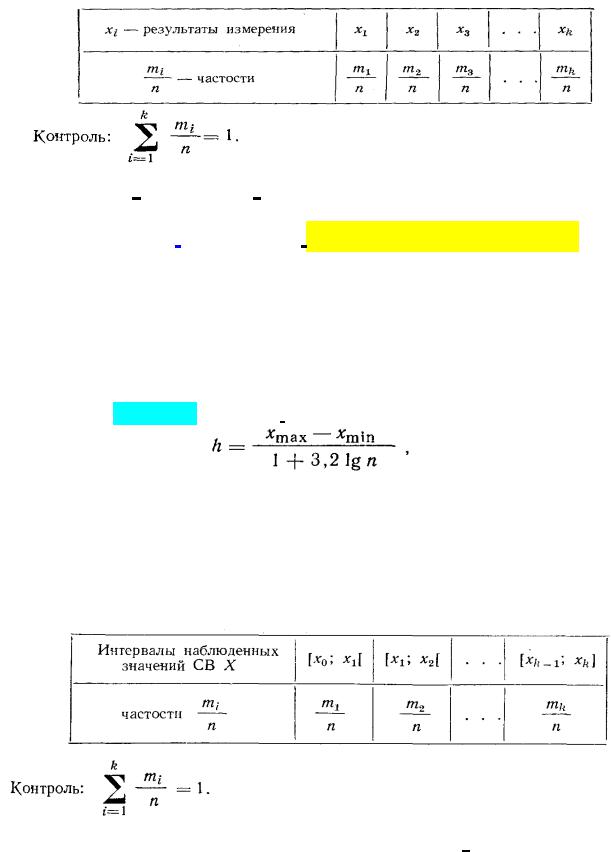
11

Таблица 2.3

Статистический ряд относительных частот (частостей)

Если изучается непрерывная случайная величина, то группировка заключа-

ется в разбиении интервала наблюдённых значений случайной величины на k частичных интервалов равной длины [x0; x1 ], [x1; x2 ], [x2 ; x3 ]..., [xk−1; xk ] и подсчёте

ных значении в частичные интервалы. Количество интервалов выбирается произвольно, обычно не меньше 5 и не больше 15.

Примечание. Для выбора оптимальной длины интервалов, т. е. такой длины

частичных интервалов, при которой статистический ряд не будет очень громоздким и в нем не исчезнут особенности исследуемой случайной величины, можно рекомендовать, например, формулу Стерджеса:

где n — объем выборки; h — длина частичного интервала.

В результате составляется интервальный статистический ряд следующего вида (см. табл.2.4):

Таблица 2.4

Интервальный статистический ряд

Таким образом, можно дать следующее определение статистического закона распределения случайной величины:

12

Перечень вариант (наблюденных значений случайной величины Χ или интервалов наблюденных значений) и соответствующих им частот (частостей) называется статистическим законом распределения случайной величины X.

Заметим, что в теории вероятностей под законом распределения случайной величины понимают соответствие между возможными значениями (или интервалами возможных значений случайной величины) и их вероятностями, а в ма-

тематической статистике статистический закон распределения устанавливает соответствие между наблюденными значениями (или интервалами наблюденных значений) случайной величины и соответствующими им частостями (частотами).

Статистические законы распределения случайных величин и их графическое изображение, которое мы будем рассматривать позже, позволяют визуально про-

извести оценку закона распределения исследуемой случайной величины и вы- двинуть гипотезу о принадлежности его к тому или иному теоретическому закону распределения известному в теории вероятностей.

3. Эмпирическая функция распределения. Графическое представление статистических рядов.

3.1 Эмпирическая функция распределения.

Пусть известно статистическое распределение частот количественного при-

знака X. Введем обозначения: nx - число наблюдений, при которых наблюдалось

значение признака, меньшее x; n – общее число наблюдений (объём выборки).

Очевидно, что относительная частота события X <x равна: w(x) = nx 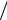n. Из дан-

ного выражения видно, что относительная частота w(x)является функцией за-

данного значения x, так как действительно – если x изменяется, то изменяется и относительная частота (частость). В связи с тем, что относительная частота определяется лишь после проведения испытаний (опыта, эксперимента), то она, как принято говорить, находится эмпирическим (опытным) путём. Поэтому её (функ-

цию w(x)) называют эмпирической. На этом основании в статистике вводят по-

нятие эмпирической функции распределения

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F* (x), определяющую для каждого значения x относительную

частоту события X < x.

Таким образом, в соответствии с данным определением:

где nx - число вариант, меньших x; n – объём выборки.

Следовательно, для того чтобы найти, например, F*(x2 ), надо число вариант,

меньших x2, разделить на объём выборки:

13

(3.2)

В отличие от эмпирической функции распределения выборки F* (x) функ-

цию распределения генеральной совокупности F (x) называют теоретической

функцией распределения. Различие между эмпирической и теоретической

функциями состоит в том, что теоретическая функция F (x) определяет веро-

ятность события X < x, а эмпирическая функция F* (x) определяет относи-

тельную частоту этого же события.

Из теоремы Бернулли следует, что относительная частота события X < x, т.е.

w(x)= F* (x) стремится к вероятности F (x) этого события. Другими словами - при больших объёмах выборки, т.е. числа «n», числа F* (x) и F (x) мало от-

личаются одно от другого, так как lim P[F(x)− F* (x) < ε ]= 1(ε > 0).

n→∞

На основании данного соотношения, следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.

Данный вывод подтверждается тем, что эмпирическая функция распределения F* (x) обладает всеми свойствами теоретической функции распределения F (x). Действительно, из определения эмпирической функции распределения F* (x) вытекают следующие её свойства:

1)значения эмпирической функции принадлежат отрезку [0,1];

2)F* (x) - неубывающая функция;

3) Если x1 – наименьшая варианта, то F*(x)= 0 при x ≤ x1 ; если же xk - наибольшая варианта, то F*(x)=1 при x > xk .

И так, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример. Построить эмпирическую функцию по данному распределению выборки:

14

Решение.

Найдём объём выборки: n = 12+18+30=60.

Из условия примера видно, что наименьшая варианта (наблюдаемое значение x) равна 2. Тогда:

F* (x) = 0 при x ≤ 2.

Значение вариант X < 6 , наблюдалось лишь один раз, а именно значение

Наибольшая варианта (наблюдаемое значение x) равно 10, тогда:

F * (x)= 1 при x > 10.

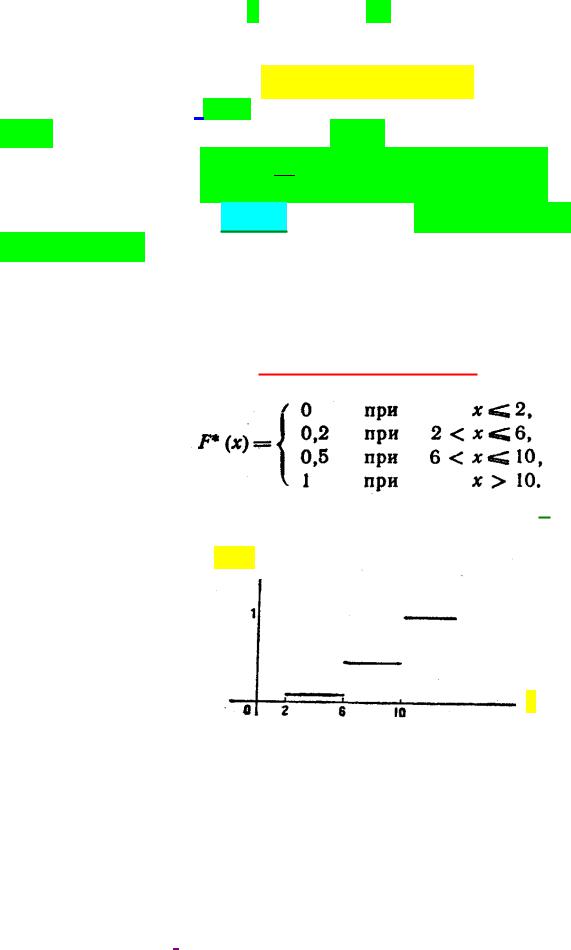
Таким образом, искомая эмпирическая функция, по условию примера, равна:

График искомой эмпирической функции распределения имеет вид, представленный на Рис.3.1.

F*(x)

x

Рис.3.1 График искомой функции распределения примера.

3.2 Графическое представление статистических рядов

Для наглядности, сгруппированные статистические ряды представляют (изо-

бражают) графиками и диаграммами. Наиболее распространёнными графиками являются - полигон и гистограмма, менее распространёнными – кумулята и оги-

ва.

Полигон, кумулята и огива применяются для изображения как дискретных, так и интервальных статистических рядов.

Гистограмма применяется лишь для изображения интервальных статистических рядов.

15

Полигоном частот называют ломаную кривую, отрезки которой

соединяют точки (x1;n1), (x2 ;n2 ), ...., (xk ; nk ). Для построения полигона

частот (относительных частот) на оси абсцисс откладывают варианты xi , а на

оси ординат – соответствующие им частоты ni (относительные частоты (xi ; wi )).

Точки (xi ;ni ) (или (xi ; wi )) соединяют отрезками прямых и получают полигон

частот (или относительных частот).

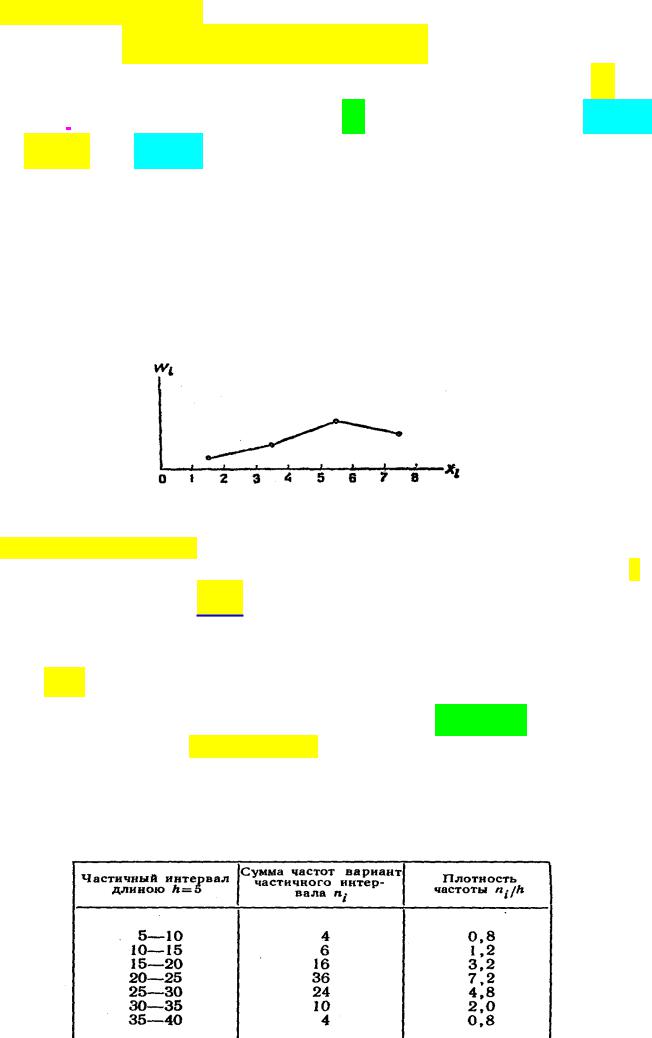
Например, на рисунке 3.2 изображён полигон относительных частот следующего статистического ряда наблюдений (табл.3.1).

Таблица 3.1.

0.4

Рис.3.2 Полигон относительных частот примера табл.3.1.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а

высоты равны отношению ni 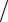h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные

интервалы, а над ними ПРОВОДЯТ ОТРЕЗКИ, ПАРРАЛЕЛЬНЫЕ ОСИ АБСЦИСС НА РАС-

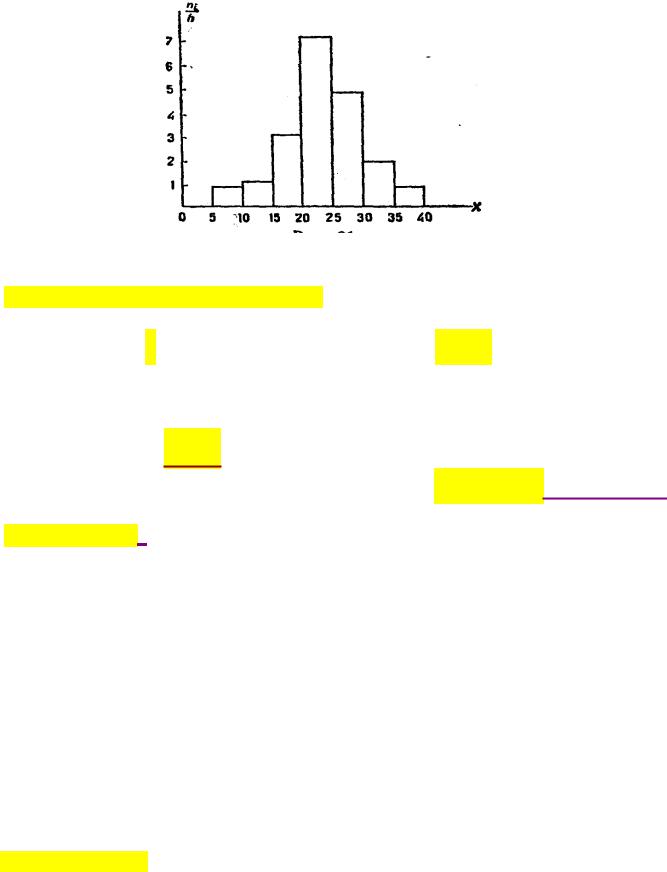
СТОЯНИИ ni 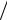h .

Площадь i-го частичного прямоугольника равна hni / h = ni - сумме частот

вариант i-го интервала. Следовательно, площадь гистограммы частот равна

сумме всех частот, т.е. объёму выборки.

На Рис.3.3 изображена гистограмма частот распределения объёма n = 100, приведенного в табл. 3.2.

Таблица 3.2

16

Рис. 3.3. Гистограмма частот примера табл.3.2.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные

интервалы длиною h, а высоты равны отношению wi / h (плотность относи-

тельной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки параллельные оси

абсцисс на расстоянии wi / h .

Площадь i-го частичного прямоугольника равна hwi / h = wi - относитель-

ной частоте вариант, попавших в i - й интервал.

Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Для построения кумуляты на оси абсцисс откладывают наблюденные значения случайной величины X, на оси ординат — накопленные частости. Накопленной частостью в точке х называется суммарная частость членов статистического ряда, значения которых меньше х, т. е. значения накопленных частостей являются значениями эмпирической функции распределения F*(x). В теории вероятностей кумуляте соответствует график функции распределения F(х) =Р(Х<х).

Если при построении кумуляты оси координат поменять местами, т. е.

на горизонтальной оси откладывать значения эмпирической функции распределения F*(x), а на вертикальной — наблюденные значения случайной величины X, то полученная ломаная линия называется огивой.

На рис. 3.3 и 3.4 изображены графики кумуляты и огивы интервального ряда, представленного в таблице 3.3.

17

Таблица 3.3

Результаты исследования стоимости акций

При построении использованы значения эмпирической функции распределения F*(x):

18

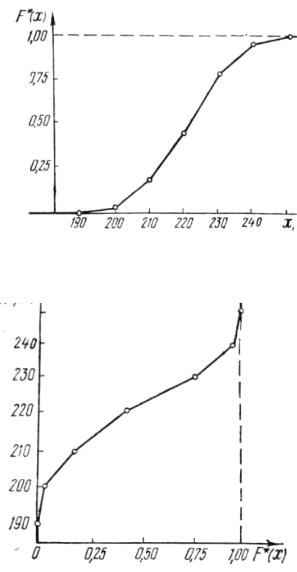
Рис.3.3 График кумуляты для примера таблицы 3.3

Рис.3.4 График огивы для примера таблицы 3.3

Автор: к.т.н., доцент В.Е.Куприянов

30.08.2013г.

19