1. Распределение Эрланга

Р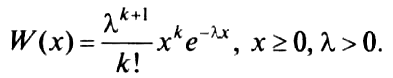аспределение Эрланга являетсядвухпараметрическим законом распределения, используемым для вероятностного задания положи­тельных непрерывных случайных величин, что свойственно значительному большинству вероятностных задач. Плотность вероятности случайной величины, имеющей распределение Эрланга, определяется формулой

(2.1)

Как следует из формулы (2.1), плотность вероятности зависит от значения двух параметров k и λ. Параметр k называют порядком распределения Эрланга, и он может иметь целочисленные значения k = 0, 1,2,...

Математическое ожидание и дисперсия случайной величины, име­ющей распределение Эрланга, определяется формулами:

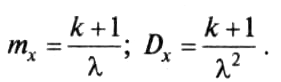
(2.2)

Получим функцию распределения F(x) для случайной величины, имеющей распределение Эрланга первого порядка k = 1. Подставляя формулу (2.1) в формулу взаимосвязи функции и плотности распределения, для F(x) получим:

(2.3)

Используем метод интегрирования по частям. Для этого введем обозначения:

Отсюда

В соответствии с принятыми обозначениями получим:

(2.4)

Формула (2.4) позволяет легко определить вероятность попадания в заданный интервал непрерывной случайной величины, имеющей распределение Эрланга первого порядка.

Графики плотности вероятности распределения Эрланга нулевого k = 0, первого k = 1 и второго порядка k = 2 при λ = 2 приведены на Рис.2.1 а), а графики функции распределения на Рис.2.2 b).

f(x)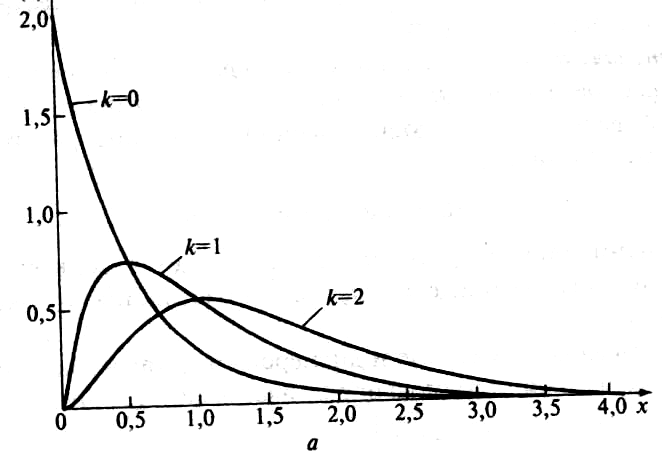

Рис.2.1а) Графики плотности вероятности распределения Эрланга

Рис.2.1b) Графики функции распределения Эрланга

При более высоком порядке распределения Эрланга формула для функции распределения получается более сложной и в лекции не рассматривается.

3. Показательный (экспоненциальный) закон распределения.

Показательное распределениеявляется частным случаем распределения Эрланга приk= 0.

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной вели­чины X. которое описывается плотностью

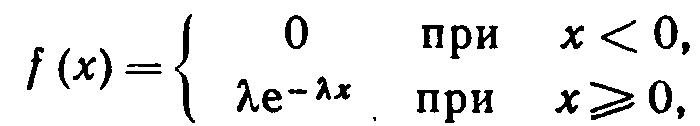
(3.1)

где λ – постоянная положительная величина.

Из выражения (3.1), следует, что показательное распределение определяется одним параметром λ.

Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от боль­шего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значе­ния) разумеется, проще оценить один параметр, чем два или три и т. д. Примером непрерывной случайной вели­чины, распределенной по показательному закону, может служить время между появлениями двух последователь­ных событий простейшего потока.

Найдем функцию распределения показательного закона.

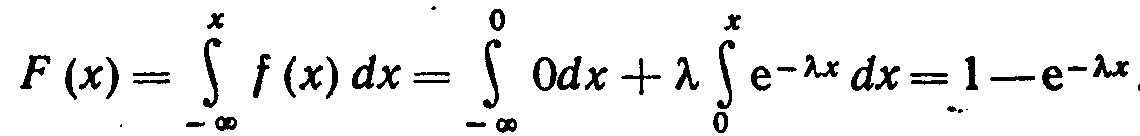
И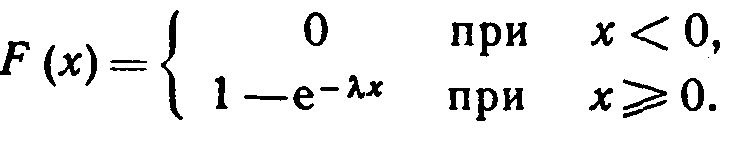так

(3.2)

Графики плотности и функции распределения показа­тельного закона изображены на рис. 3.1.

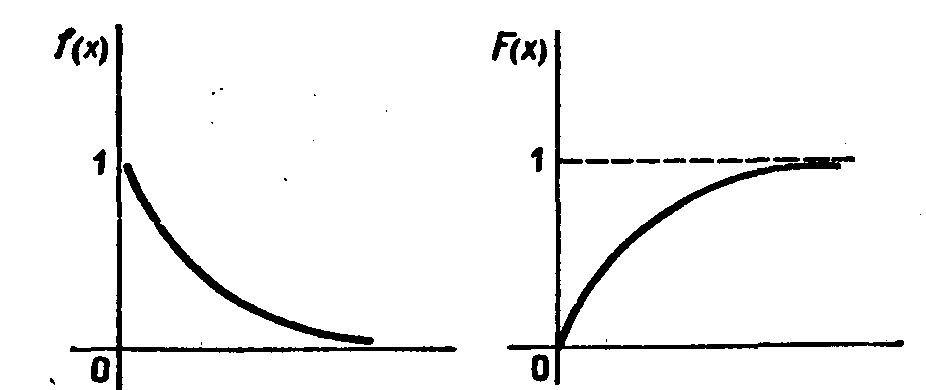
Рис.3.1.Графики плотности и функции распределения показательного закона

Найдем вероятность попадания в интервал (а, b) непрерывной случайной величины X, которая распреде­лена по показательному закону, заданному функцией распределения

Используем известную формулу вычисления вероятности попадания случайной величины в заданный интервал, а именно:

Учитывая, что получим:

(3.3)

Значения функции можно находить по таблице.