4

«Утверждаю»

Заведующий кафедрой

«Управление качеством и

техническое регулирование» ВлГУ ________Ю.А. Орлов

«__»_______2013 г.

Л Е К Ц И Я

по дисциплине «Теория вероятностей, математическая статистика» для бакалавров направления 221400.62 «Управление качеством»

Тема № 2 Случайные величины и их законы распределения

Занятие № 2.10Основные законы распределения вероятностей непрерывных случайных величин

Вид занятия:лекция (12)

Литература: 1). Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб.пособие для вузов.-8-е изд.,стер.-М.:Высш.шк.,2002-479 с. (122-123,149-151,146). 2.) Вентцель Е.С. Теория вероятностей . Учебник М.: Гос.издат.физ.мат.лит-ры., 1958-464с.(99-101,309-310).

Владимир 2013 план

проведения занятия

№ п/п	Учебные вопросы занятия	Время, мин.
I. II	Вводная часть: Объявление темы, темы занятия. Постановка учебных целей занятия. Основная часть.	2-3 75
	Закон равномерного распределения вероятностей. Показательный закон распределения. Распределение хи –квадрат и Стьюдента. Распределение Релея
111	Заключительная часть	2-3
	Подведение итогов занятия. Выдача задания на самостоятельную работу.

Материал основной части лекции

1. Закон равномерного распределения вероятностей.

При решении задач, которые выдвигает практи­ка, приходится сталкиваться с различными распределе­ниями непрерывных случайных величин. Плотности рас­пределений непрерывных случайных величин называют также законами распределений. Часто встречаются, на­пример, законы равномерного, нормального, показатель­ного и других распределений.

Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Найдем плотность равномерного распределения f(x), считая, что все возможные значения случайной величины заключены в интерва­ле (а, b), на котором функция f(x) сохраняет постоянные значения:

По условию, Χ не принимает значений вне интервала (а, b), поэтому f(x)=0 при x < α и x > b.

Найдем постоянную С. Так как все возможные значения слу­чайной величины принадлежат интервалу (а, b), то должно выпол­няться соотношение

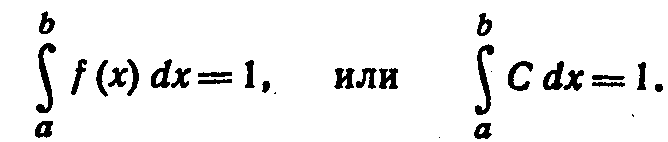
Отсюда

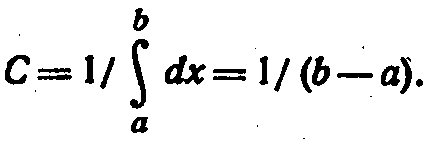
Итак, искомая плотность вероятности равномерного распределе­ния

(1.1)

График плотности равномер­ного распределения изображен на рис. 1.1.

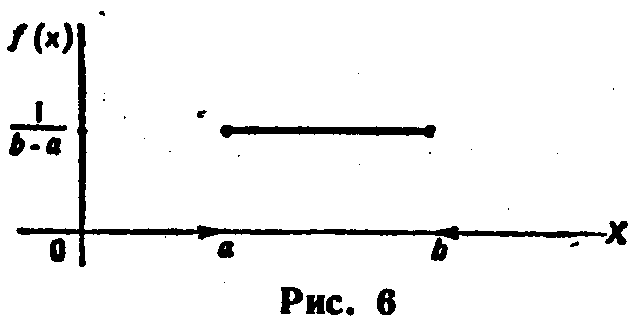
Рис.1.1. График плотности распределения равномерного закона

Для интегральной функции распределения в соответствии с формулой взаимосвязи функции и плотности распределения, можно записать:

О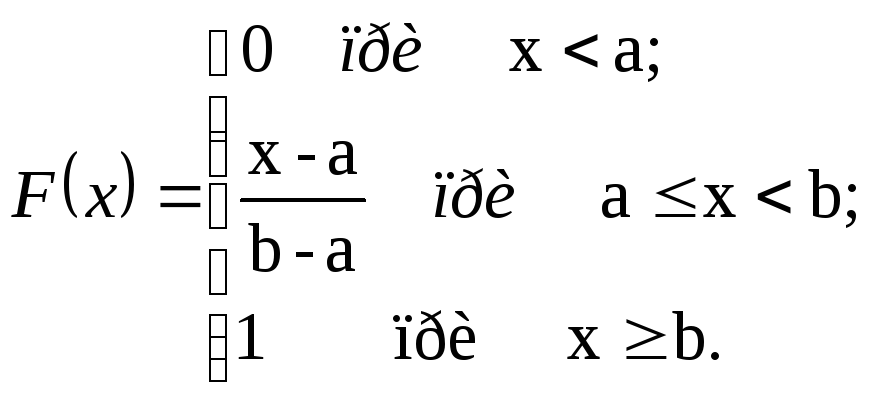кончательно с учётом свойств интегральной функции распределения для получим формулу

(1.2)

График функции распре­деления представлен на рис. 2.

Из формул (1) и (2) следует, что равномерное распределение является двухпараметрическим законом распределения, так как плотность и функция распределения определяются двумя параметрами «a» и «b», ограничивающими нижюю и верхнюю границу области возможных значений случайной величины.

Определим математическое ожидание и дисперсию случайной величины, имеющей равномерное распределение:

(1.3)

Из формулы (3) следует, что при равномерном распределении математическое ожидание случайной величины равно середине интервала, определяющего область её возможных значений.

Найдём дисперсию по формуле:

После разложения разности кубов на сомножители и вычитания дробей для дисперсии получим:

(1.4)

Среднеквадратичное отклонениеравномерно распределённой случайной величины будет равно:

(1.5)

Замечание. Обозначим че­рез R непрерывную случайную ве­личину, распределенную равномер­но в интервале (0, 1), а через r — ее возможные значения. Ве­роятность попадания величины R (в результате испытания) в интервал (с, d), принадлежащий интер­валу (0, 1), равна его длине:

Действительно, плотность рассматриваемого равномерного рас­пределения

Следовательно, вероятность попадания случайной величины R в ин­тервал (с, d) (см. Лекцию 2.8)