
- •Оглавление
- •Введение
- •Задания на контрольную работу по теме «Интегральное исчисление функции нескольких переменных. Векторный анализ. Элементы теории векторного поля»
- •Содержание теоретического материала и ссылки на литературу
- •Справочный материал к выполнению контрольной работы
- •1. Двойной интеграл
- •1.1. Вычисление двойного интеграла в декартовых координатах
- •1.2. Вычисление двойного интеграла в полярных координатах
- •1.3. Некоторые приложения двойных интегралов
- •2. Тройной интеграл
- •2.1. Вычисление тройного интеграла в декартовых координатах
- •2.2. Вычисление тройного интеграла в цилиндрических координатах
- •2.3. Некоторые приложения тройных интегралов
- •3. Криволинейный интеграл II рода (по координатам)
- •4. Векторная функция скалярного аргумента
- •5. Векторное поле
- •5.1. Поток векторного поля через поверхность
- •5.2. Формула Остроградского-Гаусса. Дивергенция
- •6. Потенциальные и соленоидальные векторные поля
- •6.1. Ротор векторного поля
- •6.2. Потенциальное векторное поле и его потенциал
- •6.3. Соленоидальное векторное поле
- •Решение примерного варианта контрольной работы
- •Рекомендуемая литература
1.2. Вычисление двойного интеграла в полярных координатах
Пусть область Dзадается
в полярных координатах системой
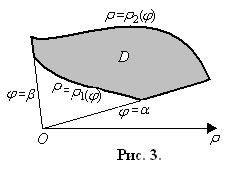
неравенств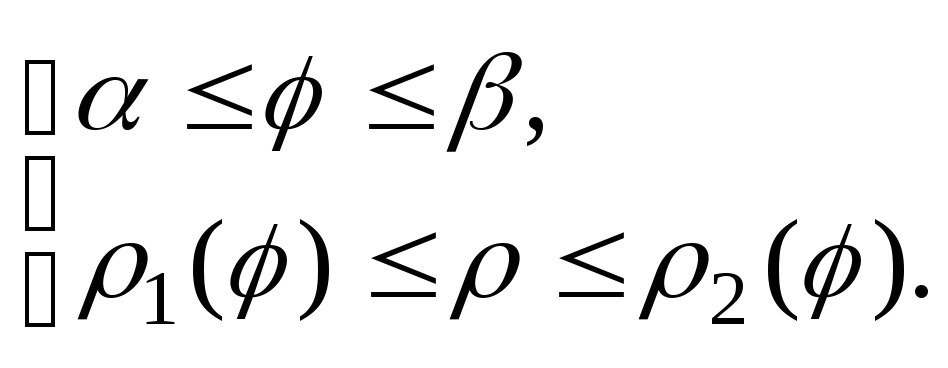 Такая область (рис. 3) являетсяправильной
в полярной системе координат(каждый
луч, выходящий из полюса, пересекает
границу области не более, чем в 2-xточках, за исключением участков границы,
совпадающих с некоторым полярным лучом).
Такая область (рис. 3) являетсяправильной
в полярной системе координат(каждый
луч, выходящий из полюса, пересекает
границу области не более, чем в 2-xточках, за исключением участков границы,
совпадающих с некоторым полярным лучом).
 Преобразование
двойного интеграла по областиDк полярным координатам осуществляется
при помощи формул
Преобразование
двойного интеграла по областиDк полярным координатам осуществляется
при помощи формул
![]() :
:
![]() .
.
Полученный двойной интеграл в полярных координатах может быть сведен к повторному интегралу при помощи неравенств, задающих область D. В результате получаем формулу перехода от двойного интеграла к повторному интегралу в полярных координатах:
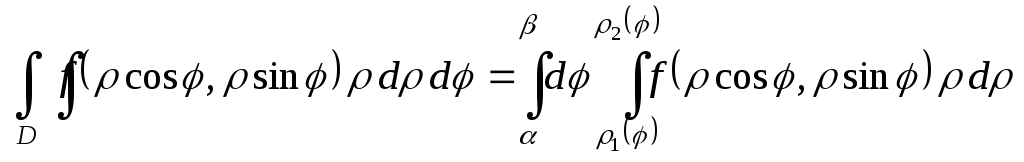 .
.
1.3. Некоторые приложения двойных интегралов
Если подынтегральная функция f (x, y) 1, то двойной интеграл от функции f (x, y) по области D равен площади области интегрирования:
![]() .
.
Если
область D
занята тонкой пластинкой и
![]() – поверхностная плотность распределения
неоднородного материала (т.е. масса
единицы площади), то при помощи двойного
интеграла можно вычислитьмассу
пластинки,
ее статические
моменты относительно осей координат
и другие величины.
– поверхностная плотность распределения
неоднородного материала (т.е. масса
единицы площади), то при помощи двойного
интеграла можно вычислитьмассу
пластинки,
ее статические
моменты относительно осей координат
и другие величины.
Масса
пластинки:
m
=
![]() .
.
Статический момент относительно оси Ox:
![]() . (1)
. (1)
Статический
момент относительно оси Oy:
My
=
![]() .
.
Все перечисленные интегралы можно вычислить в декартовых либо в полярных координатах, переходя к соответствующему повторному интегралу.
2. Тройной интеграл
2.1. Вычисление тройного интеграла в декартовых координатах
Пусть функция 3-х переменных u = f (x, y, z)
задана и непрерывна в замкнутой областиV![]() xOyz.
Тройной интеграл от этой функции по
областиV имеет
вид:
xOyz.
Тройной интеграл от этой функции по
областиV имеет
вид:![]() ,
где
,
где
![]() .
.
Е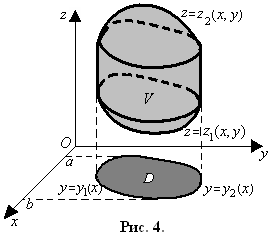 сли
областьV– правильная
в направлении осиOz,
то ее можно задать системой неравенств:
сли
областьV– правильная
в направлении осиOz,
то ее можно задать системой неравенств:
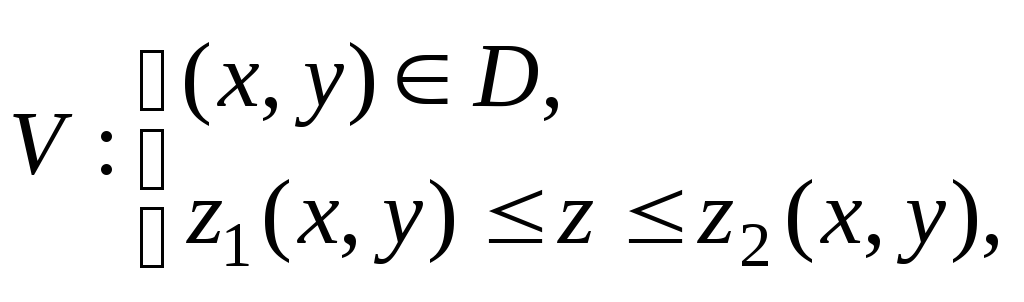
где z = z1 (x, y) иz = z2 (x, y) – это уравнения поверхностей, ограничивающих область (тело)V соответственно снизу и сверху (рис. 4).
Если область Dможно
задать системой неравенств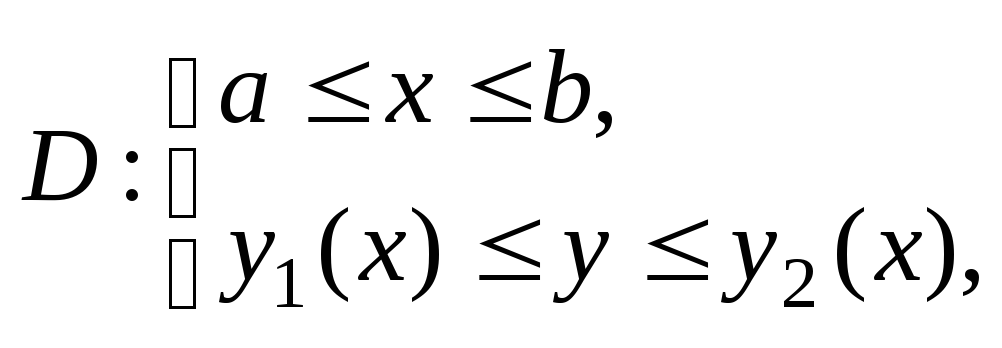 то
то

В этом случае тройной интеграл от функции u = f (x, y, z) по области V можно вычислить при помощи трехкратного повторного интеграла:
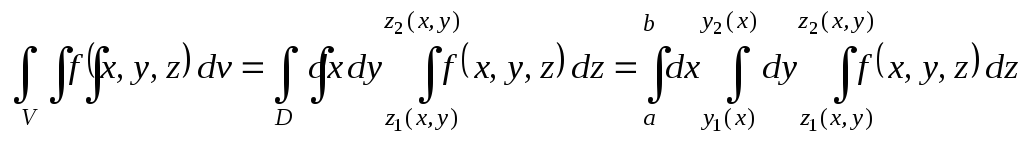 .
.
Здесь каждый внутренний интеграл вычисляется по «своей» переменной интегрирования в предположении, что переменные интегрирования внешних интегралов остаются постоянными.
Существует всего 6 вариантов сведения тройного интеграла к трехкратному в декартовых координатах (в зависимости от выбранного порядка интегрирования).
2.2. Вычисление тройного интеграла в цилиндрических координатах
Цилиндрические координаты точки М в
пространстве– это ее полярные
координаты на плоскостиxOyи координатаz, т.е.![]() .
.
Преобразование тройного интеграла по
области V к
цилиндрическим координатам осуществляется
при помощи формул![]() ,
,![]() ,
,![]() :
:![]()
Если область Vзадана
системой неравенств: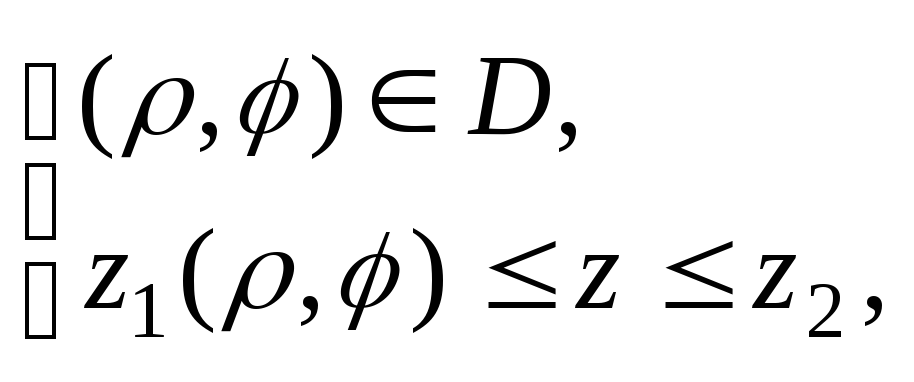 причем
причем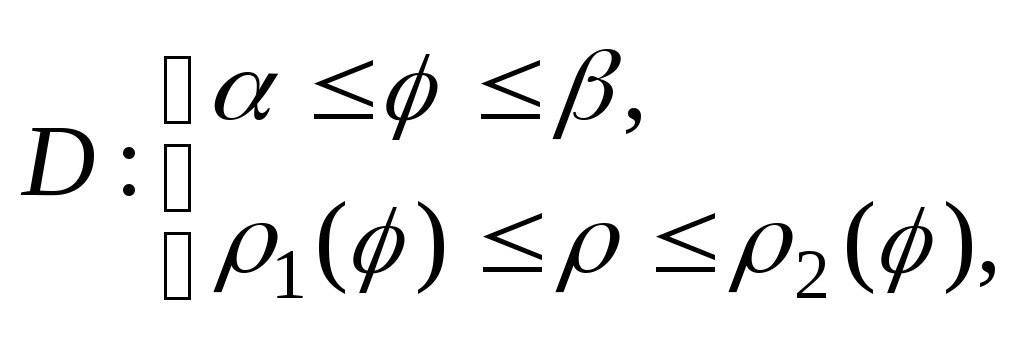 тоV:
тоV:
Вычисление тройного интеграла по области V в цилиндрических координатах сводится к вычислению трехкратного интеграла в соответствии с записанной системой неравенств для областиV:
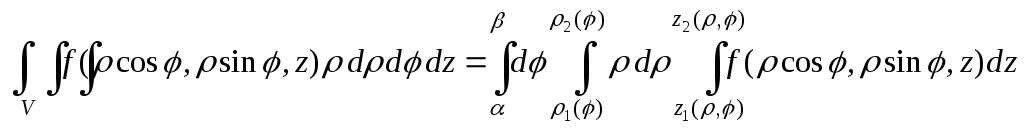 .
.
2.3. Некоторые приложения тройных интегралов
Если
подынтегральная функция f (x, y, z)
1, то тройной интеграл от нее по области
V
равен мере
области интегрирования – объему
пространственного тела,
занимающего область V:
![]() .
.
Если
![]() – это плотность неоднородного материала
(т.е. масса единицы объема), из которого
изготовлено тело, то при помощи тройного
интеграла можно вычислитьмассу
тела, его
статические
моменты относительно координатных
плоскостей
и другие величины. Например, формула
для вычисления массы тела имеет вид:
– это плотность неоднородного материала
(т.е. масса единицы объема), из которого
изготовлено тело, то при помощи тройного
интеграла можно вычислитьмассу
тела, его
статические
моменты относительно координатных
плоскостей
и другие величины. Например, формула
для вычисления массы тела имеет вид:
![]() . (2)
. (2)
