
черняк
.pdf
1956/Q |
2,90 |
4,13 |
2,927 |
1981/Q |
11,3 |
7,40 |
17,577 |
1957/Q |
4,32 |
3,93 |
2,933 |
1981/Q |
4,2 |
8,23 |
13,587 |
1957/Q |
2,85 |
4,10 |
3,000 |
1982/Q |
2,5 |
8,83 |
14,227 |
1957/Q |
2,83 |
4,23 |
3,233 |
1982/Q |
9,5 |
9,43 |
14,513 |
1957/Q |
2,81 |
4,93 |
3,253 |
1982/Q |
2,8 |
9,90 |
11,007 |
1958/Q |
5,57 |
6,30 |
1,863 |
1982/Q |
0,0 |
10,6 |
9,287 |
1958/Q |
0,00 |
7,36 |
0,940 |
1983/Q |
1,63 |
10,3 |
8,653 |
1958/Q |
0,00 |
7,33 |
1,323 |
1983/Q |
5,2 |
10,1 |
8,803 |
1958/Q |
1,38 |
6,36 |
2,163 |
1983/Q |
4,0 |
9,36 |
9,460 |
1959/Q |
0,00 |
5,83 |
2,570 |
1983/Q |
3,9 |
8,53 |
9,430 |
1959/Q |
1,37 |
5,10 |
3,083 |
1984/Q |
5,8 |
7,86 |
9,687 |
1959/Q |
2,74 |
5,26 |
3,577 |
1984/Q |
3,0 |
7,43 |
10,557 |
1959/Q |
1,36 |
5,60 |
3,990 |
1984/Q |
3,8 |
7,43 |
11,390 |
1960/Q |
0,00 |
5,13 |
3,933 |
1984/Q |
3,0 |
7,30 |
9,267 |
1960/Q |
2,71 |
5,23 |
3,697 |
1985/Q |
4,8 |
7,23 |
8,477 |
1960/Q |
0,00 |
5,53 |
2,937 |
1985/Q |
2,6 |
7,30 |
7,923 |
1960/Q |
2,69 |
6,26 |
2,297 |
1985/Q |
2,2 |
7,20 |
7,900 |
1961/Q |
0,00 |
6,80 |
2,003 |
1985/Q |
5,1 |
7,03 |
8,103 |
1961/Q |
0,00 |
7,00 |
1,733 |
1986/Q |
- |
7,03 |
7,827 |
1961/Q |
2,67 |
6,76 |
1,683 |
1986/Q |
1,09 |
7,16 |
6,920 |
1961/Q |
0,00 |
6,20 |
2,400 |
1986/Q |
2,1 |
6,96 |
6,207 |
1962/Q |
2,65 |
5,63 |
2,457 |
1986/Q |
2,8 |
6,83 |
6,267 |
1962/Q |
0,00 |
5,53 |
2,607 |
1987/Q |
5,0 |
6,60 |
6,220 |
1962/Q |
2,64 |
5,56 |
2,847 |
1987/Q |
4,6 |
6,26 |
6,650 |
1962/Q |
0,00 |
5,53 |
2,923 |
1987/ |
4,2 |
6,00 |
6,843 |
1963/Q |
1,31 |
5,76 |
2,967 |
1987/ |
3,1 |
5,83 |
6,917 |
1963/Q |
1,30 |
5,73 |
2,963 |
1988/Q |
3,1 |
5,70 |
6,663 |
1963/Q |
1,30 |
5,50 |
3,330 |
1988/ |
5,1 |
5,46 |
7,157 |
1963/Q |
2,59 |
5,56 |
3,453 |
1988/ |
5,0 |
5,46 |
7,983 |
1964/Q |
0,00 |
5,46 |
3,463 |
1988/ |
3,9 |
5,33 |
8,470 |
1964/Q |
1,29 |
5,20 |
3,490 |
1989/Q |
4,9 |
5,20 |
9,443 |
1964/Q |
1,28 |
5,00 |
3,457 |
1989/ |
6,1 |
5,23 |
9,727 |
1964/Q |
2,56 |
4,96 |
3,577 |
1989/ |
2,2 |
5,23 |
9,083 |
1965/Q |
0,00 |
4,90 |
3,973 |
1989/ |
4,7 |
5,36 |
8,613 |
1965/Q |
3,81 |
4,66 |
4,077 |
1990/Q |
7,2 |
5,30 |
8,250 |
1965/Q |
0,00 |
4,36 |
4,073 |
1990/ |
4,0 |
5,33 |
8,243 |
1965/Q |
3,78 |
4,10 |
4,167 |
1990/ |
7,9 |
5,70 |
8,160 |
1966/Q |
3,74 |
3,86 |
4,557 |
1990/ |
5,0 |
6,13 |
7,743 |
1966/Q |
2,47 |
3,83 |
4,913 |
1991/Q |
1,7 |
6,60 |
6,427 |
1966/Q |
4,90 |
3,76 |
5,410 |
1991/ |
3,5 |
6,83 |
5,863 |
1966/Q |
1,21 |
3,70 |
5,563 |
1991/ |
2,9 |
6,86 |
5,643 |
1967/Q |
1,21 |
3,83 |
4,823 |
1991/ |
3,4 |
7,10 |
4,817 |
1967/Q |
3,62 |
3,83 |
3,990 |
1992/Q |
2,5 |
7,36 |
4,023 |
1967/Q |
3,58 |
3,80 |
3,893 |
1992/ |
2,8 |
7,60 |
3,770 |
1967/Q |
4,73 |
3,90 |
4,173 |
1992/ |
2,8 |
7,63 |
3,257 |
1968/Q |
3,51 |
3,73 |
4,787 |
1992/ |
3,3 |
7,36 |
3,037 |
1968/Q |
4,63 |
3,56 |
5,980 |
1993/Q |
2,8 |
7,13 |
3,040 |
1968/Q |
4,58 |
3,53 |
5,943 |
1993/ |
2,7 |
7,06 |
3,000 |
1968/Q |
5,65 |
3,40 |
5,917 |
1993/ |
1,9 |
6,80 |
3,060 |
1969/Q |
5,57 |
3,40 |
6,567 |
1993/ |
3,5 |
6,63 |
2,990 |
237
1969/Q |
5,50 |
3,43 |
8,327 |
1994/Q |
2,1 |
6,56 |
3,213 |
1969/Q |
5,42 |
3,56 |
8,983 |
1994/ |
2,1 |
6,20 |
3,940 |
1969/Q |
6,41 |
3,56 |
8,940 |
1994/ |
3,7 |
6,00 |
4,487 |
1970/Q |
6,31 |
4,16 |
8,573 |
1994/ |
2,1 |
5,63 |
5,167 |
1970/Q |
5,18 |
4,76 |
7,880 |
1995/Q |
2,9 |
5,46 |
5,810 |
1970/Q |
4,10 |
5,16 |
6,703 |
1995/ |
3,1 |
5,66 |
6,020 |
1970/Q |
6,07 |
5,83 |
5,567 |
1995/ |
1,8 |
5,66 |
5,797 |
1971/Q |
2,00 |
5,93 |
3,857 |
1995/ |
2,0 |
5,56 |
5,720 |
1971/Q |
4,96 |
5,90 |
4,563 |
1996/Q |
4,1 |
5,53 |
5,363 |
1971/Q |
2,95 |
6,03 |
5,473 |
1996/ |
3,0 |
5,50 |
5,243 |
1971/Q |
2,93 |
5,93 |
4,750 |
1996/ |
2,5 |
5,26 |
5,307 |
1972/Q |
2,90 |
5,76 |
3,540 |
1996/ |
3,5 |
5,33 |
5,280 |
1972/Q |
2,88 |
5,70 |
4,300 |
1997/Q |
1,7 |
5,23 |
5,277 |
1972/Q |
3,81 |
5,56 |
4,740 |
1997/ |
1,0 |
5,00 |
5,523 |
1972/Q |
3,78 |
5,36 |
5,143 |
1997/ |
2,4 |
4,86 |
5,533 |
1973/Q |
8,38 |
4,93 |
6,537 |
1997/ |
1,4 |
4,66 |
5,507 |
1973/Q |
7,30 |
4,93 |
7,817 |
1998/Q |
0,4 |
4,63 |
5,520 |
1973/Q |
8,94 |
4,80 |
10,560 |
1998/ |
1,9 |
4,40 |
5,500 |
1973/Q |
9,61 |
4,76 |
9,997 |
1998/ |
1,7 |
4,53 |
5,533 |
1974/Q |
12,7 |
5,13 |
9,323 |
1998/ |
2,1 |
4,43 |
4,860 |
1974/Q |
9,91 |
5,20 |
11,250 |
1999/Q |
0,9 |
4,30 |
4,733 |
1974/Q |
12,8 |
5,63 |
12,090 |
1999/ |
3,1 |
4,26 |
4,747 |
1974/Q |
10,1 |
6,60 |
9,347 |
1999/ |
4,0 |
4,23 |
5,093 |
1975/Q |
6,87 |
8,26 |
6,303 |
1999/ |
2,3 |
4,06 |
5,307 |
1975/Q |
5,26 |
8,86 |
5,420 |
2000/Q |
5,1 |
4,03 |
5,677 |
1975/Q |
8,141 |
8,46 |
6,160 |
2000/ |
3,0 |
3,96 |
6,273 |
1975/Q |
7,26 |
8,30 |
5,413 |
2000/ |
3,0 |
4,06 |
6,520 |
1976/Q |
2,86 |
7,73 |
4,827 |
2000/ |
2,2 |
3,93 |
6,473 |
1976/Q |
4,96 |
7,56 |
5,197 |
2001/Q |
3,1 |
4,16 |
5,593 |
1976/Q |
6,29 |
7,73 |
5,283 |
2001/ |
4,2 |
4,46 |
4,327 |
1976/Q |
5,51 |
7,76 |
4,873 |
2001/ |
0,4 |
4,83 |
3,497 |
1977/Q |
8,13 |
7,50 |
4,660 |
2001/ |
- |
5,60 |
2,133 |
1977/Q |
5,99 |
7,13 |
5,157 |
2002/Q |
2,6 |
5,63 |
1,733 |
1977/Q |
5,25 |
6,90 |
5,820 |
2002/ |
2,9 |
5,83 |
1,750 |
1977/Q |
6,47 |
6,66 |
6,513 |
2002/ |
2,4 |
5,76 |
1,740 |
1978/Q |
7,001 |
6,33 |
6,757 |
2002/ |
1,5 |
5,90 |
1,443 |
1978/Q |
9,96 |
6,00 |
7,283 |
2003/Q |
5,0 |
5,76 |
1,250 |
1978/Q |
9,12 |
6,03 |
8,100 |
2003/ |
- |
6,16 |
1,247 |
1978/Q |
8,33 |
5,90 |
9,583 |
2003/ |
3,0 |
6,13 |
1,017 |
1979/Q |
11,6 |
5,86 |
10,073 |
|
|
|
|
Джерело: The Federal Reserve Bank of St. Louis, database FRED II, http://research.stlouisfed.org/fred2): подано макроекономічні показники для США (щоквартальні дані)
238

Розділ 10. Коінтеграція і векторна модель корекції похибок
10.1. Поняття про коінтеграцію
Дослідження в царині емпіричної макроекономіки майже завжди містять інтегровані й трендові змінні, такі, як дохід, споживання, попит на гроші, рівень цін, зовнішньоторговельні потоки й обмінні курси. Набутий досвід і висновки попередніх підрозділів свідчать про те, що належний спосіб дослідження таких рядів – використати перехід до різниць та інші перетворення (такі, як сезонні коригування) з метою одержати стаціонарні ряди, для аналізу яких можна застосувати VAR-моделі або методи Дж. Бокса і Дж. Дженкінса. Проте нещодавні дослідження та дедалі більший обсяг літератури свідчать про наявність цікавіших і зручніших способів аналізу нестаціонарних змінних.
У цілковито специфікованій моделі регресії |
|
yt xt t |
(10.1) |
є обов'язкове припущення про те, що збурення t є стаціонарним рядом білого шуму11. Однак це припущення навряд чи виявиться правильним за умови, що yt і хt є інтегрованими рядами. Загалом якщо два ряди інтегровані і мають різні порядки інтегрування, то порядок інтегрування їхніх лінійних комбінацій дорівнюватиме вищому з двох порядків. Таким чином, якщо уt і xt є І(1), тобто обидві змінні характеризуються стохастичним трендом, то зазвичай можна очікувати, що yt xt незалежно від значення
, виявиться І(1), а не І(0) (тобто не буде стаціонарною). Якщо й уь, і xt дрейфують, кожна
маючи свій власний тренд, то за умови, що ці тренди не є взаємозв'язаними, різниця між двома змінними також буде характеризуватись своїм власним (стохастичним) трендом. З іншого боку, якщо обидва ряди становлять І(1), то може існувати таке значення , за
якого t yt xt становить I(0). У такому разі з властивостей стаціонарних процесів
випливає, що ця часткова різниця між змінними має зберігатися стабільною навколо фіксованого середнього значення. У результаті ряди дрейфують узгоджено. Два ряди, що
задовольняють цю вимогу, називаються коінтегрованими, а вектор [1, ]T (чи будь-який
паралельний з ним вектор) є коінтеграційним вектором. Модель (10.1) називається в цьому разі коінтеграційною регресією. Підсумуємо сказане у вигляді визначення.
Визначення. Дві І(1)-змінні уь і xt називаються коінтегрованими, якщо існують ненульові числа 1 і 2 , такі, що лінійна комбінація 1xt 2yt є І(0)-процесом. Вектор
[ 1, 2 ]T називається коінтеграційним вектором.
Зауважимо, що у випадку двох змінних коінтеграційні вектори визначені з точністю до
коефіцієнта пропорційності: якщо β [ 1, 2 ]T є коінтеграційним вектором, то вектор β
також буде коінтеграційним для будь якого числа |
0 . Натомість якщо ввести певне |
|||||||||
нормування, наприклад вибрати такий множник |
, щоб 1 1 , як у коінтеграційній |
|||||||||
регресії (10.1), то коінтеграційний вектор буде визначений однозначно. |
|
|||||||||
|
|
Поняття |
коінтеграції можна |
узагальнити |
на випадок довільної |
кількості змінних |
||||
y |
t |
[y |
, ,y |
t,k |
]T |
. У цьому разі |
відповідний |
коінтеграційний вектор |
буде k-вимірним: |
|
|
t1 |
|
|
|
|
|
|
|
||
β [ 1, , k ]T .
Коінтегрованість змінних означає існування довгострокової динамічної рівноваги. Незважаючи на відсутність лагів у регресії, коефіцієнт у рівнянні (10.1) описує саме
довгострокове співвідношення і є, по суті, довгостроковим мультиплікатором12. У такому
11Якщо в моделі й була автокореляція, її усунуто шляхом належної трансформації.
12Корисно порівняти регресію (10.1) для стаціонарних та інтегрованих змінних. У випадку стаціонарних змінних це рівняння за формою описує одночасну залежність. Якщо натомість
фактична залежність є лаговою, то оцінка буде зміщеною. Вона неявно враховує вплив пропущених лагових змінних і насправді оцінює суміш миттєвого та рівноважного мультиплікаторів. У випадку інтегрованих змінних ситуація докорінно змінюється. Якщо змінні не є коінтегрованими, то регресія (10.1) узагалі некоректна. Для коінтегрованих змінних завжди є
239

випадку можна розмежувати довгострокові зв'язки між уt і xt, тобто спосіб, яким обидві ці змінні узгоджено дрейфують, і короткострокову динаміку, тобто зв'язок між відхиленнями yt від його довгострокового тренда та відхиленнями xt від його довгострокового тренда. У цій ситуації перехід до різниць змінних буде непродуктивним, оскільки в моделі не буде враховано довгостроковий зв'язок між yt і xt.. Дослідження коінтеграції та споріднена методологія корекції похибок спрямовано на розробляння методів оцінювання, які дозволяють здобути інформацію про обидві форми залежності13.
Приклад 10.1. Гіпотеза паритету купівельних спроможностей
Гіпотеза паритету купівельних спроможностей стверджує, що в стані довгострокової рівноваги обмінні курси поступово стиратимуть відмінності між купівельними спроможностями в різних економічних системах. Отже, якщо р0 та р1 є рівнями цін у двох країнах, а Е – обмінний курс двох валют, то в стані рівноваги
t Et p1t , p0t
де – константа.
Рівні цін у будь-яких двох країнах, імовірно, матимуть виражені тренди. Однак з урахуванням короткострокових відхилень від рівноваги, гіпотеза паритету купівельних
спроможностей передбачає, що для |
конкретного |
значення |
β [ln , 1,1]T |
у |
моделі |
lnEt 1 2 ln p1t 3 ln p0t t |
|
|
|
|
|
t ln t становитиме стаціонарний |
ряд, а це |
означає, що |
логарифми |
всіх |
трьох |
змінних у моделі коінтегровані. |
|
|
|
|
|
Приклад 10.2. Моделі теперішньої вартості
Стандартна версія моделі теперішньої вартості передбачає, що ціна акції та дивіденди коінтегровані. Точна форма коінтеграційного співвідношення залежить від того, чи
стаціонарні різниці рівнів чи логарифмів дивідендів [38]. Нехай pt – реальна ціна акції (після виплати дивідендів) у період t , dt – дивіденди в період t , b – постійний реальний
коефіцієнт дисконтування. Формула теперішньої вартості має такий вигляд (див.,
наприклад, [30, с.234]):
|
|
|
|
|
|
p M |
|
] |
. |
|
|
(10.2) |
|||||
|
|
|
|
|
|
[ bid |
|
|
|||||||||
|
|
|
|
|
|
t |
t |
t i |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
Припустимо спочатку, як у роботі |
[35], що різниці dt |
стаціонарні. Тоді |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
p |
b d |
M [ bi (d |
d )]. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t |
|
t i 1 |
t i |
t |
|
|
|
|
||
|
|
|
|
1 b |
|
|
|
|
|
||||||||
Оскільки |
dt i dt |
є стаціонарним для |
будь-якого |
і, то права частина останнього |
|||||||||||||
рівняння є стаціонарним рядом14. |
Звідси випливає, |
що p |
є сумою І(1) – процесу та |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
стаціонарного процесу, а отже, становить І(1). Окрім того, |
|
pt |
та dt коінтегровані з |
||||||||||||||
коінтеграційним вектором |
[1; b /(1 b)]T |
. |
|
|
|
|
|
|
|
|
|
||||||
довгостроковим мультиплікатором незалежно від того, якою є справжня динамічна структура залежності.
13 Див. [53]
14 Дисперсія dt i dt зростає як поліном від і, bi – спадна геометрична прогресія. Отже, ряд з дисперсій збігатиметься.
240

Тепер припустимо, що різниці lndt |
стаціонарні. Розділимо обидві частини формули |
||||||
теперішньої вартості на dt . Маємо |
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
M |
[ bi dt i ] |
. |
(10.3) |
|||
|
d |
||||||
|
|
t |
i 1 |
d |
|
|
|
|
t |
|
|
|
t |
|
|
Міркуючи так само, як у попередньому випадку, неважко зрозуміти, що права частина (10.3) є стаціонарним рядом. Логарифмуємо обидві частини (10.3). Бачимо, що ln pt lndt
також є стаціонарним рядом. Таким чином, ln pt є сумою І(1)-ряду та стаціонарного ряду,
тобто становить І(1), а ln pt та lndt коінтегровані з коінтеграційним вектором [1, 1]T .
На завершення прикладу порівняємо обидва випадки. Перший видається цікавішим, оскільки коінтеграційна регресія дає змогу оцінити коефіцієнт дисконтування. Однак, на жаль, саме другий випадок є більш реалістичним, оскільки темпи росту цін на акції та дивідендів будуть приблизно постійними в довгостроковому періоді.
Припустимо, що модель містить k змінних. У такому випадку принаймні теоретично
може бути більше ніж один коінтеграційний вектор. Наприклад, нехай yt [yt1,yt2,yt3 ]T .
Припустимо, |
що |
y |
t1 |
та |
коінтегровані з коінтеграційним вектором |
β |
[ |
|
, ,0]T |
, |
|||||
|
|
|
|
|
|
|
|
1 |
11 |
|
21 |
|
|||
|
0, |
0, |
а |
y |
та |
y |
коінтегровані з коінтеграційним вектором |
β |
2 |
[0, |
22 |
, ]T |
, |
||
11 |
21 |
|
|
t2 |
|
t3 |
|
|
|
|
|
32 |
|
||
22 |
0, 32 |
0 . Ми |
ввели тривимірні вектори замість двовимірних, щоб |
підкреслити, що |
|
||||||||||
ми розглядаємо всі три змінні як єдину систему. Наприклад, добуток |
|
|
|
βT y |
t |
можна |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
розписати покоординатно, як β1T yt 11yt1 21yt2 , отже, становить лінійну комбінацію векторів yt1 та yt2 , як того й вимагає визначення коінтегрованості цих двох змінних. Неважко побачити, що коінтеграційні вектори β1 та β2 лінійно незалежні. Створимо матрицю β розмірністю 3 2, перший стовпчик якої становить вектор β1 (який???), а
другий – β2 (вектори слід писати або прямо жирним, або курсивом із лінією
зверху, але має бути або так, або так по всій роботі). За допомогою цієї матриці можна компактно записати обидва коінтеграційні співвідношення одночасно. Загалом, якщо ми розглядаємо k змінних , між якими існує r лінійно незалежних коінтеграційних
співвідношень, то зручно записувати їх разом як βT yt , де матриця βT має розмірність r k , а її ранг становить r . Елемент ij цієї матриці є коефіцієнтом при змінній yt, j в j -
му коінтеграційному векторі. У системі з k змінних може існувати не більше k 1 лінійно незалежних коінтеграційних векторів. Справді, виходячи з визначення коінтеграції,
запишемо βT yt xt , де xt – векторний І(0)-процес, розмірність якого дорівнює кількості
лінійно незалежних коінтеграційних векторів. Припустимо, що існує k лінійно незалежних коінтеграційних векторів. Тоді матриця β має розмірність k k та ранг k, а отже,
обернену матрицю. Таким чином, yt (βT ) 1xt . Тобто кожний компонент yt виражається
як лінійна комбінація стаціонарних процесів, а отже, є стаціонарним процесом. Одержане протиріччя доводить потрібний нам результат. Кількість лінійно незалежних коінтеграційних векторів, що існують у системі, називається рангом коінтеграції. Ранг коінтеграції може коливатися від 1 до k 1. Нехай r лінійно незалежних коінтеграційних
векторів об'єднані в матрицю βT розмірності r k , тобто βT yt є І(0). Тоді для будь-якої
невиродженої k k -вимірної матриці S розмірністю SβT yt також є І(0)-процесом. На
відміну від випадку існування лише одного коінтеграційного співвідношення, визначення матриці S породжує нетривіальну проблему ідентифікації. Як розв'язати цю проблему на основі моделі корекції похибок, ми розглянемо в підрозд. 10.2
241
Приклад 10.3. Лінійно незалежні коінтеграційні вектори
Модель описує економіку США. Розглянемо систему з п'яти макроекономічних змінних
ytT mt ,inflt ,cprt ,yt ,tbrt T ,
де mt – логарифм грошового агрегату М1 за квартал t; inflt – рівень інфляції за квартал (у річному вимірі); cprt – відсоткова ставка за корпоративними векселями; yt – натуральний
логарифм реального ВВП (мільярди доларів у цінах 1987 р.); tbrt – відсоткова ставка за
векселями державної скарбниці (Tbill).
Уважатимемо, що всі змінні є І(1)-процесами. Апріорі можна очікувати існування трьох коінтеграційних співвідношень. По-перше, можна визначити рівняння попиту на гроші таким чином:
mt 1 41yt 51tbrt t1 ,
де 41 і 51 – коефіцієнти (довгострокової) еластичності стосовно доходу та відсоткової
ставки, відповідно. Можна очікувати, що значення 41 буде близьким до одиниці, а51 0 . По-друге, якщо реальна відсоткова ставка стаціонарна, то рівняння
inflt = μ2 + β52tbrt + εt2
виражає коінтеграційне співвідношення, причому 52 1. Якщо вважати фактичну
інфляцію проксі-змінною для очікуваної інфляції, то останнє рівняння можна інтерпретувати як рівняння Фішера.
Далі можна очікувати, що премія за ризик, вимірювана як різниця між ставками за корпоративними векселями та за векселями державної скарбниці є стаціонарною15. Отже, третє коінтеграційне співвідношення має такий вигляд:
cprt = μ3 + β53tbrt + εt3 .
Ураховуючи, що в системі п'ять змінних, три описані вище коінтеграційні
співвідношення можна записати у вигляді такої матриці: |
|
||||||
|
1 |
0 |
0 |
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|||
|
β |
0 |
0 |
1 |
. |
|
(10.4) |
|
|
41 |
0 |
0 |
|
|
|
|
|
|
|
|
|||
|
|
51 |
52 |
53 |
|
|
|
|
|
|
|
|
|||
10.2. Теорема Грейнджера про зображення і векторна модель корекції похибок
10.2.1. Теорема Грейнджера
Хоча теоретичне підґрунтя моделі становить теорема Грейнджера про зображення, а перший варіант моделі корекції похибок також належить К. Грейнджеру, найбільш уживаним на практиці є підхід С. Йогансена [51,52], розроблений пізніше. Цей підхід дозволяє використати одну і ту саму форму моделі як для діагностики коінтеграції і визначення кількості коінтеграційних співвідношень у моделі з багатьма змінними, так і для оцінювання параметрів у випадку відомої кількості коінтеграційних співвідношень.
Цей підрозділ може видатись перевантаженим технічними деталями, однак, як ми побачимо пізніше, формули, які ми тут розглядатимемо, допоможуть визначити зв'язок між економічною теорією та VEC, а отже, зрозуміти, як здійснювати економічну інтерпретацію оціненої моделі. Векторну модель корекції похибок можна розглядати як векторну авторегресію для коінтегрованих нестаціонарних змінних із певними обмеженнями на параметри моделі. Однак зручніше взяти векторну авторегресію як
15 Ставки за корпоративними та казначейськими векселями розглядають як віддачу (за квартал) на ризикові та безризикові цінні папери, відповідно. Стаціонарність премії за ризик є, у кінцевому підсумку, наслідком припущення про те, що переваги репрезентативного інвестора в системі "ризик – дохід" незмінні в часі.
242
відправну точку та записати модель у дещо іншій формі, яку можна вважати векторним узагальненням регресії Дікі – Фуллера. Отже, розглянемо таку VAR-модель:
|
yt = A1yt-1 +...+ Ap yt- p +Φdt +εt |
, |
(10.5) |
де yt – це k-вимірний вектор |
; εt – збурення; dt – вектор |
детермінованих змінних |
|
(константа, тренди, сезонні фіктивні змінні тощо), наприклад dt μ0 μ1t . Перетворимо модель до такого вигляду:
|
|
p 1 |
|
|
|
|
||
|
|
yt yt 1 |
i yt i dt εt |
, |
(10.6) |
|||
де |
|
i 1 |
|
|
|
|
||
|
p 1 |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Ai , i |
Aj . |
|
|
(10.7) |
||
|
|
i 1 |
|
|
j i 1 |
|
|
|
Зауважимо, що детерміністичні доданки в рівняннях (10.5) і (10.6) однакові. |
|
|||||||
Поведінка yt |
визначається властивостями (матричного) характеристичного полінома, |
|||||||
який можна виразити через коефіцієнти моделі у формі (10.6) таким чином: |
|
|||||||
|
|
(z) (1 z)I |
|
|
p 1 |
zi . |
|
|
|
|
k |
z (1 z) |
|
||||
|
|
|
|
i 1 |
i |
|
||
|
|
|
|
|
|
|
|
|
Визначник П(z) є поліномом степені не вище ніж pk. |
|
|
|
|||||
Якщо модулі |
всіх коренів полінома det(П(z)) |
більше |
ніж одиниця, то yt |
є тренд- |
||||
стаціонарним або стаціонарним залежно від властивостей детермінованих компонентів моделі.
Якщо det(П(z)) має одиничний корінь, то матриця (1) сингулярна, а yt
нестаціонарний. Позначимо її ранг через r , r k . Нехай βT - матриця розмірністю r k ,
яка складається з r лінійно незалежних рядків П, α – матриця розмірністю k r , яка складається з коефіцієнтів, які виражають кожний рядок П як лінійну комбінацію
векторів з набору βT . Отже, αβT . Рівняння (10.6) набуває такого вигляду:
p 1
yt αβ yt 1 i yt i dt εt . (10.8)
i 1
Останнє рівняння описує векторну модель корекції похибок (VEC від vector error correction). Нерідко модель формулюють у вигляді (10.6), але в цьому разі слід обов'язково вказувати, що матриця П має неповний ранг.
Сформулюємо умову, яка гарантує, що процес, який задовольняє рівняння (10.8) є І(1).
p 1
Уведемо такі позначення: Ik i ; α – ортогональне доповнення до α (точніше,
i 1
рядки α становлять базис ортогонального доповнення в Rk до рядків α як k-вимірних векторів).
Умова І(1). Нехай із рівності det( (z)) 0 випливає, |
що |z | 1, або |
z 1. Припустимо |
також, що |
|
|
det αT β 0. |
|
(10.9) |
Зауважимо, що для моделі з одним лагом умова (10.9) набуває особливо зручного
вигляду, тобто власні значення матриці Ir αβT мають бути менше ніж одиниця за
модулем.
Ця умова необхідна для виключення сезонних одиничних коренів, вибухових коренів і процесів, що мають вищі порядки інтегрованості.
Теорема Грейнджера про зображення. |
Процес |
yt (10.8) має таке авторегресійне |
|||||||||
зображення: |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
t |
(ε |
|
|
d |
|
) a |
, |
(10.10) |
|
t |
C |
d ) C (ε |
t i |
|||||||
|
|
i 1 |
t |
t |
i t i |
|
|
|
|
||
|
|
|
|
|
i 0 |
|
|
|
|
|
|
243
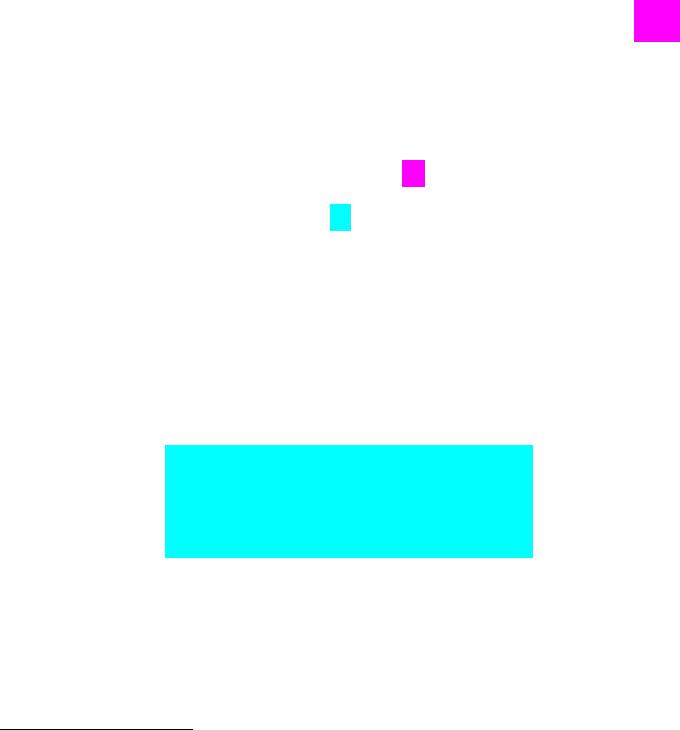
|
C β (αT β ) 1αT |
|
|
|
|
|
|
|
|||||
де |
, а ряд матричних коефіцієнтів16 |
Ci |
збігається достатньо швидко, |
||||||||||
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
щоб ряд |
|
|
утворював стаціонарний процес. |
Вектор a |
визначено початковими |
||||||||
C ε |
|
||||||||||||
|
|
|
i t i |
|
|
|
|
|
|
|
|
|
|
|
|
i 0 |
|
yt становить І(1). Він |
має r лінійно |
|
|
|
|||||
умовами. |
Процес |
|
незалежних коінтеграційних |
||||||||||
векторів |
β |
і p r |
спільних стохастичних трендів |
|
t |
ε |
. |
|
|||||
CT αT |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
Також |
доцільно |
|
визначити матрицю |
L β (αT β ) 1 |
, |
яка |
називається матрицею |
||||||
t
навантаження (англ. loadings matrix). Таким чином, стохастичний тренд C εi
i 1
розбивається на спільні тренди, які є рушійними силами системи, і матрицю навантаження.
Теорема Грейнджера про зображення обґрунтовує модель корекції похибок (10.8). Окрім того, вона допомагає проінтерпретувати цю модель.
10.2.2. Коінтеграційні вектори
Із теореми Грейнджера випливає, що матриця βT , (будь ласка, перевірте всі
формули, зокрема матриці та вектори: вони то жирні, то ні, то прямо, то курсивом!!! Загалом треба писати T ) яка фігурує в рівнянні моделі (10.8) є
матрицею коінтеграційних співвідношень. Для будь-якої несингулярної матриці S вираз
SβT yt |
також |
задає |
r |
лінійно |
незалежних |
коінтеграційних |
співвідношень, |
а |
|||||||||
αβT (αS-1 )(SβT ). |
Отже, |
незважаючи |
на те, |
що |
П фіксована, |
α та |
βT |
визначені |
|||||||||
неоднозначно. Згадаймо, що матриця |
βT |
|
має таку структуру: вона складається з r рядків |
||||||||||||||
та k |
стовпчиків, i -й |
рядок відповідає |
i -му коінтеграційному співвідношенню, |
j -й |
|||||||||||||
кожний стовпчик складається з коефіцієнтів |
при |
j -й змінній |
моделі |
в кожному |
|||||||||||||
|
|
||||||||||||||||
коінтеграційному співвідношенні. Для визначення (ідентифікації) |
βT |
|
найчастіше |
||||||||||||||
використовують |
таке |
нормування: |
j |
стовпчиків |
цієї матриці |
перетворюються |
на |
||||||||||
одиничну матрицю. У системі з п'яти змінних, розглянутій у прикл. 10.3, за умови, що ранг коінтеграції дорівнює трьом, ідентифікуюче нормування може бути таким17:
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|||
|
0 |
1 |
0 |
|
1 0 |
0 |
41 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
51 |
. |
|
|
β |
0 |
0 |
1 |
, βT |
0 1 |
0 |
|
42 |
|
(10.11) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
52 |
|
|
|
|
|
|
|
|
|
|
0 0 |
1 |
|
|
|
|
|
||
|
41 |
42 |
43 |
|
43 |
|
|||||||||
|
|
|
|
|
|
|
53 |
|
|
||||||
|
51 |
52 |
53 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
Зауважимо, що матрицю (10.4), виведену з міркувань економічної теорії, можна одержати з матриці (10.11) при обмеженнях 42 0 , 43 0 . Таким чином, матриця (10.4)
дає приклад надідентифікуючих обмежень. Щоб статистично коректно оцінити коінтеграційні співвідношення (10.11) на основі VEC (10.8), слід перевірити гіпотезу про те, що ранг коінтеграції в системі дорівнює трьом. Ми дізнаємось, як це зробити, трохи пізніше. Припустимо, що гіпотезу про ранг не буде відхилено. Коінтеграційні співвідношення (10.4) ми вивели з міркувань економічної теорії. Щоб переконатись у тому, що ці співвідношення статистично обґрунтовані, треба спочатку оцінити VEC за умови, що ранг коінтеграції дорівнює трьом, використавши нормування (10.11), а потім в
16Матриці Ci слід визначати на основі розкладу в степеневий ряд виразу (1 z) 1(z) , де z – комплексна
змінна.
17зрозуміло, що ми можемо вибрати три змінні з п’яти C53 способами.
244
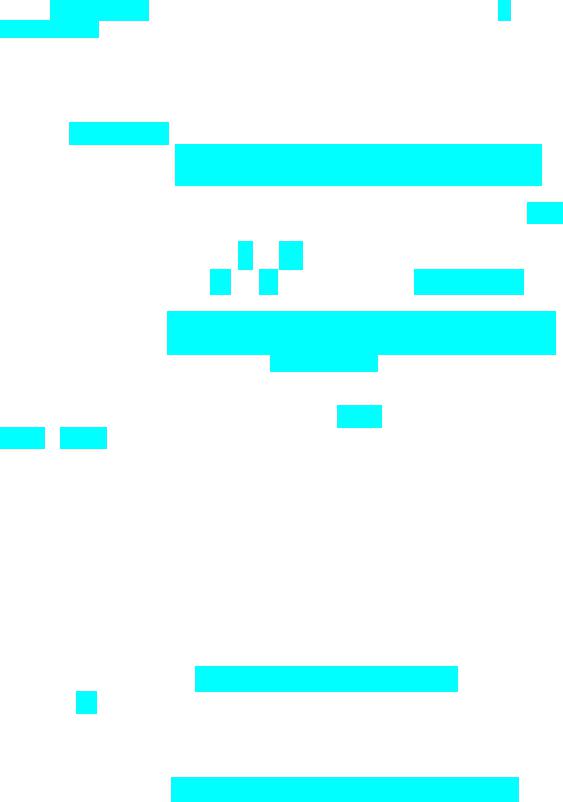
оціненій моделі перевірити гіпотезу 42 0 , 43 0 . Аналізуючи друге співвідношення з прикл. 10.3, ми припускали, що 52 1. У цьому разі остаточний варіант гіпотези складається з трьох обмежень: 42 0 ; 43 0 ; 52 1. Перевірку подібних гіпотез ми
розглянемо далі.
Зазначимо, що вибравши одне ідентифікуюче нормування, ми можемо перейти до будь-якого іншого допустимого. Цим фактом ми скористаємось, коли будемо розглядати метод С. Йогансена для оцінювання моделі (тобто маючи оцінку β за умови нормування
С. Йогансена, ми відразу можемо знайти, скажімо, оцінку за умови нормування, описаної кількома рядками вище).
10.2.3. Роль детермінованих змінних у поведінці системи
Наслідуючи C. Йогансена [52], розглянемо кілька спеціальних випадків . Нехай dt μ0 μ1t . Тоді рівняння (10.10) набуде такого вигляду:
t |
|
μ1(t i)) a . |
|
yt C (εt μ0 |
μ1t) Ci *(εt i μ0 |
(10.12) |
|
i 1 |
i 0 |
|
|
З рівняння (10.12) випливає, що в загальному випадку наявність константи в моделі корекції похибок (10.8) означає, що в даних існує лінійний тренд Ctμ0 , а з наявності
лінійного тренда в (10.8) випливає, що дані характеризуються квадратичним трендом
12 Ct2 . Оскільки рядки матриць та як вектори утворюють базис у Rk , то ми можемо
записати розклад векторів μ0 та μ1 за цим базисом: μi iT iT , i 0,1 . Тоді модель (10.8) можна записати таким чином:
p 1
yt α(βT yt 1 ρ0T ρ1Tt) i yt i α (γ0T γ1Tt) εt . (10.13).
i 1
Тобто детерміновані доданки слід поділити на дві частини. Одна входить до коінтеграційних співвідношень таким чином, щоб математичне сподівання в цих співвідношеннях дорівнювало нулю. Друга існує у вигляді окремих доданків в моделі корекції похибок. Можна показати, що коли 1 0 , то квадратичний тренд зникає, а коли
μ1 0 , 0 0 , то зникає лінійний тренд. Зауважимо, що саме зображення (10.13)
найчастіше використовують під час практичного оцінювання моделей у більшій частині економетричного програмного забезпечення. Будемо розрізняти такі п'ять випадків моделі (10.8):
1. Дані |
yt |
не мають детермінованого |
|
тренда, |
|
а |
коінтеграційні співвідношення не |
|||||||||||||||||
містять константи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
αβT y |
t 1 |
d |
αβT y |
t 1 |
|
|
|
(10.14) |
||||||||
2. Дані |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
коінтеграційні співвідношення мають |
|||||||
yt |
|
не мають детермінованого тренда, а |
||||||||||||||||||||||
константи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αβT y |
t 1 |
d |
α(βT y |
t 1 |
ρT ) |
. |
(10.15) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
0 |
|
|
|
||||
3. Дані |
|
yt |
мають лінійний |
тренд, а |
|
коінтеграційні співвідношення |
мають лише |
|||||||||||||||||
константи: |
|
|
|
αβT y |
t 1 |
d |
α(βT y |
t 1 |
ρT ) α |
γT . |
(10.16) |
|||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
0 |
|
0 |
|
|||||
4. Дані yt і коінтеграційні співвідношення мають лінійний тренд:
|
|
|
αβT y |
t 1 |
d |
α(βT y |
t 1 |
ρT ρTt) α |
|
(γT γTt) |
|
(10.17) |
|||
5. Дані |
|
мають |
|
t |
|
|
0 |
1 |
0 |
1 |
|
|
|||
yt |
квадратичний |
тренд, а |
коінтеграційні |
співвідношення |
мають |
||||||||||
лінійний тренд |
: |
|
|
|
|
|
|
|
|
|
|
|
|
||
αβT y |
t 1 |
d |
α(βT y |
t 1 |
ρT ρTt) α |
|
(γT γTt) |
(10.18) |
|
t |
|
0 1 |
0 1 |
|
П'ять описаних випадків ситуації враховано в більшій частині економетричних програм. Отже, беручи до уваги поведінку наявних даних, перш ніж діагностувати коінтеграцію й оцінювати модель корекції похибок, слід визначити, яку форму моделі
245

треба обрати. Оскільки економічні змінні зазвичай додатні, то перша ситуація майже ніколи не зустрічається. Ситуація 5 (квадратичний тренд у даних) виникає також досить нечасто. Отже, форму моделі 2 застосовують, коли дані не містять явного тренда. Випадки 3 і 4 придатні в ситуації, коли дані містять лінійний тренд. Зазвичай починають з п. 3, а якщо немає коінтеграції, переходять до п. 4.
10.2.4. Функція імпульсної реакції
Зображення (10.10) дає можливість визначити функцію імпульсної реакції: реакція компонентів yt h на шоки εt виражається як елементи матриці C Ch * . Із теореми
Грейнджера про зображення випливає, що Ch * 0 при h . Тому, на відміну від
векторної авторегресії для стаціонарних змінних, граничні значення функцій імпульсної реакції не обов'язково є нулями: їх задають відповідні елементи матриці С. Зауважимо, що матриці С та Ch * визначено матрицями П та Гі і не залежать від нормування α та
β .
Спільні стохастичні тренди ми детальніше проаналізуємо в п. 10.2.5.
10.2.5. Економічна теорія та VEC.
Деякі корисні факти про VEC-форму VAR(1). Векторну авторегресію першого порядку без тренда і з обмеженою константою (10.15) можна перетворити до VEC такого вигляду:
|
y |
t |
α(βT y |
t 1 |
ρ |
0 |
) ε |
. |
(10.19) |
|
|
|
|
t |
|
|
|||
У цьому випадку умова І(1) така: власні значення матриці Ir αβT |
мають бути менше |
||||||||
ніж одиниця за модулем, де r , як і раніше, є рангом коінтеграції. Зображення Грейнджера буде таким:
|
|
|
|
y |
|
|
t |
|
|
|
*(ε |
αρT ) Cy |
|
, |
(10.20) |
||||||
|
|
|
|
t |
C |
ε C |
i |
0 |
|||||||||||||
|
|
|
|
|
|
i 1 |
t |
|
|
|
t i |
|
|
0 |
|
|
|||||
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
де |
C β (αTβ ) 1αT |
, |
Ci * α(αTβ ) 1(Ir |
βTα)i βT |
. |
|
|
|
|
|
|
|
|
||||||||
|
Для зручності наведемо разом основні конструкції. |
|
|
|
|||||||||||||||||
Функції імпульсної реакції визначено елементами матриці |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
M(yt h |yt ) C C |
h |
* |
, |
|
|
(10.21) |
||||||||
|
|
|
|
|
|
|
|
|
εt |
|
|
|
|
|
|
|
|
|
|
|
|
де Ch * 0 при h . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рушійними силами системи є k r |
спільних стохастичних трендів: |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
CT αT |
t |
|
ε |
. |
|
|
|
|
|
|
(10.22) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
i 1 |
|
i |
|
|
|
|
|
|
|
|
|
Множина атракторів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
A {y Rk |βT y ρ0T } |
|
|
(10.23) |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
описує можливі набори значень змінних, при яких досягається стан динамічної рівноваги.
Матриця навантажень |
|
L β (αT β ) 1. |
(10.24) |
Вона показує, як саме кожний з k r спільних стохастичних трендів діє на окремі змінні системи.
Проста статична теоретична модель. Розглянемо просту, але типову економічну модель. З одного боку, вона проста, тому що статична, тобто описує одночасні залежності між змінними, і складається лише з чотирьох змінних: двох ендогенних і двох екзогенних. З іншого боку, вона типова, оскільки велика кількість економічних моделей має аналогічну базову структуру, або алгебраїчне зображення. У цьому розумінні прикладами можуть бути стандартний аналіз попиту та пропозиції на певному ринку, статичні моделі IS-LM та AS-AD або, скажімо, більш сучасна модель формування заробітної плати на
246
