
Zolotaryuk_lectures
.pdfÒ îðiÿ ñîëiòîíi .
теоретично¨Д. .-м. . Я.O. Золотарюк
Iнститут iзики iм. М.М. Боголюбова НАН Укра¨ни
ì. Êè¨â 31.14.2010
2
Çìiñò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
Вступ |
|
|
|
|
|
|
|
|
|
|
|
|
|
та дисперсi¨. |
|
5 |
|||||
|
1.1 |
Конуруючi е екти |
|
|
|
|
|
|||||||||||||||
|
|
1.1.3 |
|
E åкти нелвластивостiнелiнiйностi. . . . . . . . . . . . . . . . . . . . |
8 |
|||||||||||||||||
|
|
|
|
1 |
|
Загальнi |
|
|
|
|
рiвнянь першого порядку |
6 |
||||||||||
2 |
|
|
|
2 |
|
iп рболiчнi неди пергуючi хвилi |
|
|
7 |
|||||||||||||
Оберненат його розв'язкидача |
|
|
|
|
ля рiвняння Koртевега-де Фрiза |
11 |
||||||||||||||||
|
1 |
Õâèëi |
|
|
|
âîäi, |
розсiяннярiвнян К Ф . . . . . . |
|
|
|||||||||||||
|
2 |
Ê |
3 |
|
|
Фазова |
площина |
|
|
|
|
КдФПастйого розв'язки |
|
5 |
||||||||
|
|
íòèíó |
|
|
|
|
границя |
задачi Фермi- |
а-Улама. |
|
||||||||||||
|
3 |
озв'язкильнавл стивостi |
|
äëÿ |
рiвняння KдФ |
18 |
||||||||||||||||
|
2.4 |
Обернена задача |
|
|
|
|||||||||||||||||
|
|
|
|
1 |
|
Iнт грали |
уху рiвняння КдФ |
|
|
|
2 |
|||||||||||
|
|
|
|
2 |
|
|
еретворен |
Ìióðè |
|
|
|
|
|
|
3 |
|||||||
|
|
|
|
3 |
|
|
|
едставлеозсiянняЛакса . . |
|
|
|
|
|
5 |
||||||||
|
|
|
|
4 |
|
Ïðяма задача розсiяння |
|
|
|
|
26 |
|||||||||||
|
|
|
|
5 |
|
Залежнiсть даних розсiяння вiд часу. iвняння КМ. |
|
1 |
||||||||||||||
|
|
|
4 |
6 |
|
iвняння ель анда-Левiтана-Марченк |
|
2 |
||||||||||||||
|
|
|
7 |
|
3адача урси . . . . . . . . |
|
|
|
|
3 |
||||||||||||
|
2.5 |
|
|
1 |
|
|
|
|
|
|
|
|
потенцiали. Детермiнантна ормула |
|
5 |
|||||||
|
Солiтоннi розв'язки рiвняння КдФ. |
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
НевiдбиваючiОднос |
|
|
ç |
|
|
|
|
|
|
7 |
||||||
|
|
|
|
3 |
|
Двохсолiтонний |
|
â'ÿçîê |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
09 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3653 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
5.432154 |
зв'язкизадачатоноваПовнаЗв'язок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.àìiëü |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
тОбернена2.6 ¨хнi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
Знах дження елементарних розв'язкiв рiвн |
Ñ€ |
|
4 |
|||||||||||||||||
|
2 |
Побудова |
|
îìóò |
|
|
|
представлення |
ë |
рiвняння синус- |
60 |
|||||||||||
|
3.3 |
Обернена |
задачаацiйногорiвнянняр зсiяння дл |
системи |
äâîõ Ä . . . . . . . . |
|||||||||||||||||
|
|
ордон т |
|
íåëiíiéí |
|
|
|
3 |
Шредiнгера . . . |
|
8 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
54
6
7
|
|
1 |
|
|
|
задачi |
|
|
|
|
ÇÌIÑÒ |
|||
|
|
|
|
ðîçñiÿííÿ |
|
падкiв нелiнiйного |
4 |
|||||||
|
|
2 |
Залеж iсть |
|
âiä ÷àñó |
|
|
|||||||
|
|
3 |
Виедукцi¨детермiнa |
тних ормудля(явного зв'язку мiж |
|
|
2 |
|||||||
|
|
|
ðiâíÿí |
|
Øðåäi ãåðà (Í Ø) à èнусордон (С ). |
|
|
|||||||
|
|
|
íèìè |
ðîçñiÿííÿ |
ò |
потенцiалом). iвняння €ель анäà- |
5 |
|||||||
|
3 4 |
Левiтана-Марчеданихка. |
|
|
|
|
|
|||||||
|
3aäà÷a óðñè . . . . . . . |
|
|
|
|
|
7 |
|||||||
3..154 Механiчнi3ОсновнiПобудова.54.321застосуванняДвохБризериСолiтонозв'язоксмоделiБеклунда-солiтоннiрiв.щорозв'зки.íiрiвняння.оготисолiтонянняописуютьсрозв'язки. .розв'язку.зв'язаних€рiвняння.ЛМ. .С.рiвнянням.рiвняння.Ñ. . . . .ÑÑ. . . . . . . . . . |
74321 |
|||||||||||||
68 |
||||||||||||||
79 |
||||||||||||||
5ФiзичнiПеретворенняN |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
iвняння С як континуальна границя атомного лан- |
|
||||||||||
|
|
1 |
öþæê . . . . . . . . . . . . |
|
|
|
|
1 |
||||||
|
1 |
Ñòàöiîíàð èé |
|
åêò Äæ |
ñîíà |
|
|
|||||||
|
2 |
Модель ланцюжк |
|
маятникiв |
|
|
0 |
|||||||
5.2 |
|
Ê íò |
|
|
Джозе сона як |
лiнiйна динамiчна система |
4 |
|||||||
iвняння С |
|
å åêò Äæ |
|
. |
|
|
|
5 |
||||||
|
|
3 |
Ä âãèé |
онтакт Джозе сона |
|
довгому конактi Дж |
|
- |
||||||
|
|
4 |
лектромагнiтнi |
збудження |
|
|
87 |
|||||||
|
5.2.5 |
ñîíà. . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
|
|||||||||||
|
Å екти дисипацi¨ для довгого контакта Джозе сона |
|
1 |
|||||||||||
Теорiя збуре |
|
|
|
|
|
|
|
|
|
|
99 |
|||
1 |
Ìåòî |
зовнiшнього струму . . . . . . . . . . . . . |
|
|
||||||||||
|
|
у енергi¨. . . . . . . . . . . . . . . . . |
|
|
3 |
|||||||||
2 |
Ñòàíäàðò à ñõ |
багат солiтонно¨ теорi¨ збурень |
|
|
5 |
|||||||||
|
|
1 |
Ди амiкемасонадиничного люксона пiд дi¹ю постiйного |
7 |
||||||||||
6.3 Динамiкбал люк |
â |
|
вгому |
онтактi Джозе сона |
|
|
||||||||
|
6.3.2 |
Вза¹модiя люксо з мiкрозакоротками . . . . . . . . |
103 |
|||||||||||
Нелiнiйне рiвняння Шредiнгера |
|
|
|
|
|
|||||||||
îçäië 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Вступ |
|
даного курсу лекцiй можна знайти |
книжках [1, |
||||||||||||||
Iн ормацiю з |
|
|
|||||||||||||||
òîì |
|
тематикирпнi 1834 року пiд час проведення ек |
|
|
äëÿ |
||||||||||||
проектування |
áàðæ |
àíàëi Þ iîí |
|
|
Единбурга. Оñьпериментiвщо писа ас |
||||||||||||
2, 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Солiтон вперше спостерiгався британським дослiдником Джоном Скот |
|||||||||||||||
сел з приасселом |
|
ого спостереж |
íÿ: |
|
|
|
|
âå |
швидкiстю, |
||||||||
..., потiм вiдiрвалося вiд нь |
пок тилася вперед |
||||||||||||||||
|
áó øè |
вигляду ве |
óñ |
|
|
поблизудвищення; |
|
гладкий, чi- |
|||||||||
òêî |
âираже ий горб води продамiтненогожував свiй рух вздовж кана |
áåç |
|
|
|||||||||||||
íà êîíi i |
догнав |
¨¨, ликогоона все ще рухал ся зi |
|
ликоюб изько восьверхи |
|||||||||||||
змiни орми або зменше ня швидкостi. Я кину ся |
цi¹ю хвилею |
|
|
||||||||||||||
â |
|
àòèâ ¨¨ íà |
згинах каналу. Так |
|
серпнi мiсяцi 1834округлий,. вiдбуласявидимо¨ |
||||||||||||
àáî |
|
åâ'ÿòè ìèëü |
годину, |
|
é âiä óòà |
|
швидкiстюу орм |
мала лизько |
|||||||||
|
|
|
|
íòiâ |
довжину |
пiвторза тiв |
âèñî |
|
ó. ˆ¨ |
||||||||
|
исота постóпово зменшувалась,зберiгаючипiсляпочаткоäíi¹¨ àáî äâîõ ìèëü ãîíèò |
|
|||||||||||||||
тридцятиназвав Хвилею Переносу... |
|
|
|
|
|
|
|
|
|
||||||||
перша випадкова зустрiч з цим незвичайним та прекрасним явищем, ÿêå |
|||||||||||||||||
1.1 |
Конуруючi е екти нелiнiйностi |
диспер- |
|||||||||||||||
озглянемо загальне лiнiйне ди еренцiальне рiвняння в частинних |
ïîõi- |
||||||||||||||||
|
|
|
ñi¨. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íèõ íà óíêöiþ u = u(x, t): |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
(1.1) |
|
äå |
|
|
|
|
|
|
|
L[u] = 0 , |
|
|
|
|
|||||
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
я .длямеЗа- |
||
|
|
|
|
|
|
|
àстивостейнеоператоррiвяннядисперсiйнможназпостiйнимизв'язугоспiввiдношенкоеатиiцi¹нтарiзниìè |
||||||||||
лiнiйнтонаявностiдамиL - .хлiнiйнийВхвильпочатковихзалежностiдиеренцiйнийумоввiдилi |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
ω = ω(k), xâ |
ìîæí |
класи i увати наступним чиíîì: 1 |
|||||||||
|
|
• |
кiстьДиспергуючiне¹сталоюхвилiдлякщовсiхω′′(k) = 0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значень . В |
акому випадку азова швид |
|||||||
альнi1Цядлякласизада iкацiяданогонеспецкурсувичерпу¹. |
можливi5 типиk. Toмухвиль, початклише овийвизнача¹iмпульстипи, актуроз- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

6 |
|
|
|
|
ОЗДIЛ 1. ВСТУП |
|||
|
|
плива¹ться у просторi, розпадаючись на хвилi рiзно¨ довжини. Хвилi |
||||||
|
|
з рiзними довжинами мають рiзну азову швидкiсть. Приклади: |
2) |
|||||
|
|
ut + cux − µuxx = 0 |
|
балки, |
|
|||
|
|
µ > 0 , |
ω(k) = ck − iµk2 |
|
||||
|
|
ut + cux + µuxxx = 0 |
µ > 0 , |
ω(k) = ck − µk3, |
|
3 |
||
|
|
utt + µuxxxx = 0 |
µ > 0 , |
ω(k) = ±√ |
µk2 |
|
4 |
|
|
|
2 |
|
|
|
ck |
|
|
|
|
-нянПершелiнiйнеямрiвнянняКортевегарiвняння¹ -лiнiйБусiдеФрiза,íескаимрiвнянням.трет¹ - рiвнянняБюргерса,швидкiстюоливаньдруге ëiíiéнимчеверте(1ðiâ.5)- |
||||||
|
|
utt − c uxx − µuxxxx |
µ > 0 , |
ω(k) = ±p1-+ µk2 . |
|
|
||
|
|
повсюджуютьсНедиспергуючi хвилiзпостiйноюякщо ω′′(k) = 0 |
|
|
|
ðîç- |
||
|
• |
|
|
диспергуючою, |
|
|
||
|
|
|
|
азовою . B |
акому. випадкуПриклади:хвилi |
|
|
|
|
|
|
ut + cux = 0 , |
|
|
|
6) |
|
|
|
|
utt − c2uxx = 0 |
|
|
(1.7 |
||
маозглянемоБюргерса1.1•Слiддисип.1ДисипативнiзЗагальнi.тивназначити,нелiнiйнехвиляхвилi:щовластивостiхвильовевищевкможω(kбутиазанi) рiвняння6= 0.класирiвняньпершогоiкацi¨мопершогопорядку:якжутьлiнiйномуперетинатися,порядкурiвняннiзокре-
|
|
u(x, t |
òà çвернемо увагу на те, що повна |
||||
зглянемо ункцiю на площинi |
|
|
8) |
|
|
(1.8) |
|
ut + c u)ux = 0 |
|||||||
ïîõiäíà u(x, t) по часу ма¹ вигляд: |
(1 8) |
|
|
||||
du |
|
|
dx |
|
|||
Oтже, ираз лiво¨ сторони рiвíÿ |
|
|
(1. |
|
явля¹ собою повну похiдну ункцi¨(1.9) |
||
dt |
=íÿut + ux dt . |
||||||
u(x, t) âздовж криво¨ на площинi (x, t), ÿêà |
к жнiй сво¨й точцi ма¹ нахил |
||||||
dx
Такимпрямихщинi чином,(осклькирозв'язанняправачастинарiðiвняння= c .u .тотожнополяга¹ удорiвню¹вiдшуканунiлю)сiмейства(1пло.10)-
dt
наозглянемоцiй(x,ïðt)ямiйкрiвняння.жнаЦiямiких.8)(1 називаюма¹почанахилòковоюьс c(xapaктеристикамиu),умовоювiдповiдний значенрiвнянняюункцi¨(1.8)u.
u(x, 0) = f (x), −∞ < x < ∞ .
1.1. КОНУ УЮЧI ЕФЕКТИ НЕЛIНIЙНОСТI ТА ДИСПЕ СIˆ. |
7 |
Нexaй на площинi (x, t) ляда¹деяк пряма перетина¹ вiсьдорiвню¹OX òî÷öi x = ξ. Toäi uрiвняння= f (ξ) цi¹¨на всiйкриво¨цiйвигпрямiй, яканахил цi¹¨ прямо¨ c[f (ξ)]. Oòæå
а розв'язок рiвняння можна записуватиx = ξ + c[f (ξÿê)]t,
орму1зглянемо.2 лоювсе iперболiчнiсiмействорiвнянняцих(1.6)кривих.недиспергуючiЗагальний. розв'язокхвилiцього. Величинарiвняння зада¹тьсяпараме- |
|||||||||||
1тризу¹. |
|
|
|
|
|
|
u = f (ξ) |
ξ |
|
||
|
|
u(x, t) = f (x − ct), äå f ¹ довiльною ункцi¹ю. Конкретизу¹мо |
|||||||||
f , взявши наступну початкову умову. |
|
|
|
(1.11) |
|||||||
|
|
|
вигляд розв'язку |
|
|
0 , |
|
÷àñó|x| > a |
|||
Тому явний |
u(x, 0) = f (x) = |
a2 − x2 , |
|
|x| ≤ a |
|||||||
|
|
для ненульового |
|
|
|
||||||
тично: |
|
|
|
|
|
|
|
t запису¹ться автома- |
|||
Öåé |
|
0 , |
|ξ| > a |
|
вiд часузмiню¹0стацiонарним, |x −,ctòîìó| > aùî. iмпульс |
||||||
u(x, t) = |
|
a2 − ξ2 , |
|ξ| ≤ a |
|
= |
a2 − (x |
− ct)2 , |
|x − ct| ≤ a |
(1.12) |
||
|
розв'язок явно не залежить |
|
|
|
|
|
|
||||
fрiвняння(ξ) руха¹ться(1.6)задовiльняютьiз швидкiстю c |
íå |
|
свою орму. Характеристики |
||||||||
|
|
|
|
dx/dt = c. |
|
|
|
|
|||
|
|
(b) |
t |
t |
dx/dt=u |
(a) |
|
|
|
|
|
|
dx/dt=c |
|
|
x |
x |
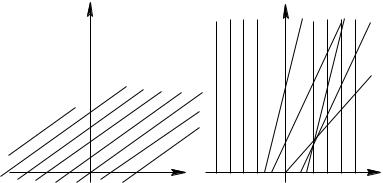
нелiнiйногоис. 1.1: Характеристикирiвняння лiнiйного хвильового рiвняння ut + cux = 0 (a) òà |
||
ut + uux = 0 з початковою умовою (1.11). |
||

8 |
нелiнiйностi |
ОЗДIЛ 1. ВСТУП |
1.1.3 |
|
|
озглянемоE .зв.ектирiвняння Бюргерса без дисперсi¨ |
|
|
нянняозв'яжемома¹вигляд:йогометодом характеристик. Вiдповiдне характристичне(1рiв.13)- |
|||||||
|
ut + uux = 0 . |
|
|||||
|
dt |
dx |
du |
|
|||
отже вздовж характеристики |
викон= ó¹òüñÿ= |
|
вираз, |
(1.14) |
|||
0 |
|||||||
1 |
|
u |
|
|
|||
величи а |
|
dx |
= u , |
(1.15) |
|||
|
|
||||||
|
|
dt |
|
|
|
||
наступíèìuнеявнимзберiга¹тьсячином:iзагальний розв'язок рiвняння (1.13) запису¹ться
= |
2t2 |
− ut) . |
− | ≤ |
(1.17) |
Варто пiдкреслити, що невiдомаu(x, t) óíêöiÿ= f (x |
|
(1.16) |
||
Очевиднавищена еден t > ts |
ts |
÷èòè, |
допустимi обидва знаки у |
|
|
|
u(x, t) входить в аргумент ункцi¨ |
||
ðîçâ'ÿçîêf (ξ). Якщоможнавзятизаписатипочаткову умову (1.11) тa виразити u явним чином, то
|
|
0 |
, |
| | ≤ |
|ξ| > a, − |
|
u(x, t) = |
a2 |
− ξ2 |
, |
ξ |
a, ξ = x |
ut = |
Ïðè ïå íîìó |
|
|
|
||x |
− ut| > a . |
|
|
|
2xt−1±√ |
1−4xt+4a2t2 |
|
x |
ut a , |
|
му виразi,дерозв'язкутойщечасслiдяквизнапри |
|
|
|
||
ктеристик.двîзначнiсть |
, те саме можнавартопобачитибратиз лишеаналiзу хара-. |
|||||
|
|
|
t |
≤ ts |
|
+ |
|
1 |
|
|
|
|
|
|
|
0.9 |
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
0.7 |
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
0.3 |
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
-0. |
|
|
|
|
|
|
ис. 1.2: Поведiнка-1 розв'язку-0.5 нелiнiйного0 |
рiвняння0.5 |
1 |
|
|
|||
вою умовою (1. |
11) |
ïðè |
|
|
ut + uux = 0 з початко- |
||
початкЗчення |
a = 1 умовимоменти часу t = 0.1, 0.3, 0.5. |
|
|
||||
овий моментзначимо |
çìiíè |
ахилу похiдно¨ в точцi |
x = a |
. Â |
|||
ts |
|
|
|
|
|
||
неоднозначною лèøåuxïðè(a, 0) = −2a < 0. Ôóíêöiÿ u(x, t) ïðè x ≥ a ìîæå áóòè |
|||||||
|
|
ux(a, 0) > 0, òîìó |
|
|
|
||

1.1. КОНУ УЮЧI ЕФЕКТИ НЕЛIНIЙНОСТI ТА ДИСПЕ СIˆ. |
9 |
||||||||||
Звiдки елементарно |
( |
|
0 |
|
|
, |
|
x |
ut > a . |
|
|
ux(x, t) = |
|
1 (1−4xt+4a2t2 )−1/2 |
, |
|
|x − ut| ≤ a , |
|
|||||
|
|
t |
|
|
|
|
|||||
|
виплива¹ |
|
|
|
|
|
|
| |
− | |
|
|
çâiäêè |
ux(a, t) = |
|
|
2t |
2 |
|
, |
|
(1.18) |
||
2t2 |
1 − |
2at |
ξ = x − ut . |
||||||||
ux = ∂ξ ∂x = fξ [1 − tux] = ux(x, t) = 1 + tfξ |
, |
(1.19) |
|||||||||
|
|
|
1 |
|
|
|
t |
|
|
|
|
виглядуПопереднi. Введемомiркування. початковiйлегковираз:умовiзширити(1.11)початковийнапочатковiпропроiльiлi загальногоорми |
|||||||||
|
ts = 1/(2a) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
f (x |
Ди еренцiюючи |
èðàç (1.16) |
маючи на увазi ux = uξ , отриму¹мо для. |
|||||||
ïîõiäíî¨ |
|
|
|
||||||
|
ux(a, t) наступний |
|
|
|
|
||||
|
|
∂f ∂ξ |
|
|
|
fξ |
|||
Я що початк |
îâèé ïðî iëü |
|
|
|
|
||||
|
|
|
|
||||||
|
|
|
|
|
f (ξ)мiнiмальному¹вiд'¹мний хил в певнiй точцi ξ, то при |
||||
вц окаволiть перший такий[тобтомоментпри |
ðîñó iëþâ'ÿçîêíàперестмiнiмумуча¹ бути, оскiлькиднознач насим |
||||||||
t > ts = (−1/fξ)min |
|
|
|
(−1/fξ) |
|||||
|
|
|
|
|
|
|
ç óхвилiютьсямови. без змiни ункцi¨орми. Íåëiíié-. |
||
|
|
|
|
|
|
ïовсюдж¹ться |
|
|
|
|
Bиснопризâîдитьк. Лiнiйнiдо де,хвилiормацi¨визнароз÷à |
|
|
−1/fξ(ξ) |
|||||
íiñòü x0 |
= ξ0 +tsf (ξ0) ξ0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
10 |
ОЗДIЛ 1. ВСТУП |
