§3. Плотность распределения вероятностей

Плотностью распределения вероятностейслучайной величины называется производная от функции распределения вероятностей:.

Плотность распределения вероятностей задается только для непрерывной случайной величины. Ее называют также законом распределениянепрерывной случайной величины или дифференциальной функцией распределения. Функцию распределения вероятностей называют интегральной функцией распределения.

Свойства плотности распределения вероятностей:

1. Значение плотности распределения вероятностей неотрицательно, так она является производной от неубывающей функции: .

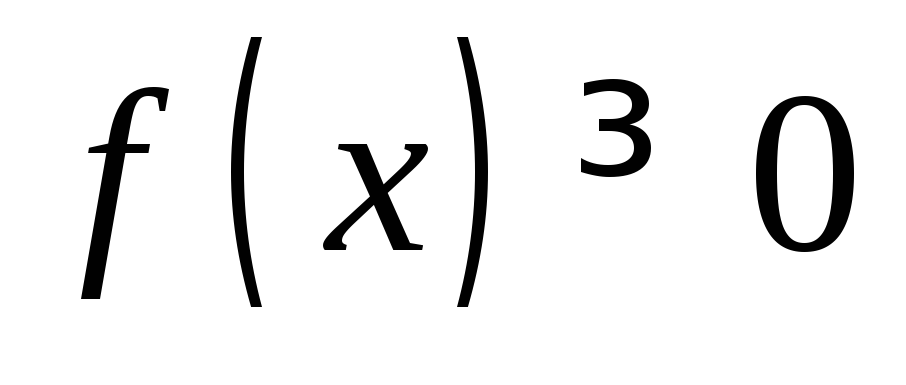2. Вероятность попадания значений случайной величины в интервал (a;b) может быть найдена по формуле:.

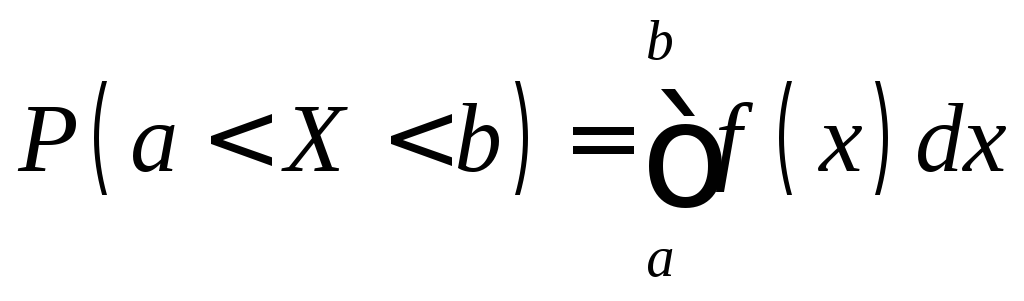3. При известной плотности распределения вероятностей функция распределения может быть найдена по формуле: .

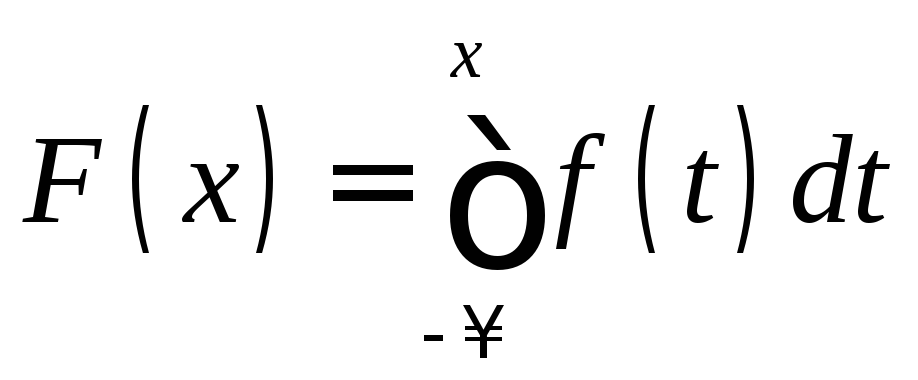4. Условие нормировки: .

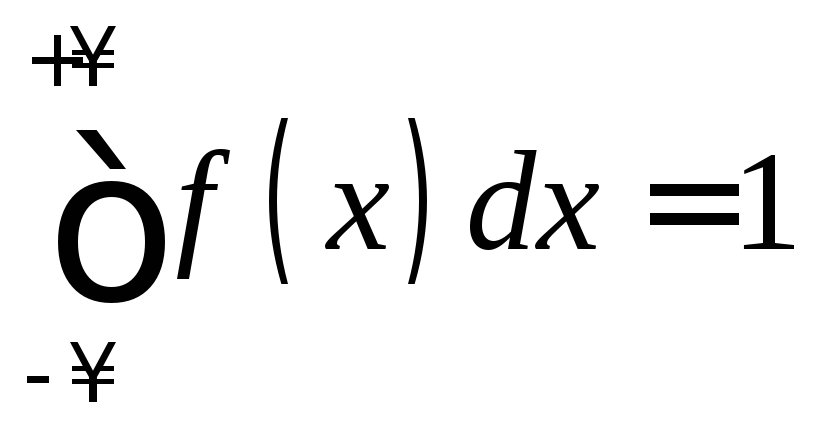Доказательство:

§4. Числовые характеристики дискретной случайной величины

Закон распределения вероятностей содержит полную информацию о случайной величине. В ряде случаев можно сократить эту информацию и воспользоваться числовыми характеристиками.

• Математическим ожиданиемдискретной случайной величины называется сумма всех возможных произведений значений случайной величины на их вероятности:.

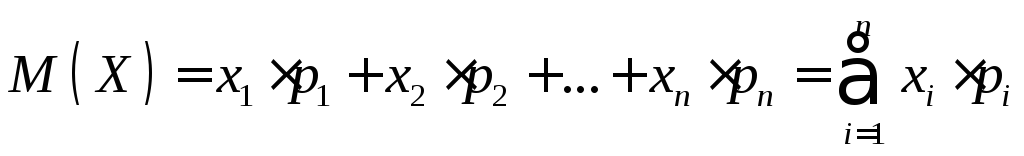Математическое ожидание характеризует центр распределения и оно приближенно равно среднему арифметическому всех возможных значений случайной величины.

Свойства математического ожидания:

1. Если все значения случайной величины Х принадлежат промежутку [a;b], то математическое ожидание не может быть меньшеaи большеb.

2. Математическое ожидание постоянной равно самой постоянной: .

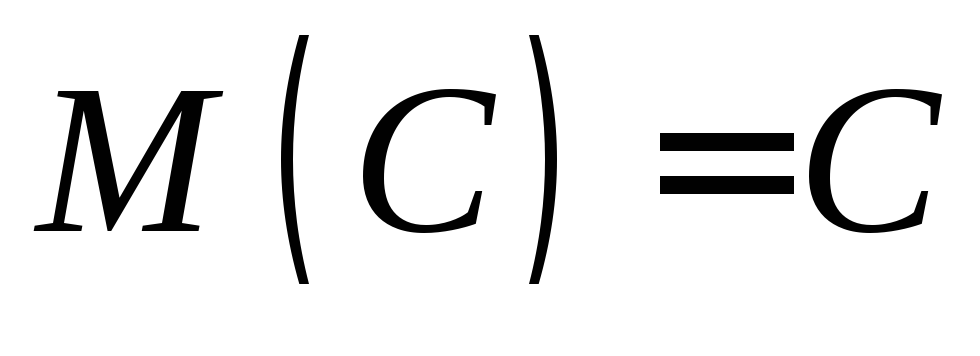Доказательство:

3. Постоянный множитель может быть вынесен за знак математического ожидания: .

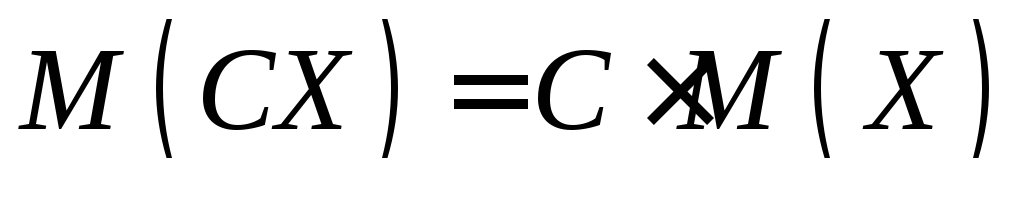Доказательство:

4. Математическое ожидание суммы или разности двух случайных величин равно сумме или разности их математических ожиданий: .

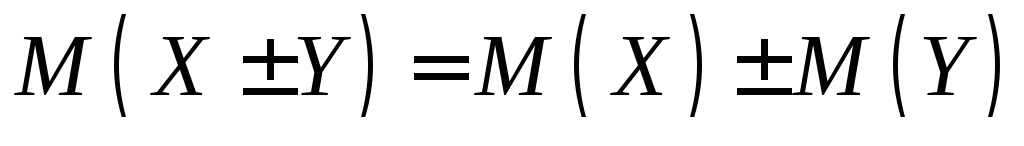5. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: .

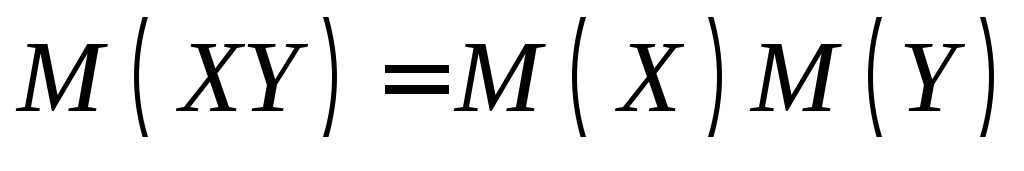Замечание: Две случайные величины называются независимыми, если вероятности, с которыми каждая из них принимает свои значения, не зависят от того, какое значение приняла другая величина.

6. Математическое ожидание отклонения равно нулю: .

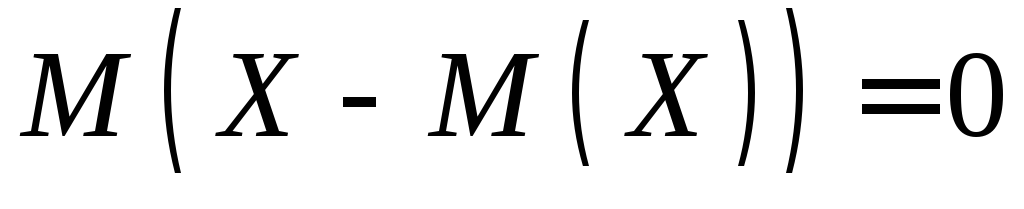Замечание:Отклонениемслучайной величины Х от ее математического ожидание называется разность между случайной величиной Х и ее математическим ожиданием.

Математическим ожиданиемнепрерывной случайной величиныназывается несобственный интеграл. Для него характерны те же свойства, что и для математического ожидания дискретной случайной величины.

• Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: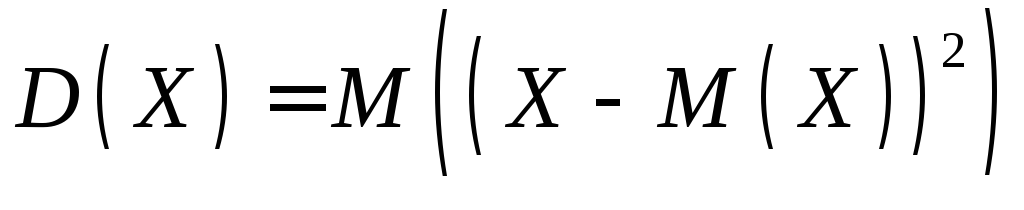. Дисперсия характеризует разброс значений случайной величины относительно математического ожидания. Вычисление дисперсии лучше производить по формуле:

,

где (для дискретной случайной величины) и(для непрерывной случайной величины).

Доказательство:

Свойства дисперсии:

1. Дисперсия всегда неотрицательна: .

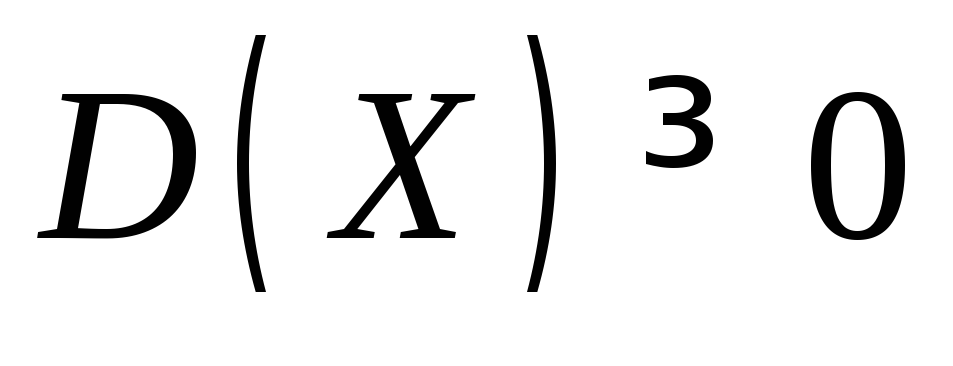2. Дисперсия постоянной равна нулю: .

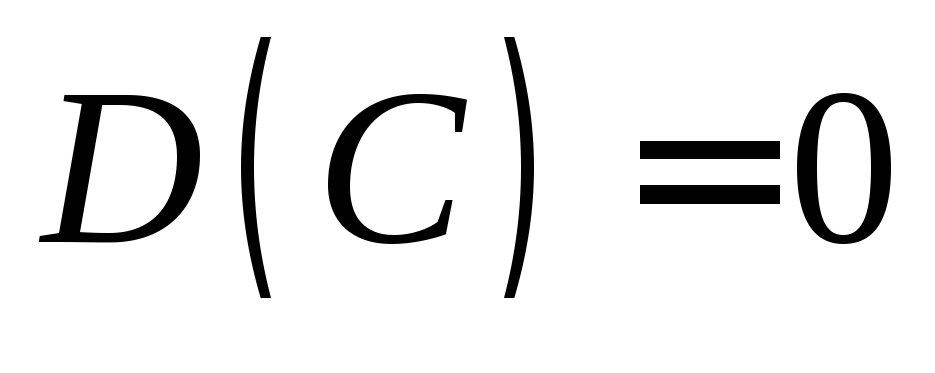3. Постоянный множитель может быть вынесен за знак дисперсии, возведенный в квадрат: .

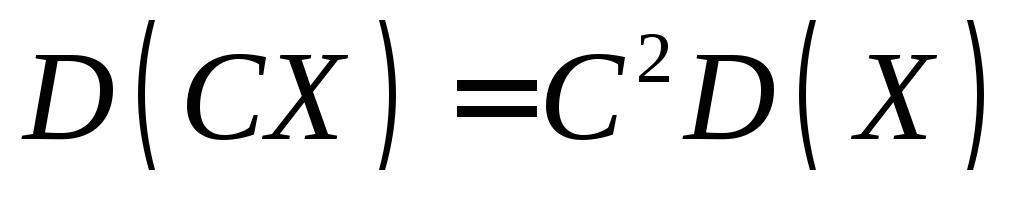Доказательство:

4. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: .

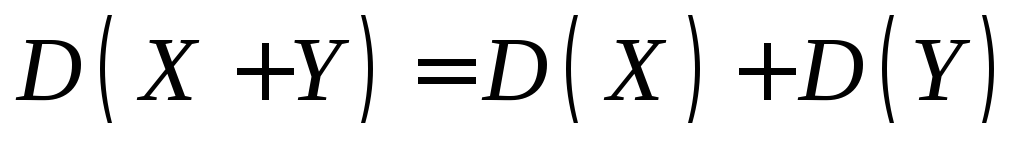5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: .

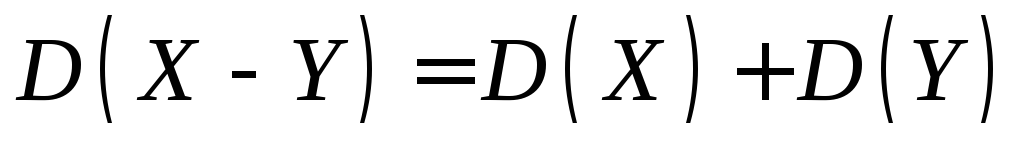6. Дисперсия суммы случайной величины Х и постоянной величины равна дисперсии случайной величины Х: .

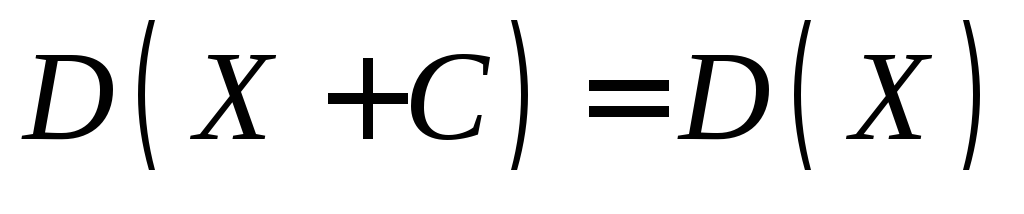• Недостатком дисперсии является то, что ее размерность равна размерности квадрата случайной величины, поэтому в ряде случаев для описания разброса используют среднеквадратическое отклонение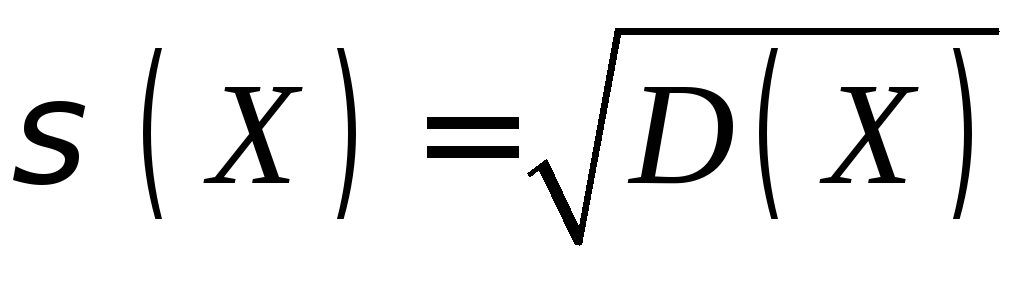, которое имеет ту же размерность, что и сама случайная величина.

Рассмотренные числовые характеристики являются основными. Наряду с ними рассматриваются и другие числовые характеристики:

• Модойдискретной случайной величины Х называют то значениех_i, которое достигается с наибольшей вероятностью.

Модой непрерывной случайной величины называется точка максимума плотности распределения вероятностей.

Мода обозначается .

Распределение может не иметь моды вообще, иметь одну моду (унимодальное), две (бимодальное) или несколько мод (полимодальное).

• Медианойслучайной величины называют такое ее значение, для которого значение функции распределения вероятностей равно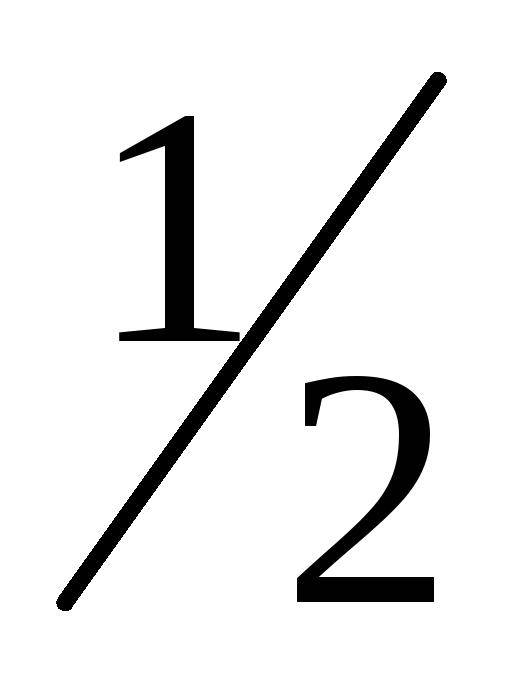. Обозначается..

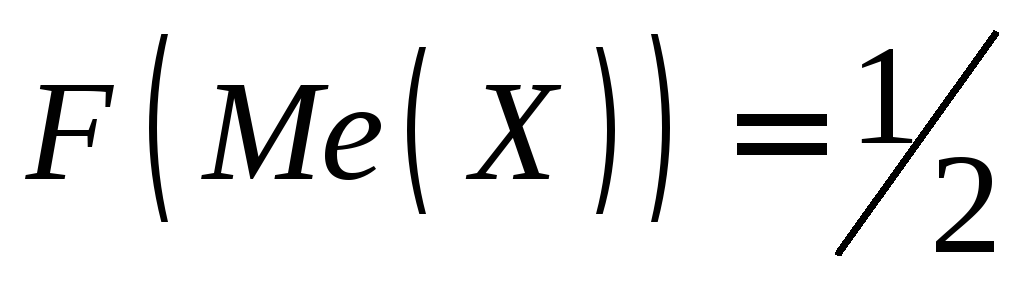• Начальным моментом k-го порядкаслучайной величиныXназывается математическое ожиданиеk-й степени этой величины:.

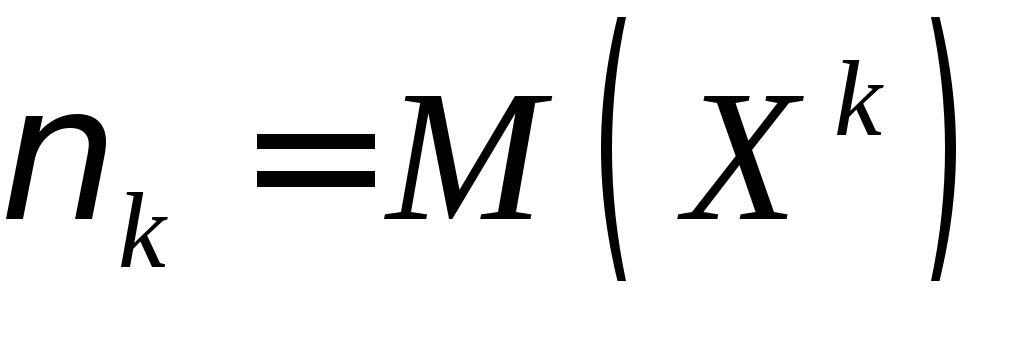Например:

Начальные моменты вычисляются по следующим формулам:

- для дискретной случайной величины ;

- для непрерывной случайной величины .

• Центральным моментом k-го порядкаслучайной величиныXназывается математическое ожиданиеk-й степени отклонения этой величины от ее математического ожидания:.

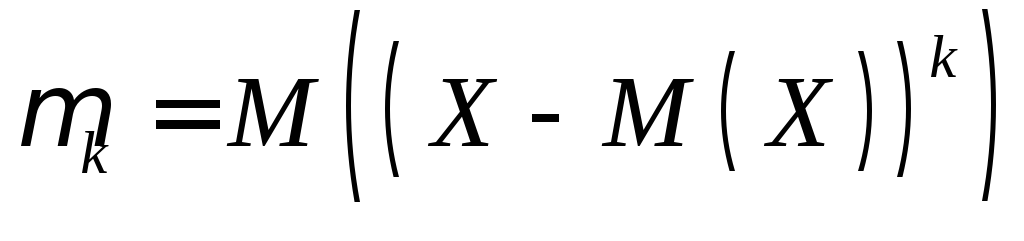Например:

Центральные моменты лучше вычислять с помощью начальных моментов по следующим формулам:

Центральный момент третьего порядка характеризует симметричность распределения.

• Коэффициентом асимметрииназывают число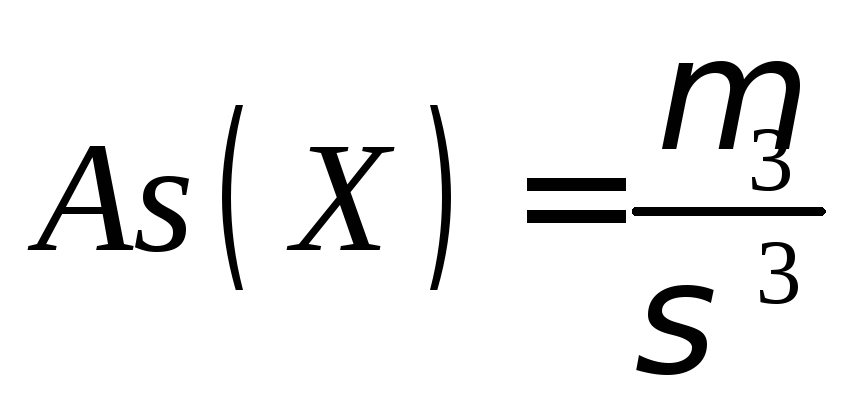. У симметричных распределений этот коэффициент равен нулю. Если «длинная» часть кривой расположена справа от моды, коэффициент асимметрии больше нуля, если слева – меньше нуля.

• Коэффициентом эксцесса случайной величины Х называют число, определяемое формулой: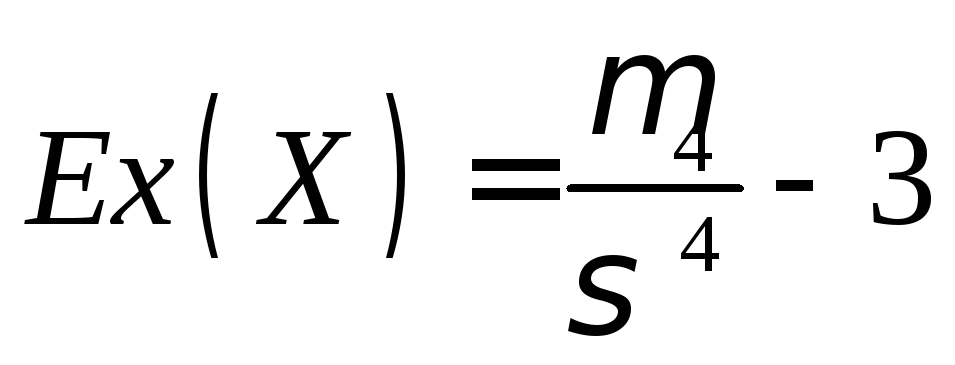. Эксцесс служит для оценки «крутости» распределения, то есть большего или меньшего подъема кривой по сравнению с нормальным распределением с тем же математическим ожиданием и среднеквадратическим отклонением. У нормального распределения коэффициент эксцесса равен нулю. Если кривая более высокая и острая, то коэффициент эксцесса больше нуля. Если более низкая и пологая – меньше нуля.