5 курс / ОЗИЗО Общественное здоровье и здравоохранение / Статистический_анализ_данных_в_медицинских_исследованиях_в_2_ч_Красько

Рис.11–3. Возможное расположение доверительных интервалов для исследований полноценности

Для исследований эквивалентности предельное значение 0 ограничивает

расположение интервала и слева и справа. Расположение доверительных интервалов может быть следующим (Рис. 11–4):

Эквивалентно

Неэквивалентно

Эквивалентно

Неэквивалентно

Рис.11–4. Возможное расположение доверительных интервалов для исследований эквивалентности

Все аналогичные представления могут быть получены не для разности, а для отношения двух пропорций. В этом случае роль эквивалента нулевой разности играет 1 – как равенства отношений этих пропорций. Когда оценивают разность

101

между пропорциям – то говорят, что одна превышает другую (меньше другой) на х%. Когда оценивают отношений пропорций, говорят, что одна превышает другую (меньше другой) в х раз.

11.1.5. Тесты таблиц 2 2

Если вам не нужен подробный анализ, то достаточно уже упомянутых выше тестов.

Точный тест Фишера

Точный тест Фишера (Fisher’s exact test) может применяется для проверки нулевой гипотезы о том, отобраны ли две исследуемые бинарные выборки из двух популяций с одинаковой частотой встречаемости изучаемого эффекта, т.е. есть связь между наличием фактора и исходом.

Тест χ 2 Пирсона (Pearson's Chi-Square Test)

Тест χ 2 Пирсона (Pearson's Chi-Square Test) – универсальный тест для таблиц

сопряженности, применятся для анализа частот в таблицах любых размерностей, в том числе таблиц 2 2, если ожидаемые частоты в ячейках таблицы больше 5.

Двухвыборочный тест пропорций

Двухвыборочный тест пропорций может использоваться для сравнения двух пропорций, и основан на независимой случайной выборке размера m из первой популяции и независимой случайной выборке размера n из второй популяции.

Основное предположение – предположение случайного осуществления выборки от этих двух популяций.

выдвигаем гипотезу H0 :π1 π2 0 , альтернативная гипотеза H0 :π1 π2 0. Пусть k1 количество наблюдений выборки 1 с интересующим эффектом, k2 –

количество наблюдений выборки 2 с интересующим эффектом. Рассчитаем оценки пропорций пропорции πˆ1 k1 m и πˆ2 k2 n , πˆ k1 k2 m n .

Рассчитываем значения mπˆ1 , m 1 πˆ1 ,nπˆ2 и n 1 πˆ2 . Если все эти значения

больше или равны 5, переходим к следующим шагам. В ином случае необходим точный тест Фишера.

Рассчитываем z πˆ1 πˆ2 πˆ 1 πˆ 1m 1n .

то нулевая гипотеза может быть отклонена.

Заметим, что интересующим эффектом может быть не только состояние (“данет”). Например, можно сравнить количественную переменную, закодировав состояние ниже нормы как 0, выше нормы – как 1 и т.п.

Этот тест основан на том, что биноминальное распределение может быть аппроксимировано нормальным распределением, когда события (состояния) не являются редкими. Фактически расчет z – это нормализация разности пропорций, и тест сравнивает нормализованное значение со стандартным нормальным распределением.

102

Пример

Клинические исследования двух препаратов. Условные данные приведены в Табл. 11–7.

Таблица 11–7. Данные примера

Результаты расчета:

πˆ1 0,33; πˆ2 0,83;

δ πˆ2 –πˆ1 0,5;

Нулевая гипотеза: вероятности исходов равны H0 :π1 π2 . Альтернативная HA :π1 π2 . Точный двусторонний критерий Фишера дает уровень значимости 0,015. Нулевая гипотеза о равенстве вероятностей отклоняется.

Расчет доверительного интервала для разности двух пропорций:

δU 0,5 0,34 0,84 .

Как видно, точечная оценка разности больше нуля, доверительный интервал не включает 0, поэтому можно утверждать, что пропорции различаются на уровне значимости α 0,05 ; 33% пациентов в группе А ответили на лечение в сравнении с

83% пациентов в группе В (Точный критерий Фишера p=0,015). Размер эффекта составил 50%, 95% доверительный интервал 16%–84%.

103

Вывод: Препарат В повышает вероятность благоприятного исхода у исследуемой группы на 50% (95% доверительный интервал 16%–84%) в сравнении

спрепаратом А по результатам лечения в группах пациентов на уровне значимости

α0,05 .

Теперь рассмотрим отношение шансов. OR 10 , 95% доверительный интервал (1,44; 69,26). Доверительный интервал не включает в себя значение единица (1), это свидетельствует о том, что препарат В превосходит препарат А по эффективности исходов. Размер эффекта препрарата В в данном случае в 10 (1,44; 69,26) раз выше в сравнении с препраратом А.

Вывод: 33% пациентов в группе А ответили на лечение в сравнении с 83% пациентов в группе В. Шансы ответа на лечение в группе В в 10 раз (95% доверительный интервал (1,44; 69,26)) выше по отношению к шансам группы А.

В Приложении R-7 содержатся R-скрипты для расчетов данного примера: разности пропорций, отношения шансов, и их доверительных интервалов.

Основные аспекты

Количественную переменную можно представлять как биноминальную переменную, однако это снижает информативность вашего исследования.

В зависимости от цели исследования нужно понимать, что именно исследуется: неблагоприятный исход; эффект лечения; фактор риска или фактор, снижающий риск, поскольку тестом (Фишера, Пирсона) можно определить только наличие взаимосвязи, а статистическая оценка размера эффекта для бинарных исходов в двух группах более детально изучается с помощью разности в пропорциях, отношений шансов, доверительных интервалов.

104

12. Бивариантый анализ: биноминальная и количественная переменные

Биноминальная переменная разбивает количественную переменную на две группы. По взаиморасположению графиков частот или гистограмм можно визуально отобразить расположение двух групп. На рис. 12–1 представлены различные варианты расположения распределений количественной переменной в двух группах.

а) Интервалы не пересекаются, группы разделены по расположению.

б) Группы разделены частично по расположению.

105

Группа 2:Доверительный интервал для среднего

Группа 1: Доверительный интервал для среднего

в) Группы имеют различную дисперсию , при одинаковом среднем.

Доверительный интервал для среднего

г) Нет разделения.

Рис.12–1. Варианты расположения двух выборочных распределений

Как видно, ситуации бывают разные, необходимо проверять как местоположение, так и рассеяние распределений. Чем больше у вас будет визуального материала, тем легче будет понимание ваших данных.

Достаточно наглядным будет отображение двух групп с помощью графика “ящик с усами”, Q-Q графики и пр.

Общий подход к анализу биноминальной и количественной переменной – это анализ двух групп, представленных количественной переменной.

106

Существует множество тестов, которые проверяют взаиморасположение двух выборочных распределений.

Нулевая гипотеза утверждает, что два распределения одинаковы. Выбор критерия зависит от типа альтернативной гипотезы. Тестируется или положение распределения (среднее, медиана), или рассеяние (масштаб). В таблице ниже приведена классификация тестов по тестируемым параметрам.

Параметрические тесты основываются на знании закона распределения, оперируя с параметрами такого распределения. Предположение о законе распределения должно быть проверено перед применением таких тестов (проверка предположения, лежащего в основе теста о том, что данные подчиняются закону нормального распределения, для каждой из групп). В непараметрических тестах знания закона распределения не требуется, но такие тесты являются менее мощными. Самый частый прием при вычислении непараметрических статистик – это присвоение рангов числовому ряду.

В линейных ранговых тестах исходные значения измерений заменяются на некоторые ранги, которые имеют тот же порядок (в смысле возрастания и убывания), что и исходные данные. Ранговые тесты различаются по способу построения такой порядковой шкалы.

Основные тесты двух групп приведены в Табл. 12–1.

Таблица 12–1. Тесты количественной переменной для двух групп

Критерий Вилкоксона–Манна–Уитни (Wilcoxon-Mann-Whitney Test)

Критерий Вилкоксона–Манна–Уитни (В некоторых источниках его называют критерием Манна–Уитни) используется для определения “сдвига”, что означает, что два распределения имеют одинаковую форму, но одно из них сдвинуто относительно другого на определенную величину. Критерий непараметрический.

107

Критерий нормальных рангов (Van der Waerden test , Normal Scores Test)

Ранговый критерий. Альтернатива тесту Вилкоксона–Манна–Уитни, также используется для определения “сдвига”. Критерий непараметрический.

Тест рангов Сэвиджа (Savage Scores Test)

Используется, если сравниваются две выборки, взятые из экспоненциального распределения. Критерий непараметрический.

Критерий Сиджела-Тьюки (Siegel-Tukey Test1)

Критерий используется для проверки гипотезы, что две выборки взяты из одного распределения против гипотезы о том, что выборки имеют одинаковый параметр положения (среднее или медиану), но разные дисперсии. Критерий непараметрический

Критерий Ансари-Бредли (Ansari-Bradley Test)

Критерий Ансари-Бредли – альтернатива тесту Сиджела-Тьюки. Критерий непараметрический.

Критерий Клотца (Klotz test)

Критерий Клотца – альтернатива тесту Сиджела-Тьюки. Критерий непараметрический.

Китерий Муда (Mood test)

Китерий Муда – альтернатива тесту Сиджела-Тьюки. Критерий непараметрический.

Критерий Коновера (Conover test)

Критрий Коновера – альтернатива тесту Сиджела-Тьюки. Критерий непараметрический. Тест более общий, не нуждается в предположении, что параметр положения у двух популяций известен или одинаков.

F-критерий Фишера (Fisher F-test)

F-тест Фишера (критерий Фишера-Снедекора) применяют для сравнения дисперсий двух нормальных выборочных совокупностей. Критерий часто называют дисперсионным отношением или просто статистикой Фишера. Широко используется в анализе вариаций (Analysis of Variance, ANOVA) для сравнения трех и более выборок.

Тест Стьюдента для независимых выборок

Критерий Стьюдента для независимых выборок (two-group unpaired t-test) предназначен для проверки нулевой гипотезы о равенстве средних значений двух нормальных выборочных совокупностей в случае равных неизвестных дисперсий. Предварительно необходимо проверить, что данные подчиняются закону нормального распределения (для каждой из групп), а также сравнить дисперсии групп F-тестом, поскольку тест Стьюдента используется для данных, взятых из нормального распределения при равенстве дисперсий двух выборок. В случае неравных дисперсий используется тест Уэлча.

1 Часто можно найти название теста – критерий Зигеля-Тьюки. Sidney Siegel был американским психологом. Правильное прочтение оставляю за читателями.

108

Тест Уэлча (Walсh test, Satterthwaite’s test)

Тест Уэлча (критиерий Велча, Крамера-Уэлча, Саттерзвайта) предназначен для проверки нулевой гипотезы о равенстве средних значений двух нормальных выборочных совокупностей в случае неравных неизвестных дисперсий.

12.1. Анализ двух групп: Характеристическая кривая (receiver operating characteristic(ROC) curve)

После того, как выяснено, что две группы значимо различаются в среднем, можно определить, где находится "граница" между двумя группами. Если значимой разницы в местоположении двух групп нет, то такую точку определить невозможно, а точнее говоря, она не будет информативной. Поэтому ROC–анализ имеет смысл использовать после того, как тесты двух групп (t-тест или его аналоги, тест МаннаУитни или его аналоги) показали значимость различия в местоположении. Если тесты положения не являются значимыми, то построение характеристической кривой также даст незначимые результаты.

Характеристическая кривая строится по мерам чувствительности и специфичности.

Построение ROC-кривой рассмотрим на примере.

Пример

Данные приведены в табл.12–2.

Таблица 12–2. Данные примера

Шаг 1. Количественная переменная упорядочивается по возрастанию. Предположим, что заболевание связано с низким значением показателя.

Шаг 2. Для каждого значения количественной переменной рассчитывается таблица 2 х 2, как описано в Табл. 12–3. На основе таблиц для каждого значения показателя xi рассчитываются значения Sni Ai n и Spi Di 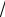m .

Проще говоря, каждое значение количественной переменной по очереди принимается за порог (границу), формируется таблица 2 2 и по ней рассчитываются характеристики чувствительности и специфичности. В Табл. 12–4 приведены расчеты.

109

110