
Функциональный(конспекты и вопросы в конце)
.pdf
Глава 4
Интеграл Лебега
4.1. Предварительные замечания об интеграле Лебега
Для конечного множества X = {x1, . . . , xn} с мерой µ, по которой каждое подмножество измеримо, интеграл Лебега определяют от любой функции вида
формулой |
|
f : X → R |
||
∫ |
|
∑ |
|
|
|
|
|
||
|
f(x)dµ := |
n |
f(xi)µ(xi), |
|
Xi=1
причем сумму в этой формуле следует вычислять, используя арифметику расширенной чис-
ловой прямой R.
Пример 4.1.1. Пусть
X = {x1, x2, x3}, µ(x1) = |
1 |
, µ(x2) = 1, µ(x3) = |
1 |
, |
|||||||||||
|
2 |
3 |
|||||||||||||
f : X → R, f(x1) = −1, f(x2) = 3, f(x3) = |
1 |
. |
|
|
|||||||||||
|
|
|
|||||||||||||
8 |
|
|
|||||||||||||
Тогда |
|
|
1 |
1 |
61 |
|
|
|
|
||||||
1 |
|
|
|
|
|
||||||||||
X∫ f(x)dµ = (−1) · |
|
|
+ 3 · 1 + |
|
· |
|
= |
|
|
|
|
|
|
||
2 |
8 |
3 |
24 |
|
|
|
|
||||||||
Заметим, что для некоторых конечных множеств с мерой и функций на них интеграл Лебега может быть неопределен, например, как в следующем примере.
Пример 4.1.2. Пусть
X = {x1, x2}, µ(x1) = 1, µ(x2) = ∞, f : X → R, f(x1) = ∞, f(x2) = −1.
Тогда интеграл |
∫ |
f(x)dµ = (∞) · 1 + (−1) · ∞ = ∞ − ∞
X
неопределен.
Âобщем случае, интеграл Лебега определяется на произвольном пространстве X с мерой
µ(например, на произвольном вероятностном пространстве). Определяется интеграл Лебега по следующему плану.
(1)Рассматриваются функции вида
(4.1.1) |
f : X → R |
и среди них выделяются измеримые функции.
(2)Среди измеримых функций выделяются интегрируемые по Лебегу функции.
(3)Для интегрируемых по Лебегу функций (и только для них) определяется равный конечному числу интеграл Лебега.
51

4.2. ИЗМЕРИМЫЕ ФУНКЦИИ НА ПРОСТРАНСТВЕ С МЕРОЙ |
52 |
Множество интегрируемых по Лебегу функций обозначается через L1(X, µ), а интеграл Ле-
áåãà îò f L1(X, µ) обозначается через
∫
fdµ.
X
На интуитивном уровне, интеграл Лебега есть сумма значений функции f по точкам пространства X, причем каждая точка учитывается с мерой.
Всюду в этой главе, говоря о функциях на пространстве с мерой, мы будем подразумевать функции вида (4.1.1).
4.2. Измеримые функции на пространстве с мерой
Фиксируем пространство X с мерой µ.
Определение 4.2.1. Функцию f на пространстве X называют измеримой по мере µ, если для всякого отрезка [a, b] R (случаи a = −∞ è b = ∞ допускаются) его прообраз f−1([a, b]) измерим. Измеримые по мере функции называют также просто измеримыми.
Пример 4.2.2. Всякая непрерывная на Rn функция измерима по Лебегу.
Пример 4.2.3. Xарактеристическая функция
{
1A(x) :=
0, åñëè x / A,
1, åñëè x A
подмножества A X измерима тогда и только тогда, когда подмножество A измеримо.
Теорема 4.2.4. Åñëè f1, . . . , fm ограниченные измеримые функции на X è g(z1, . . . , zm)непрерывная функция от переменных z1, . . . , zm, то функция g(f1, . . . , fm) измерима.
Из этой теоремы следует, что модуль измеримой функции, а также сумма и произведение измеримых функций измеримы. Следующая теорема утверждает, что предел (в любом смысле) измеримых функций измерим.
Теорема 4.2.5. Пусть (X, µ) пространство с мерой, {fn} последовательность измеримых функций на X è f функция на X. Утверждается, что в каждом из следующих случаев
(1) f = sup fn; |
(2) f = inf fn; |
|
(3) f = lim sup fn; |
(4) f = lim inf fn; |
|
(5) fn −→ f; |
(6) fn f; |
ï.â. |
(7) fn −→ f |
||
функция f измерима.
Теорема 4.2.6 (теорема Лузина). Функция вида f : [a, b] → R измерима по Лебегу тогда
и только тогда, когда для любого ε > 0 существует непрерывная функция fε : [a, b] → R такая, что
λ({x [a, b] | f(x) ≠ fε(x)}) < ε.
Грубо говоря, теорема Лузина утверждает, что всякая измеримая и принимающая конеч- ные значения функция на отрезке "приблизительно" является непрерывной функцией.
Для измеримых функций на пространстве с мерой определим еще один тип сходимости сходимость по мере.
Определение 4.2.7. Говорят, что последовательность {fn} измеримых функций сходится по мере к измеримой функции f и пишут
µ
fn −→ f,
4.2. ИЗМЕРИМЫЕ ФУНКЦИИ НА ПРОСТРАНСТВЕ С МЕРОЙ |
53 |
если для любого ε > 0 имеем
nlim µ ({x X | |fn(x) − f(x)| > ε}) = 0. |
|||
→∞ |
|
|
|
Пример 4.2.8. На прямой R с мерой Лебега рассмотрим последовательность функций |
|||
fn : R → R, |
1, |
ïðè x |
[n, n + 1], |
fn(x) = {0, |
ïðè x |
[n, n + 1]. |
|
|
|
|
̸ |
Нетрудно заметить, что последовательность {fn} сходится поточечно к нулевой функции,
но не сходится по мере, не сходится почти всюду и не сходится равномерно к какой-либо функции.
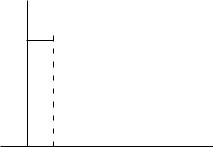
Пример 4.2.9. На отрезке [0, 1] с мерой Лебега рассмотрим последовательность функций
fn : [0, 1] |
→ |
R, |
fn(x) = |
1, |
ïðè x |
[0, n1 ], |
|
|
|
|
{0, |
ïðè x |
[n1 |
, 1], |
|
|
|
|
|
|
|
̸ |
|
6
1
fn(x)
0 |
1 |
1 |
-x |
n |
Нетрудно заметить, что последовательность {fn} сходится поточечно, по мере и почти всюду к функции
|
0, |
åñëè 0 < x |
1, |
f : [0, 1] |
→ R, f(x) = {1, |
åñëè x = 1,6 |
|
но не сходится равномерно к какой-либо функции.
Пример 4.2.10. Рассмотрим отрезок [0, 1] с мерой Лебега. Для n N è 1 6 m 6 n определим функцию
fnm : [0, 1] |
→ |
R, |
fnm(x) = |
1, |
ïðè x |
[mn−1 |
, mn ], |
|
|
|
|
{0, |
ïðè x |
[mn−1 |
, mn ] |
||
|
|
|
|
|
|
̸ |
|
|
и рассмотрим последовательность функций
f11, f21, f22, f31, f32, f33, . . . , fn1, fn2, . . . , fnn, . . .
Нетрудно заметить, что эта последовательность сходится к нулевой функции по мере, но не сходится почти всюду, не сходится поточечно и не сходится равномерно к какой-либо функции.
Теорема 4.2.11. Рассмотрим последовательность {fn} измеримых функций на X.
(1)Если последовательность {fn} равномерно сходится к функции f, то она сходится к этой функции почти всюду и по мере.
(2)Åñëè µ(X) < ∞ и последовательность {fn} сходится почти всюду к функции f, то она сходится к этой функции по мере.
4.3. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА ЛЕБЕГА |
54 |
Доказательство. (1) очевидно.
(2). Фиксируем ε > 0 и положим
|
An(ε) = {x X | |f(x) − fn(x)| > ε}, |
|
|
|||||
|
Bk(ε) = An(ε). |
|||||||
|
|
|
|
|
|
|
|
n>k |
Имеем включения |
|
|
|
|
|
|
|
|
|
B1(ε) B2(ε) B3(ε) . . . . |
|||||||
Из условия теоремы и утверждения (1) задачи 3.6.13 получаем |
||||||||
|
|
|
∩ |
|
)) |
|
|
|
(4.2.1) |
0 = |
µ |
B |
ε |
lim µ(B |
ε . |
||
|
( |
n>1 |
n( |
= n→∞ |
|
n( )) |
||
|
|
|
|
|
|
|
|
|
Отсюда и из включения An(ε) Bn(ε) следует |
|
|
|
|||||
|
|
|
lim µ(An(ε)) = 0, |
|
|
|||
|
µ |
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что и означает, что fn −→ f. |
|
|
|
|
|
|
||
Примеры 4.2.9 и 4.2.10 показывают, что из сходимости по мере не следует сходимость почти всюду, а из сходимости почти всюду не следует равномерная сходимость. С другой стороны, как показывают следующие ниже теорема 4.2.12 и теорема Егорова, из сходимости последовательности измеримых функций по мере следует некоторое утверждение о сходимости почти всюду, а из сходимости последовательности измеримых функций почти всюду следует некоторое утверждение о равномерной сходимости.
Теорема 4.2.12. Пусть последовательность {fn} измеримых функций на пространстве с мерой X сходится по мере к функции f. Тогда существует подпоследовательность этой последовательности, сходящаяся к f почти всюду.
Теорема 4.2.13 (Теорема Егорова). Пусть (X, µ) пространство с мерой, µ(X) < ∞ и последовательность {fn} измеримых функций на X стремится к функции f почти всюду. Тогда для любого ε > 0 существует подмножество Eε X такое, что
µ(Eε) < ε è fn|X\E" f|X\E"
Грубо говоря, теорема Егорова утверждает, что всякая поточечно сходящаяся последовательность функций на пространстве с конечной мерой "приблизительно" является равномерно сходящейся.
4.3. Определение интеграла Лебега
Фиксируем пространство X с мерой µ.
Определение 4.3.1. Функцию f на пространстве X, называют простой, если она может
быть представлена в виде |
|
∑ |
|
|
|
(4.3.1) |
f = |
fi1Ai , |
16i6n
ãäå A1, . . . , An X измеримые подмножества, f1, . . . , fn R.
Например, на R с мерой Лебега λ функция Дирихле является простой, на любом конечном отрезке [a, b] с мерой Лебега λ функция
f(x) = [x] (целая часть числа x)
является простой.
4.3. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА ЛЕБЕГА |
55 |
В определении 4.3.1 разложение (4.3.1) всегда не единственно. Например,
0 = 1X − 1X .
Ясно, что простые функции измеримы.
Лемма 4.3.2. Пусть (X, µ) пространство с мерой. Тогда для всякой простой функции
существует единственное разложение вида |
|
∑ |
|
f = |
fi1Ai , |
16i6n |
|
ãäå |
|
|
|
X = |
Ai, |
|
16i6n |
A1, . . . , An X измеримые подмножества и f1, . . . , fn попарно различные действитель- ные числа.
Разложение, существование которого утверждается в этой лемме, называют канониче- ским.
Определение 4.3.3. Измеримую функцию f на пространстве X называют интегрируемой по Лебегу в следующих индуктивно определяемых случаях.
(Leb1) Функция f простая и |
∑ fi1Ai |
f = |
16i6n
ее каноническое разложение; в этом случае
∫∑
fdµ := |
fiµ(Ai). |
X16i6n
(Leb2) Функция f неотрицательна и |
|
|
|
|
|
|
|
||
g простая, |
|
|
|
|
|
||||
|
6 6 |
|
X |
|
|
< ; |
|
||
|
sup |
|
∫ |
gdµ |
|
||||
0 g f |
|
|
|
∞ |
|
|
|||
в этом случае |
|
|
|
|
|
|
|
||
∫ |
|
g простая, |
|
|
|
||||
|
|
|
|
|
∫ |
|
|
|
|
fdµ := |
sup |
|
gdµ |
|
. |
||||
|
|
|
06g6f |
|
|
||||
X |
|
|
X |
|
|
|
|||
(Leb3) В разложении f = f+ − f− (см. задачу 4.6.2) неотрицательные функции f+ è f−
интегрируемы по Лебегу; в этом случае
∫ ∫ ∫
|
fdµ := |
f+dµ − f−dµ. |
X |
X |
X |
Мы опускаем довольно длинное техническое доказательство того, что это определение корректно. Множество интегрируемых по Лебегу функций на пространстве с мерой (X, µ)
обозначают через L1(X, µ).
Пример 4.3.4. Постоянная функция f(x) ≡ c интегрируема по Лебегу тогда и только
тогда, когда c = 0 èëè µ(X) < +∞ и в этих случаях
∫
cdµ = cµ(X).
X

4.4. СВОЙСТВА ИНТЕГРАЛА ЛЕБЕГА |
56 |
Пример 4.3.5. Пусть f(t) функция Дирихле. Тогда
∫
fdλ = 0
[0,1]
(заметим, что интеграл Римана ∫01 f(t)dt не существует).
Естественным образом определяют интеграл Лебега от комплекснозначных функций. А именно, на пространстве X с мерой µ рассматривают комплекснозначные функции вида
(4.3.2) |
f(x) = f1 |
√ |
|
|
|
||||
|
(x) + −1f2(x), |
|||
ãäå
f1, f2 : X → R.
Функцию вида (4.3.2) называют
•измеримой, если измеримыми являются f1 è f2;
•интегрируемой по Лебегу, если интегрируемыми являются функции f1 è f2; â ýòîì случае интеграл Лебега от f полагают равным
∫∫ √ ∫
|
fdµ := |
f1dµ + −1 f2dµ. |
X |
X |
X |
4.4. Свойства интеграла Лебега
Интеграл Лебега и интеграл Римана.
В анализе имеется развитая техника для практических вычислений интегралов Римана. При вычислениях интегралов Лебега по мере Лебега на Rn их, как правило, сводят к вычис-
лениям соответствующих интегралов Римана, используя следующую теорему.
Теорема 4.4.1. Пусть f(t1, . . . , tn) неотрицательная, непрерывная в области D Rn функция. Утверждается, что f(t1, . . . , tn) интегрируема по Лебегу на D по мере Лебега тогда и только тогда, когда f(t1, . . . , tn) интегрируема по Риману на D (возможно несоб-
ственно), причем в этом случае
∫ ∫
fdλ = f(t1, . . . , tn)dt1 . . . dtn.
D D
Например, |
∫ |
|
∫ |
|
∫ |
|
∫ |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
2 |
|
|
1 |
|
|||||
|
|
tdλ = |
|
|
tdλ + |
tdλ = |
0 |
tdt = |
t |
0 |
= |
, |
||
|
|
|
|
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[0,1] |
0 |
1 |
} |
(0,1) |
|
|
|
|
|
|
|
|
|
|
|
{ |
} { |
|
|
|
|
|
|
|
|
|
|
|
∫ |
1 |
1 |
1 |
|
= |
1 |
1 |
|||
√t |
∫0 |
√t |
|
ε→0+ ∫ε |
√t |
|||||
|
|
|
dλ = |
|
|
dt |
|
lim |
|
|
(0,1)
Теорема Радона-Никодима.
Пусть (X, µ) пространство с мерой.
√ 1
dt = lim 2 t = 2.
ε→0+ ε
Определение 4.4.2. Пусть f измеримая функция на X è A измеримое подмножество в X. Если ограничение f|A функции f íà A интегрируемо по Лебегу на A ïî ìåðå µ|A, òî
говорят, что функция f интегрируема по Лебегу на A относительно меры µ и интеграл
∫ ∫
f|A d(µ|A) обозначают через fdµ.
A A
Лемма 4.4.3. Пусть f интегрируемая по Лебегу на X функция и A измеримое подмножество в X. Тогда функция f интегрируема по Лебегу на A ïî ìåðå µ.

4.4. СВОЙСТВА ИНТЕГРАЛА ЛЕБЕГА |
57 |
Лемма 4.4.4. Пусть f интегрируемая по Лебегу на X функция. Тогда если
A = Ai,
i I
ãäå I не более чем счетно и каждое подмножество Ai измеримо, то
∫ ∑ ∫
fdµ = fdµ,
Ai I Ai
причем ряд в правой части равенства сходится абсолютно.
Следствие 4.4.5 (Абсолютная непрерывность интеграла Лебега) . Пусть f интегри-
руемая по Лебегу функция на X. Тогда для любого ε > 0 существет δ > 0 такое, что |
|
|||||||||||||||
|
A |
|
X измеримо, µ(A) < δ |
= |
|
|
|
fdµ < ε. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A è An, n |
|
N |
Следствие 4.4.6. Пусть f интегрируемая по Лебегу на |
X функция, |
|
||||||||||||||
измеримые подмножества в X. Тогда |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
An ↑ A |
èëè |
|
|
|
|
|
|
|
|
|
|
|
|
|
An |
A |
èëè |
|
|
∫ |
|
−→ |
∫ |
|
|
|
||||
|
|
|
−→ µ |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
èëè |
|
= |
|
An |
fdµ |
|
|
A |
|
|
|
|
|
An ↓ A |
|
|
|
|
|
fdµ |
|
|
|
||||||
(грубо говоря, |
|
|
An −→ A |
|
|
|
|
|
"хорошо ведет cебя" при пре- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
A∫ |
fdµ |
|
|
|
|
|
|
|
дельных переходах по A). |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
утверждается, что интеграл Лебега |
|
|
|
|
|
|
|
||||||||
Следствие 4.4.7. Всякая неотрицательная интегрируемая по Лебегу на X функция f определяет меру µf íà X. А именно, µf -измеримыми подмножествами пространства X являются µ-измеримые подмножества и для всякого такого подмножества A åãî µf -ìåðà
полается равной |
|
|
|
|
µf (A) = |
A∫ |
fdµ. |
|
|
|
|
|
|
|
|||||||||||
Пример 4.4.8. Пусть (X, µ) = ([0, 1], λ), ãäå λ мера Лебега, f(t) = t. Тогда |
|||||||||||||||||||||||||
|
|
|
|
|
µf (A) = A∫ |
tdλ. |
|
|
|
|
|
|
|
||||||||||||
Например, |
([ |
|
|
]) |
∫ |
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|||||
|
µf |
0, |
2 |
= |
1 |
tdλ = |
0 |
|
tdt = |
2 |
0 |
= |
8 |
. |
|||||||||||
Пример 4.4.9. Пусть (X, µ) = (R, λ), ãäå λ мера Лебега, |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
[0, 2 ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
e− |
(t− )2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
f(t) = |
√ |
|
|
|
|
|
|
2 2 |
, |
|
|
|
|
|
|
|
|||||
|
|
|
|
2πσ |
|
|
|
|
|
|
|
|
|||||||||||||
ãäå µ R, σ > 0 параметры. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
µf (A) = A∫ |
1 |
|
|
|
e− |
|
(t− )2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
√ |
|
|
|
2 2 |
|
dλ. |
|
|
|
|
|
||||||||||
|
|
|
|
2πσ |
|
|
|
|
|
||||||||||||||||
Ìåðà µf задает нормальное распределение вероятностей на |
|
R со средним значением µ è |
|||||||||||||||||||||||
среднеквадратичным отклонением σ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4.4. СВОЙСТВА ИНТЕГРАЛА ЛЕБЕГА |
58 |
Теорема 4.4.10 (Теорема Радона-Никодима) . Пусть (X, µ) σ-конечное пространство с мерой и ν абсолютно непрерывная по мере µ ìåðà íà X. Тогда существует неотрицательная интрегрируемая по Лебегу на X ïî ìåðå µ функция f (которую называют производной
Радона-Никодима меры ν ïî ìåðå µ и обозначают через dν |
µ-èçìå- |
|
|
dµ ), такая, что для любого |
|
римого подмножества A имеем |
∫ fdµ. |
|
ν(A) = |
|
|
|
A |
|
Функция f при этом определена однозначно с точностью до прибавления почти всюду равной нулю функции.
Пример 4.4.11. |
|
|
|
|
|
X = {x1, x2, x3}, |
µ(x1) = 1, µ(x2) = 3, µ(x3) = 2, |
||
|
ν(x1) = 4, ν(x2) = 1, ν(x3) = 0. |
|||
Тогда dν = f, ãäå |
|
|
|
|
dµ |
|
|
|
|
|
f(x1) = 4, f(x1) = |
1 |
, f(x1) = 0. |
|
|
|
|||
|
3 |
|||
РассмотримX∫пространство с мерой (X, µ) . |
|
|
||
Интеграл |
fdµ как функция от f. |
|
|
|
Лемма 4.4.12. Пусть f измеримая функция на X, g интегрируемая по Лебегу на X функция, причем 0 6 f 6 g. Тогда функция f интегрируема по Лебегу на X è
∫∫
0 6 fdµ = gdµ.
XX
Лемма 4.4.13 (Линейность интеграла Лебега) . Для любых интегрируемых по Лебегу
функций f1 è f2 их линейная комбинация c1f1 + c2f2 интегрируема по Лебегу, причем
∫ ∫ ∫
(c1f1 + c2f2)dµ = c1 f1dµ + c2 f2dµ.
X X X
В частности, L1(X, µ) является векторным пространством.
Следствие 4.4.14. Измеримая на X функция f интегрируема по Лебегу на X тогда и только тогда, когда ее модуль |f| интегрируем по Лебегу на X причем в этом случае
|
∫ |
|
|
| | |
|
|
|
|
∫ |
|
|
|
|
|
6 |
|
f dµ. |
|
|
fdµ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
XX
Доказательство. Вытекает из леммы 4.4.13 и соотношения
|f| = f + 2f−
Через N(X, µ) мы будем обозначать множество почти всюду равных нулю функций на X. Напомним, что пространства с мерами, которые мы рассматриваем, предполагаются пол-
ными. На таких пространствах, как нетрудно доказать, почти всюду равные нулю функции измеримы.
4.4. СВОЙСТВА ИНТЕГРАЛА ЛЕБЕГА |
59 |
Лемма 4.4.15. Пусть f функция на X. Тогда f N(X, µ) тогда и только тогда, когда
f интегрируема и |
∫ |f|dµ = 0. |
|
|
|
X |
ï.â.
Следствие 4.4.16. Åñëè f è g интегрируемые функции на X è f = g, òî
∫∫
fdµ = gdµ.
|
|
X |
X |
1 |
Следствие 4.4.17. Подмножество N(X, µ) является линейным подпространством в |
||
L |
(X, µ). |
|
|
|
Доказательство. Действительно, для любых f1, f2 N(X, µ) è c1, c2 R имеем |
||
(4.4.1) |
c1f1 + c2f2 6 |c1f1 + c2f2| 6 |c1||f1| + |c2||f2|. |
||
Теперь из интегрируемости f1 è f2 и следствия 4.4.14 получаем интегрируемость |f1| è |f2| откуда, используя лемму 4.4.13, получаем интегрируемость |c1||f1|+|c2||f2| из которой, используя лемму 4.4.12, (4.4.1) и следствие 4.4.14, получаем интегрируемость c1f1 + c2f2. Наконец,
X∫ |c1f1 + c2f2|dµ 6 X∫ (|c1||f1| + |c2||f2|)dµ 6 |c1|X∫ |f1|dµ + |c2|X∫ |f2|dµ = 0. |
|
|
|
"хорошо ведет cебя" при предельных переходах по f. |
X∫ |
В следующих далее теоремах Леви и Лебега утверждается, что интеграл Лебега |
fdµ |
Теорема 4.4.18 (Теорема Леви о монотонной сходимости) . Пусть (X, µ) пространство
с мерой, 0 6 f1 6 f2 6 . . . последовательность интегрируемых по Лебегу функций, причем предел ∫
lim fndµ
n→∞
X
конечен. Тогда функция
интегрируема по Лебегу, причем
f(x) := lim fn(x)
n→∞
∫∫
fdµ = lim fndµ.
n→∞
XX
Теорема 4.4.19 (Теорема Лебега об ограниченной сходимости) . Пусть (X, µ) простран-
ство с мерой и {fn} последовательность интегрируемых по Лебегу функций. Предположим, что
(1) |
| |
fn |
6 g, ãäå g некоторая интегрируемая по Лебегу функция; |
|
|
|ï.â. |
|
(2) |
fn −→ f, ãäå f некоторая функция. |
||
Тогда функция f интегрируема по Лебегу и
∫∫
lim fndµ = fdµ.
n→∞
XX
4.4. СВОЙСТВА ИНТЕГРАЛА ЛЕБЕГА |
60 |
Теорема Фубини.
Для интеграла Лебега имеется теорема Фубини, которая аналогична теореме о повторном интегрировании для интеграла Римана.
Теорема 4.4.20 (Теорема Фубини). Пусть (X, µ), (Y, ν) |
σ-конечные пространства с |
||||||
мерами и f(x, y) µ × ν-измеримая функция на X × Y . |
|
||||||
(1) Åñëè f(x, y) интегрируема по мере µ × ν, òî |
|
|
|||||
(a) существуют повторные интегралы |
∫ |
∫ f(x, y)dµ dν |
|||||
(4.4.2) |
∫ |
∫ f(x, y)dν |
dµ |
è |
|||
|
X |
Y |
|
|
Y |
X |
|
(существование первого повторного интеграла в |
(4.4.2) означает, что для по- |
||||||
÷òè âñåõ x X функция f(x, y) (как функция от y) интегрируема на Y ïî ìåðå |
|||||||
ν è |
∫ f(x, y)dν (как функция от x) интегрируем на X ïî ìåðå µ; аналогично |
||||||
Y
понимается существование второго повторного интеграла);
(b) повторные интегралы (4.4.2) равны между собой и равны интегралу
∫
f(x, y)d(µ × ν).
X×Y
(2)Если функция f(x, y) неотрицательна и существует хотя бы один из повторных интегралов в (4.4.2), то функция f(x, y) интегрируема на X × Y ïî ìåðå µ × ν (и, таким образом, выполнены утверждения (a) и (b) из (1)).
Интеграл Лебега с точки зрения теории метрических пространств.
1 |
векторным пространством. Определим функцию |
|
Согласно лемме 4.4.13, L (X, µ) является |
||
1 |
||
расстояния d1 между элементами пространства L (X, µ) следующим образом: |
||
d1(f, g) := X∫ |f − g|dµ. |
||
Нетрудно заметить, что, вообще говоря, пространство L1(X, µ) с такой функцией расстояния не является метрическим пространством. А именно, свойство (Metr1) метрических пространств может не выполняться: если f почти всюду равная, но тождественно не равная
нулю функция, то d1(f, 0) = 0, íî f ≠ 0. Рассмотрим факторпространство
L1(X, µ) := L1(X, µ)/N(X, µ)
(см. Ÿ1.2). На интуитивном уровне, элементы пространства L1(X, µ) это интегрируемые на X функции, определенные с точностью до прибавления измеримых почти всюду равных нулю
функций (также на интуитивном уровне также можно сказать, что элементы пространства L1(X, µ) это интегрируемые на X функции, причем две такие функции считаются равными,
если они равны почти всюду). Всякую функцию f L1(X, µ) можно рассматривать как элемент пространства L1(X, µ) (и при этом, по сложившейся традиции, ее обозначают той
же буквой).
Определим функцию расстояния d1 между элементами пространства L1(X, µ) следующим
образом: |
d1(f, g) := ∫ |f − g|dµ. |
(4.4.3) |
X
