теория вероятности 5-9 вопросы

5. Зависимые и независимые события. Произведение событий. Понятие условной вероятности. Теорема умножения вероятностей с доказательством. События А, Б, В... называют зависимыми друг от друга, если вероятность появления хотя бы одного из них изменяется в зависимости от появления или непоявления других событий. Примером зависимых событий являются события, происходящие при отборе единиц из совокупности по схеме невозвращенного шара, когда от появления годного или бракованного изделия при первом испытании зависит вероятность появления годного изделия при втором испытании. События называются независимыми, если вероятности появления каждого из них не зависят от появления или непоявления прочих из них. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А — деталь годная, В — деталь окрашенная, то АВ — деталь годна и окрашена.  Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С — появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то АВС — выпадение «герба» во всех трех испытаниях. Условной вероятностью (РA (В)-усл вер-ть соб В относительно А) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. пример условной вероятности Исходя из классического определения вероятности, формулу РA (В) = Р (АВ) / Р (А) (Р (А) > 0 можно доказать. Это обстоятельство и служит основанием для следующего общего (применимого не только для классической вероятности) определения. Условная вер-ть события В при условии, что событие А уже наступило, по определению, равна РA (В) = Р (АВ) / Р (А) (Р(A)>0). Теорема умножения вероятностей зависимых событий. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р (АВ) = Р (А) РA (В) Доказательство  З а м е ч ан и е. Применив формулу (*) к событию ВА, получим Р (ВА) = Р (В) Рв (А), или, поскольку событие ВА не отличается от события АВ, -> Р(АВ) = Р (В) Рв (А) Сравнивая формулы Р (АВ) = Р (А) РA (В) и Р(АВ) = Р (В) Рв (А), заключаем о справедливости равенства Р (А) Ра (В) = Р (В) Рв (А) С л е д с т в и е. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились: где  явл вероятностью события An, вычисленной в предположении, что события А1,А2,..., Аn — 1 наступили. В частности, для трех событий Р (AВС) = Р (А) РA (В) РAB (С). Порядок, в котором расположены события, может быть выбран любым, т. е. безразлично какое событие считатьпервым, вторым и т. д. Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический. Р е ш е н и е. Вероятность того, что первый валик окажется конусным (событие A), Р (А) = 3 / 10. Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик — конусный, т. е. условная вероятность РA (В) = 7 / 9.  По теореме умножения, искомая вероятность Р (АВ) = Р (А) РA (В) = (3 / 10) * (7 / 9) = 7 / 30. Заметим, что, сохранив обозначения, легко найдем: Р (В) = 7 / 10, РB (А) = 3 / 9, Р (В) РB (А) = 7 / 30, что наглядно иллюстрирует справедливость равенства (***).

6. Формула полной вероятности и формулы Байеса(с доказательством). Приимеры

 

   Пусть имеется полная группа попарно

несовместных событий , , …,  с известными вероятностями , , …, . Событие A может наступить только при появлении одного из событий , i=1,...n, причем известны условные вероятности , , …, . Найти вероятность события A по этим данным позволяет формула полной вероятности: .

 

   Пример 1. Предполагается произвести два выстрела в цель из орудия. Необходимо оценить вероятность события A: «разрушение цели», если вероятности попадания снаряда в цель:

0-снарядов ;  1-снаряда ; 2-снарядов 

и вероятности разрушения цели при попадании в нее 0 снарядов ; 1-го снаряда ;  2-ух снарядов .

Решение: Так как события  образуют полную группу попарно несовместных событий, то вероятность разрушения цели:

.

Пусть теперь событие A может, по-прежнему, наступить с одним из попарно несовместных событий , , …, , образующих полную группу. Пусть в результате  какого-то из испытаний событие A произошло. Возникает вопрос, как изменятся условные вероятности событий , , …, , т.е.  i=1,...n, в результате наступления события A?

Ответ на этот вопрос дают формулы Байеса: , i=1,...n,

где  – полная вероятность события A.

 

   Пример 2. По цели было произведено два выстрела и цель, была поражена. Используя данные предыдущего примера, требуется найти вероятности , ,  получения ровно 0, 1 и 2 попаданий.

 Вероятность полного отсутствия попаданий: .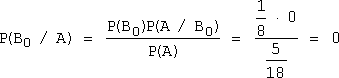

Вероятности одного и двух попаданий:

;  .

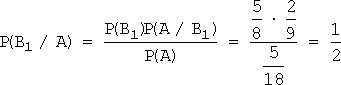Видно, что вероятности событий после разрушения цели изменились, точнее, изменились их условные вероятности, хотя события по-прежнему составляют полную группу.

 

Примеры решения задач на тему «Формула полной вероятности. Формула Байеса»

 

Задача 1. Если р(А) =0,6; р(В) =0,2; р(А/В)=0,7, то чему равна вероятность р(В/А)?

Решение.

По свойству операций над событиями: АВ = ВА, переходя к вероятностям, получим: р(АВ) = р(ВА), используя теорему о вероятности произведения событий, имеем:

р(АВ) = р(А)∙р(В/А) и р(ВА) = р(В)∙р(А/В), отсюда:  р(А) ∙р(В/А) = р(В) ∙р(А/В), тогда:

.

Ответ:       Р(В/А) = 0,2333.

 

Задача 2. Агентство по продаже недвижимости имеет четырех агентов: А, В, С и Д. Агент А беседует с 20%, агент В - с 30%, а агенты С и Д каждый - с 25% обратившихся в агентство клиентов. При этом 70% беседующих с агентом А, 60% беседующих с агентом В, 65% беседующих с агентом С и 80% беседующих с агентом Д совершают сделку.

а) Какова вероятность того, что клиент, обратившийся в агентство, совершит сделку?

б) Клиент, обратившийся в агентство, совершил сделку. Какова вероятность того, что это клиент агента В?

Решение.

Обозначим:

    Е – событие, состоящее в том, что клиент, обратившийся в агентство, совершил сделку;

    А – событие, состоящее в том, что клиент, обратившийся в агентство, беседовал с агентом А;

     В – событие, состоящее в том, что клиент, обратившийся в агентство, беседовал с агентом В;

     С – событие, состоящее в том, что клиент, обратившийся в агентство, беседовал с агентом С;

     D – событие, состоящее в том, что клиент, обратившийся в агентство, беседовал с агентом D.

а) Опишем процесс заключения сделки в событиях: Е=АЕ+ВЕ+СЕ+DE, соответственно:

Р(Е) = Р(АЕ + ВЕ + СЕ + DE) = Р(АЕ) + Р(ВЕ) + Р(СЕ) + Р(DE) = Р(А)∙Р(Е/А) + Р(В)∙Р(Е/В) + Р(С) ∙Р(Е/С) + Р(D) ∙Р(Е/D),

т.к. события АЕ, ВЕ, СЕ и DE – несовместные. 

Но: Р(А)=0,2; Р(В)=0,3; Р(С)=0,25 и Р(D)= 0,25;

Р(Е/А)=0,7;Р(Е/В)=0,6;Р(Е/С)=0,65 и Р(Е/D)=0,8;

Получим: Р(Е)=0,2∙0,7+0,3∙0,6+0,25∙0,65+ 0,25∙0,8=0,6825.

б) Поскольку события А, В, С, D – гипотезы развития процесса Е, то используя формулу Байеса, получим:           .

Ответ:  а) Р(Е) = 0,6825;   б) Р(В/Е) = 0,2637.

 

7. Повторные независимые испытания. Схема и формула Бернулли (с выводом). Примеры.

Определение повторных независимых испытаний. Формулы Бернулли для вычисления вероятности и наивероятнейшего числа. Асимптотические формулы для формулы Бернулли (локальная и интегральная, теоремы Лапласа). Использование интегральной теоремы. Формула Пуассона, для маловероятных случайных событий. Повторные независимые испытания

На практике приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие . При этом интерес представляет исход не каждого "отдельного испытания, а общее количество появлений события  в результате определенного количества испытаний. В подобных задачах нужно уметь определять вероятность любого числа  появлений события  в результате  испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события  в каждом испытании постоянна. Такие испытания называются повторными независимыми.

Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих партиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом.

Формула Бернулли

Воспользуемся понятием сложного события, под которым подразумевается совмещение нескольких элементарных событий, состоящих в появлении или непоявлении события  в –м испытании. Пусть проводится  независимых испытаний, в каждом из которых событие  может либо появиться с вероятностью , либо не появиться с вероятностью . Рассмотрим событие , состоящее в том, что событие  в этих  испытаниях наступит ровно  раз и, следовательно, не наступит ровно  раз. Обозначим  появление события , a  — непоявление события  в –м испытании. В силу постоянства условий испытания имеем

Событие  может появиться  раз в разных последовательностях или комбинациях, чередуясь с противоположным событием . Число возможных комбинаций такого рода равно числу сочетаний из  элементов по , т. е. . Следовательно, событие  можно представить в виде суммы сложных несовместных между собой событий, причем число слагаемых равно :

где в каждое произведение событие  входит  раз, а  —  раз.

Вероятность каждого сложного события, входящего в формулу (3.1), по теореме умножения вероятностей для независимых событий равна . Так как общее количество таких событий равно , то, используя теорему сложения вероятностей для несовместных событий, получаем вероятность события  (обозначим ее )

Формулу (3.2) называют формулой Бернулли, а повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятностей появления в каждом из них события , называют испытаниями Бернулли, или схемой Бернулли.

Пример 1. Вероятность выхода за границы поля допуска при обработке деталей на токарном станке равна 0,07. Определить вероятность того, что из пяти наудачу отобранных в течение смены деталей у одной размеры диаметра не соответствуют заданному допуску.

Решение. Условие задачи удовлетворяет требования схемы Бернулли. Поэтому, полагая , по формуле (3.2) получаем

8. Локальная теорема Муавра-Лапласа, условия её приемлемости, свойство её функции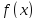.Пример.

Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность Р_{m, n} того, что в n независимых испытаниях событие А наступит m раз, находится по формуле

Р_m, n @ f(x) (4)

где x = (q = 1 – p)

а функция f(x) определяется равенством

f(x) =  (5)

Формула (4) называется локальной формулой Муавра-Лапласа. С возрастание n относительная точность значений вероятностей Р, получаемых по ней, возрастает. Значения функции f(x), заданной формулой (5), находят по таблице. Следует также иметь в виду:

1. Функция f(x) является четной, т.е. f(–x) = f(x). Поэтому в таблице приведены значения функции (5) лишь для положительных значений аргумента.

2. Функция f(x) монотонно убывает при положительных значениях x, а предел ее при x ® ¥ равен нулю.

3. Если x > 5, то можно считать приближенно, что f(x) = 0.

 

Локальная теорема Муавра-Лапласа.

Задача:

Среди телевизоров, поступающих в продажу, 85 % не имеют скрытых дефектов. Какова вероятность того, что в партии из 192 телевизоров будет 150 штук без дефектов?

Решение.

По статистическому определению вероятности, можно считать вероятность того, что случайно выбранный телевизор не имеет скрытых дефектов, равной р = 0,85. Тогда вероятность того, что в партии из n = 192 аппаратов первосортных окажется ровно m = 150, будет определяться по формуле Бернулли:

,

Где  – вероятность того, что телевизор имеет скрытый дефект.

Однако в данном случае из-за больших значений n и m вычисления получаются очень сложными. Для упрощения вычислений используем приближённую формулу.

Так как  больше 10, то применим локальную теорему Муавра-Лапласа:

,

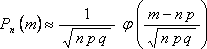Где  – плотность распределения нормированной нормальной случайной величины.

Подставляя данные задачи, получим:

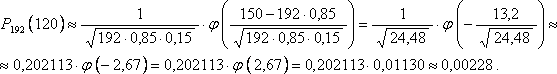
Ответ: вероятность того, что в партии из 192 телевизоров будет 150 штук без дефектов, равна 0,00228.

9. Асимптотическая формула Пуассона и условия ее применимости

Вычисление вероятности P_m,n появления события A при большом числе испытаний п по формуле Бернулли затруднительно. Возникает вопрос о нахождении формул, с помощью которых вероятность P_m,n можно вычислить приближенно. Такие формулы называют асимптотическими. Наиболее простой из них является формула Пуассона.

Теорема(теорема Пуассона). Если вероятность р наступления события A в каждом испытании стремится к нулю при неограниченном увеличении числа испытаний п, причем произведение np стремится к постоянному числу l,то вероятность P_m,n того, что событие А наступит m раз в п независимых повторных испытаниях, приближенно равна

, где l=np .

Доказательство. По формуле Бернулли . При достаточно больших значениях п имеем .

Тогда, 

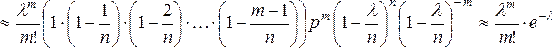, так как

,

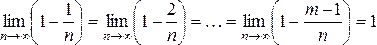 и .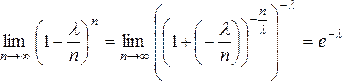

Теорема доказана.

Условия применения:

п – велико, р – мало, так что пр£10;

 пример. Автобиография писателя издается тиражом в 1000 экземпляров. Для каждой книги вероятность быть неправильно сброшюрованной равна 0,002. Найти вероятность того, что тираж содержать ровно 7 бракованных книг.

Решение. Проверим выполнение условия теоремы Пуассона. Для входных значений

получим

что условия выполняются.  По табличным значениям функции Пуассона находим вероятность