Определение. Математическим ожиданием дсв х с законом распределения вероятностей

	х1	х2	…
	р1	р2	…

называется число .В случае бесконечного закона распределения будем предполагать, что записанный ряд сходится. Математическое ожидание случайной величины характеризует ее средневзвешенное значение.

Свойство 1. Если все возможные значения ДСВ Х удовлетворяют неравенству то

Свойство 2. Математические ожидание постоянной величины равно самой этой постоянной, т.е. М(С)=С.

Свойство 3 . Для случайной величины Х и числа Свыполняется М(СХ)=СМ(Х).

Определение.Произведением (суммой) случайных величин Х и с законами распределения вероятностей

	Х1	х2	…	и		y1	y2	…
	Р1	р2	…					…

называется случайная величина, принимающая всевозможные значения (или с вероятностями, равными вероятностям совместного появления значений и .

Определение. Случайные величины Х и Y называется независимыми, если закон распределения каждой из этих величин не зависит от того, какое значение приняла вторая величина.

Свойство 4. Если Х и Y независимые величины, то M(XY) = M(X)M(Y).

Свойство 5. Для случайных величин Х и Y верно равенство M(X+Y)=M(X)+M(Y).

Следствие.Математическое ожидание биномиальной случайной величины Х с параметрами n и p равно M(X)=n p.

Определение. Дисперсиейслучайной величины Х называется математическое ожидание квадрата отклонения этой величины относительно ее математического ожидания.

Дисперсия обозначается через D(X): D(X) = M (( X- M (X))²).

Дисперсия как раз и характеризует средневзвешенное отклонения в квадрате значений величины относительно ее математического ожидания. Несложно получить и другую более удобную формулу для нахождения дисперсии: D(X)=M(X²)-M(X)².

Определение. Средним квадратическим отклонением называется . Обозначается , т.е. .

Перечислим основные свойства дисперсии.

Свойство 1. Дисперсия случайной величины Х неотрицательна: .

Это следует из того, что квадрат отклонения случайной величине не отрицателен.

Свойство 2. Дисперсия ДСB Х равна нулю только в том случае, когда Х - постоянная.

Свойство 3. Если X -ДCB, а С число, то D(CX )= C²D(X).

Свойство 4. Дисперсия суммы независимых величин равна сумме их дисперсии

.

Свойство 5. Для независимых величин X и Y: D(X-Y)=D(X)+D(Y).

Следствие. Дисперсия биномиальной случайной величины Х с параметрами n, p равна

.

Осн.лит: 19 [7-62], 21 [8-58],

Контрольные вопросы:

1. Сформулируйте теоремы сложения и умножения вероятностей зависимых и независимых

2. Приведите формулы полной вероятности и Байеса.

3. Приведите формулы Бернулли, Муавра-Лапласа(локальной и интегральной), Пуассона.

4. Перечислите свойства числовых характеристик ДСВ.

Лекция 14. Непрерывная случайная величины (НСВ) и ее числовые характеристики НСВ. Нормальный, равномерный и показательный законы распределения. Закон больших чисел

Определение. Случайная величинаХ, функция распределения которой непрерывна для всех ,называется непрерывной случайной величиной.

Примеры:Время ожидания транспорта на остановке, время горения электрической лампочки.

Определение. Плотностью распределения вероятностей непрерывной случайной величиныХназывается производная ее функции распределения: .

Перечислим основные свойстваплотности вероятности непрерывной величины.

Свойство 1. Плотность случайной величины Х неотрицательна:.

Это свойство следует из того, что - неубывающая функция.

Свойство 2. Для любого отрезка вероятность попадания значения величины в этот отрезок равна интегралу от плотности случайной величины по этому отрезку:

Свойство 3.Для непрерывной величины с плотностью верно.

Свойство 4 (формула обращения) Если плотность непрерывной величины , то ее функция распределения вероятностей равна .

Определение. Математическим ожиданиемнепрерывной случайной величины Х с плотностью называется число Если все значения лежат в отрезке , то мат. ожидание равно. Предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл. Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к, а верхнего к. По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Определение. Дисперсиейнепрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения принадлежат отрезку, то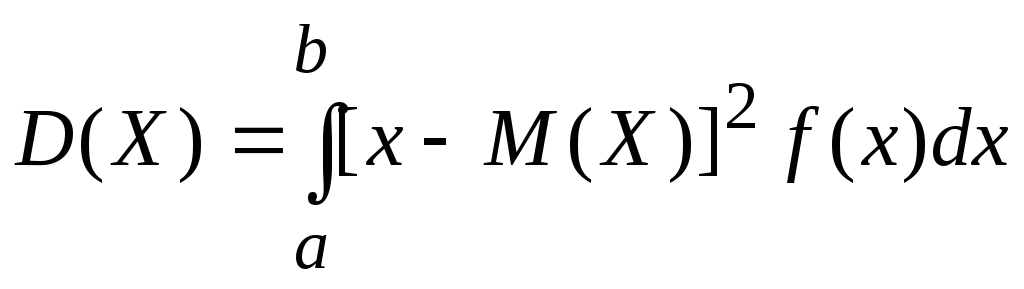; если возможные значенияпринадлежат всей оси, то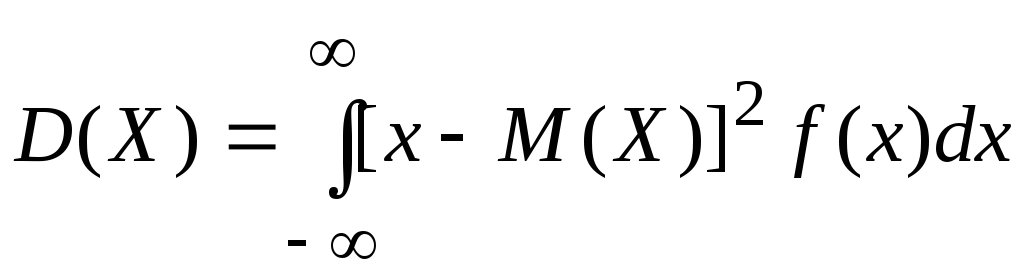. Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством.

Пример.Найти математическое ожидание и дисперсию случайной величины, заданной интегральной функцией

Решение.Найдем дифференциальную функцию

Найдем математическое ожидание .

Найдем дисперсию .

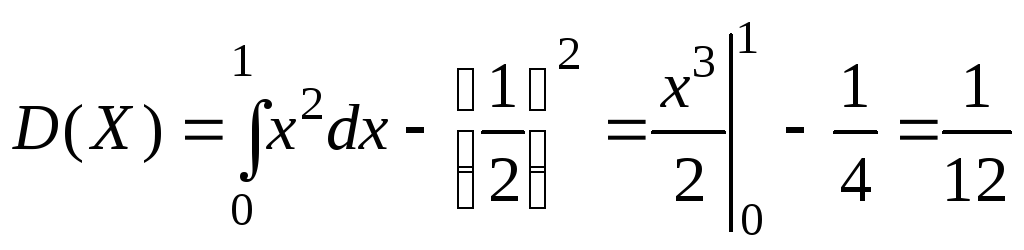Определение. Нормальным называют распределение вероятностей непрерывной случайной величины, если диф­ференциальная функция (плотность вероятности) определяется равенством

.

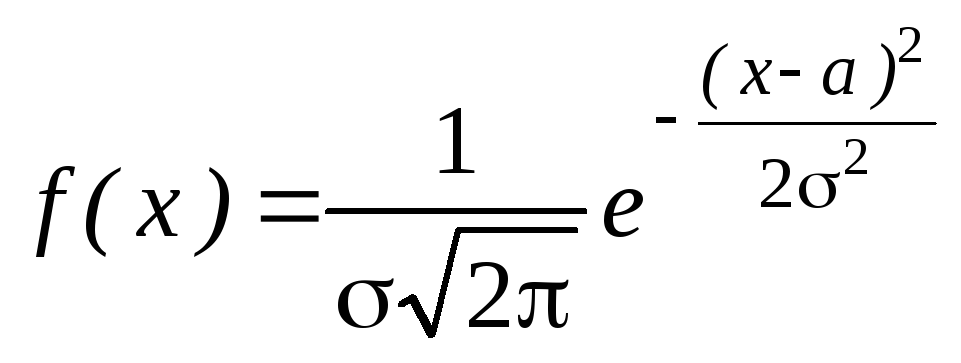Мы видим, что нормальное распределениеопределяется двумя парамет­рами:и. Достаточно задать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков:есть математическое ожидание,среднее квадратическое отклонение нор­мального распределения.

а) По определению математического ожидания непрерывной случайной величины

.

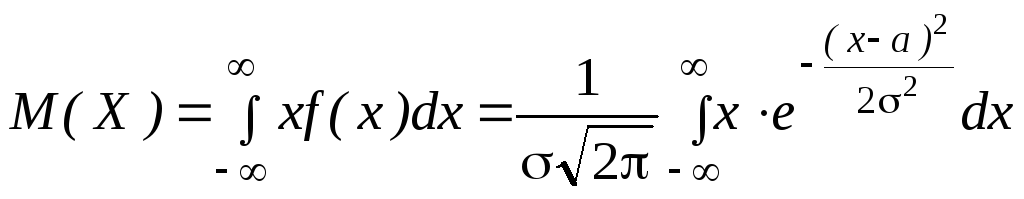Итак, , т.е. математическое ожидание нормального распределения равно параметру.

б) По определению дисперсии непрерывной случайной величины, учитывая, что , имеем 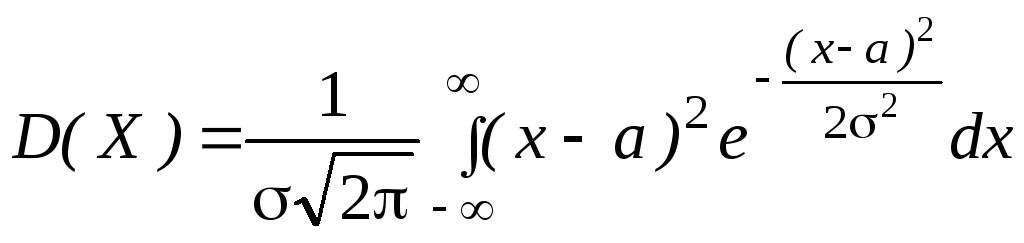. Введем новую переменную. Отсюда ,. Приняв во внимание, что новые пределы интегрирования равны старым, получим . Интегрируя по частям, положив,, найдем. Следовательно,.Итак, среднее квадратическое отклонение нормального распределения равно параметру .

Известно, что, если случайная величина задана дифференциальной функцией , то вероятность того, что примет значение, принадлежащее интервалу ,равна .Пусть случайная величина распределена по нормаль­ному закону. Тогда вероятность того, что примет значе­ние, принадлежащее интервалу , равна

.

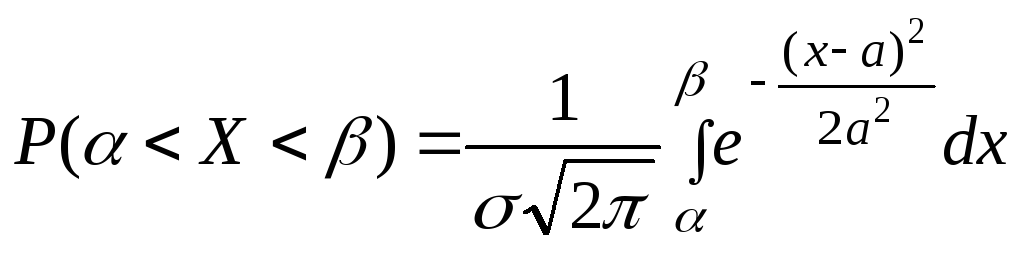Преобразуем эту формулу так, чтобы можно было поль­зоваться готовыми таблицами. Введем новую переменную . Отсюда,. Найдем новые пределы интегрирования. Если, то; если , то. Таким образом, имеем

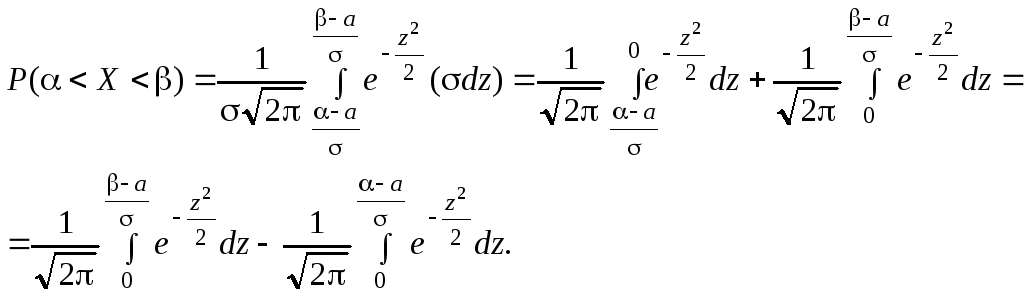
Пользуясь функцией Лапласа ,

окончательно получим (*)

Часто требуется вычислить вероятность того, что от­клонение нормально распределенной случайной величины по абсолютной величине меньше заданного положитель­ного числа , т.е. требуется найти вероятность осуще­ствления неравенства . Заменим это равенство равносильным ему двойным неравенством , или .Пользуясь формулой (*), получим

.

Приняв во внимание равенство (функция Лапласа – нечетная), имеем

.В частности, при.Преобразуем полученную формулу положив. В итоге получим.

Если и, следовательно,, то,т.е. вероятность того, что отклонение по абсолютной вели­чине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозмож­ности маловероятных событий, можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического оживания не превосходит утроенного среднего квадратичес­кого отклонения.

На практике правило трех сигм применяется так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то имеются основания предполагать, что изучаемая вели­чина распределена нормально; в противном случае она не распределена нормально.

Закон равномерного распределения вероятностей. Показательное распределение

Определение. Распределение вероятностей называют равномерным, если на интерва­ле, которому принадлежат все возможные значения случайной величины, плотность вероятности имеет постоянное значение. Найдем дифференциальную функцию равномерного распределения, считая, что все возможные значения случайной величины заключены в интервале , на котором дифференциальная функция сохраняет постоянное значение . По условию X не принимает значений вне интервала , поэтому при и. Найдем значение постоянной С. Так как все возможные значения случайной величины принадлежат интервалу , то должно выполняться равенство

или Отсюда

Итак, закон равномерного распределения аналитически можно записать так:

Определение.Показательной случайной величиной с параметрамназывается случайная величина,имеющая плотность вероятности вида

Несложно проверить, что т.е. что определение данной плотности корректно.

Числовые характеристики показательно распределенной величины равны:

и .

Под законом больших чиселв теории вероятностей понимается набор теорем, описывающих поведение суммы большого числа случайных величин. При выполнении некоторых условий, эта сумма обладает свойствами практически не зависящими от свойств слагаемых , а часто эта сумма теряет свойства случайности и приближается к постоянной.

Теорема (Неравенство Чебышева). Пусть Х – случайная величина, М() ее математическое ожидание, D() – дисперсия,-число. Тогда.

Теорема Чебышева. Пусть- последовательность независимых случайных величин, дисперсии которых ограничены некоторым числом, т.е.для всех.

Пусть , .

Тогда для любого верно соотношение

Смысл этой теоремы состоит в том, что при выполнении ее условий вероятность отклонения среднего арифметического случайных величин от среднего арифметического их мат. ожиданий меньше чем на любое малое число стремится к единице с ростом.

Определение. Пусть имеется последовательность случайных величин. Эта последовательность называется сходящейся по вероятности к числу,если для каждого верно .Соответствующее обозначение

Это определение позволяет использовать понятие предела в теории вероятностей.

Следствие. Пустьпоследовательность независимых величин с равными мат. ожиданиямии ограниченными числом С дисперсиями, тогда последовательность их средних арифметических присходится по вероятности к мат. ожиданию, т.е..

Теорема Бернулли. Пусть имеется последовательность испытаний, в каждом из которых событиямогут появляться с вероятностью, пусть - относительные частоты появления событий виспытаниях, тогдапристремится кпо вероятности, т.е.

Осн. лит: 19 [67-92],[105-117], [121-150], 21 [99-131] [148-161]

Контрольные вопросы

1. Числовые характеристики Н.С.В и их свойства.

2. Что понимают под законом больших чисел.

3. Сформулируйте неравенство и теорему Чебышева.

4. Сформулируйте теорему Бернулли.

5. Опишите нормально распределенную случайную величину и ее характеристики.

Лекция 15. Элементы математической статистики . Генеральная и выборочная совокупности. Полигон. Гистограмма. Статистическая гипотеза. Доверительный интервал.

Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Определение. Выборочной совокупностью, или простовыборкойна­зывают совокупность случайно отобранных объектов. Генеральной совокупностьюназывают совокупность объектов, из которых производится выборка. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 де­талей, то объем генеральной совокупности, а объем выборки.

Пусть из генеральной совокупности извлечена выборка, причем наблюдалосьраз,-раз,-раз и- объем выборки.

Определение. Наблюдаемые значенияназывают вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки- относительными частотами.

Определение. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

Пусть известно статистическое распределение частот количественного признака . Введем обозначения:- число наблюдений, при которых наблюдалось значе­ние признака меньшее,- общее число наблюдений (объем выборки). В целях наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.Полигоном частотназывают ломаную, отрезки которой соединяют точки,,...,.Полигоном относительных частотназывают ломаную, отрезки которой соединяют точки,,...,.

В случае непрерывного признака целесообразно строить гистограмму. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат частичные интервалы длиною, а высоты равны отношению(плотность частоты).

Статистические оценки выборочных характеристик.

Любые характеристики СВ определяются ее законом распределения, поэтому одна из основных задач математической статистики(МС) – по наблюдениям над независимыми реализациями СВ т.е. по выборке определить приближенные значения параметров распределения. Вместо слова “ приближенное значение “ в МС используется термин “оценки” параметров.

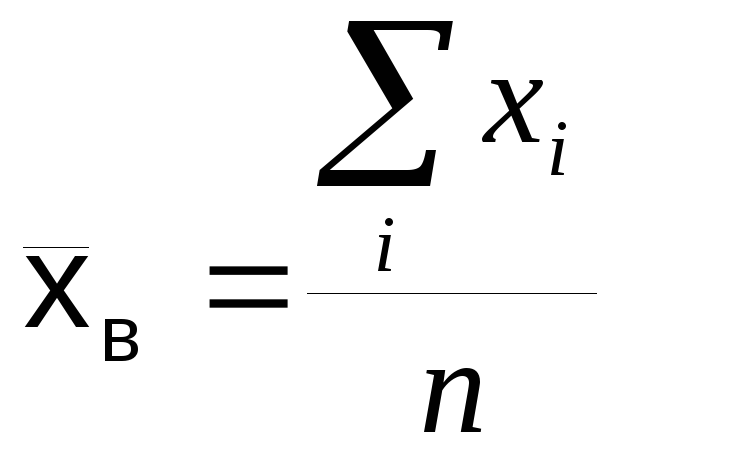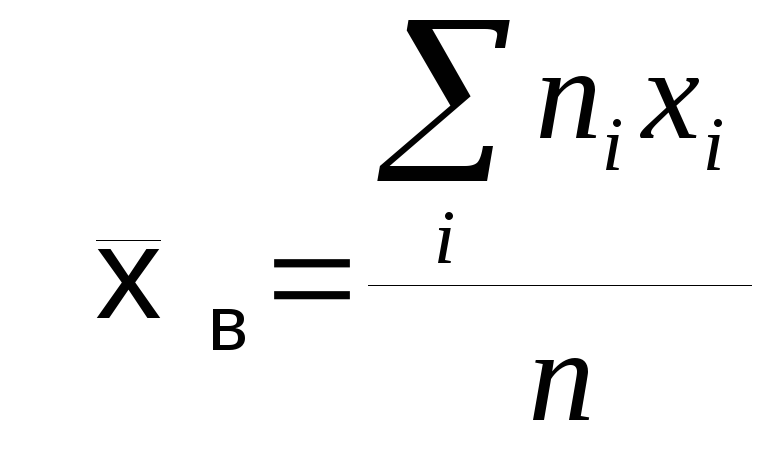Определение: Выборочным средним или выборочным аналогом математического ожидания называется величина, если все значенияx_iразличны, , если значения x_i повторяются с соответствующими частотамиn_i .

Определение:Выборочной дисперсиейили выборочным аналогом дисперсии называется величина, если все значенияx_iразличны ;, если значения x_i повторяются с соответствующими частотамиn_i .

Определение:Выборочным среднеквадратичным отклонениемназывают величину: если значения x_i повторяются с соответствующими частотамиn_i .

Вместо выборочной оценки дисперсии чаще всего используют следующую оценку-несмещенная оценка дисперсии. Для одних и тех же параметров можно использовать разные оценки, которые различаются свойствами. Пусть- оценка характеристики распределения, полученная по выборке объемаn. Тогда оценканазываетсясостоятельной,если-→по вероятности, когдаn→∞ ( P(=)→1 при (n→∞), оценканазываетсянесмещенной, если М=, оценканазываетсяэффективной, если некоторая функция ее отклонения от значенияминимальна ( например, дисперсия).

Определение: Точечной называется оценка, определяемая одним числом, н-р: выборочная средняя и выборочная дисперсия являются точечными оценками.

Для нахождения точечных оценок обычно применяют метод моментов:

Определение : Начальнымэмпирическим моментомk- го порядка называется среднее значение к – х степеней выборочной совокупности=nx/n. Начальный эмпирический момент первого порядка равен выборочной среднейx.

Центральнымэмпирическим моментом к – го порядка называется среднее значение к –х степеней разностейx-x.Центральный эмпирический момент второго порядка равен выборочной дисперсииD. Основой метода моментов является то, что эмпирические моменты рассматриваются как оценки теоретических моментов распределения случайной величины. Неизвестные параметры теоретического распределения выражаются как функции теоретических моментов. Заменяя теоретические моменты эмпирическими, получим оценки искомых параметров.

Пример: Найти точечную оценку параметрапоказательного распределения:

F(X) =1 –EXP(-x),F(x)=0,приx<0 илиf(x) =exp( -x),f(x)=0,приx<0 по результатам выборки.Теоретический момент первого порядка (математическое ожидание) находится интегрированием:.Эмпирический момент 1-го порядка представляет собой выборочную среднюю. Поэтому

При выборке малого обьема точечная оценка может существенно отличаться от оцениваемого параметра. В этом случае,обычно пользуются интервальными оценками.

Доверительная вероятность. Доверительный интервал

Оценка, определяемая двумя числами - концами интервалов, называется интервальной.

Пусть - оценка неизвестного параметра , полученная поданным выборки. Очевидно, оценка тем точнее, чем меньше модуль разности . Если и ,то чем меньше , тем точ­нее оценка ; число характеризует точность оценки.

Определение. Доверительной вероятностью, или надежностью, оценки а параметра называется вероятность , с которой осуществляется неравенство т.е. (1). Обычно надежность задается заранее, в качестве берут число, близкое к единице. Так как неравенство равносильно неравенствам или ,то формулу (1) можно записать в виде (2)

Эта формула означает следующее: вероятность того, что интервал заключает в себе (покрывает) неизвестный параметр ,равна .

Определение. Интервал , который покрывает неизвестный параметр с заданной надежностью , называется доверительным интервалом. Концы доверительного интервала называют доверитель­ными границами. Доверительные границы являются случайными величинами (они изменяются от выборки к выборке). Рассмотрим вопрос о построении доверительного интервала для оценки математического ожидания а нормального распределения при известном значении среднего квадратического отклонения . Пусть количественный признак X генеральной совокупности имеет нормальное распределение с заданным и неизвестным а. Оценим неизвестный параметр а выборочной средней ; найдем доверительный интервал, покрывающий параметр а с надежностью .Так как выборочное среднее меняется от выборки к выборке, его можно рассматривать как случайную величину Х_В.. Выборочные значения х₁,,х₂,,...,х_п также меняются от выборки к выборке. Будем рассматривать их, как одинаково распределенные случайные величины Х₁,Х₂,,...Х_п (математическое ожидание каждой из этих величин равно а, среднее квадратическое отклонение равно ). Имеем , (3). Потребуем, чтобы (4)

Поскольку случайная величина Х_В. также имеет нормальное распре­деление, то равенство

_, применяя к величинам Х_В. и , находим

(5), где (6)

Из последнего равенства определим и подставим в (5):

Статистические гипотезы.При статистических исследованиях приходится на основе предварительного анализа выдвигать гипотезы о виде закона распределения СВ или о параметрах этого закона.Такие гипотезы называются статистическими.После сбора и обработки статистической информации указанные гипотезы могут быть проверены.Нулевой( основной) называют выдвинутую гипотезу Н .КонкурирующейХ(альтернативной) называют гипотезу Н1,которая противоречит основной. Например: Н0: М()=5,H1:M(X)#5. В результате проверки статистической гипотезы на основе статистической информации могут возникнуть ошибки двух родов. Ошибка первого рода состоит в том,что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том,что будет принята неправильная гипотеза. Для проверки нулевой гипотезы вводят в рассмотрение специально подобранную СВ –статистический критерий( К) ,распределение которой известно.и которая обеспечивает малое значение допустимой вероятность ошибки первого рода.

Множество значений этого критерия (статистики) можно разделить на два непересекающихся подмножества: 1) область принятия гипотезы(допустимая область), 2)подмножество значений, при которых гипотеза Н0 отвергается и принимается альтернативная гипотеза Н1,называемое критической областью. Граничные точки критических областей определяют по таблицам распределения выбранного критерия. Различают левостороннюю, правостороннюю и двустороннюю критические области. Например:Н0:M(X)=x,H1:M(X)x– двусторонняя критическая область илиH1:M(X)>x– правосторонняя критическая область. Вернемся к предыдущему примеру: построение доверительного интервала для оценки математического ожидания при известной дисперсии.

Пример:Пусть х;=5,n=4,D=1,уровень надежности=0,954.

Ф( x-<M(X)<x+)=/2=0,477. По таблице найдем соответствующее значениеz=2,=1

Доверительный интервал (5-1,5+1) =(4,6),Следовательно, 4<M<6 с вероятность0,954

Рассмотрим эту же задачу в следующей постановке: выдвигаем гипотезу о равенстве математического ожидания рассматриваемого экономического показателя выборочному среднему, вычисленному по выборке Н0: M(X)=x_в,при этом ошибка первого рода (уровень значимости) равна 1 – 0,954 =0,0466.Для проверки введем статистическийZ–критерий:Z=(M(X)-xв)n/.Распространены 4 критерия:1)Z- критерий,2)Стьюдента,3)хи – квадрат, ,4) Фишера. Распределения этих критериев рассчитаны, табулированы и могут быть использованы для проверки гипотез следующим образом: :задается уровень значимости (значение ошибки 1 рода),т.е. вероятность того что соответствующая СВ попадет в критическую область, выходящую за интервал принятия гипотезы (К1,К2).С учетоми известного числа степеней свободы из соответствующих таблиц находят значения критерия для определения границ критической области. Затем, используя статистические данные, подсчитывают значения соответствующего критерия и сравнивают с К критическим (из таблицы) Если К вычисленное > К критического,(т.е. попадает в критическую область), то нулевая гипотеза отвергается, если К выч. < К крит.,то она принимается.

Осн.лит.: 19, глава 15,16 [185-228]; глава 19[282-290]

Контрольные вопросы:

1. Дайте определение выборочному математическому ожиданию.

2. Дайте определение выборочной дисперсии;

3. Опишите различие точной и интервальной оценок.

4. Какие гипотезы называются статистическими?