1. Линейные дифференциальные уравнения -го порядка

Определение.Уравнение вида

, (18)

где ,;,называется линейным дифференциальным уравнением (далее - ЛДУ) -го порядка. Функцияназывается правой частью уравнения (18), функции- коэффициентами ЛДУ (18).

Если , то уравнение

(19)

называетсяоднородным ЛДУ -го порядка. Уравнение (18) с ненулевой правой частью называют неоднородным ЛДУ. Дифференциальные уравнения (18) разделяют на два вида:

1) ЛДУ с переменными коэффициентами.

2) Если все эти функции являются постоянными величинами, то такое ЛДУ называется уравнением с постоянными коэффициентами. Оно имеет вид

.

2. Линейный дифференциальный оператор и его свойства

Определение.Линейным дифференциальным оператором -го порядка назовем выражение

Тогда линейные дифференциальные уравнения (18), (19) с учетом линейного дифференциального оператора можно переписать в сокращенном виде ,. Перечислим свойства этого оператора: 1) Постоянный множитель можно вносить за знак линейного дифференциального оператора. 2) Линейный дифференциальный оператор от сумм конечного числа функций равен сумме линейных дифференциальных операторов слагаемых

.

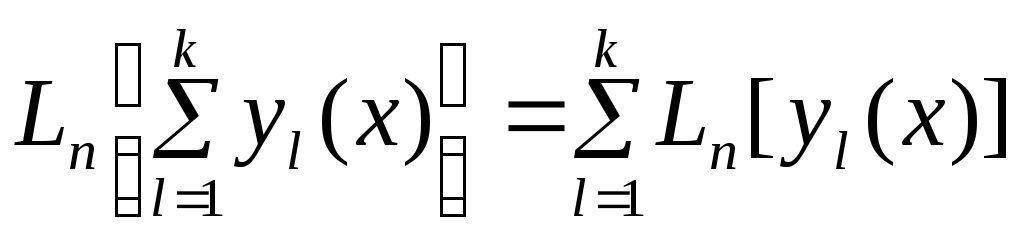3. Однородные линейные дифференциальные уравнения

Рассмотрим однородное ЛДУ ,, (20)

причем . Однородное ЛДУ (ОЛДУ) обладает следующими свойствами.

1) Если является решением ОЛДУ (20), то функциятакже является решением этого уравнения. 2) Еслииявляются решениями однородного ЛДУ (20), то их сумма также является решением уравнения (20). 3) Если функцийявляются частными решениями однородного ЛДУ (20), то их линейная комбинациятакже является решением уравнения (20).

4. Линейная независимость функций

Определение.Функции называются линейно независимыми на , если соотношение(21)

выполняется только при всех (т.е. если это соотношение не выполняется для отличных от нуля чисел).

Определение.Система функцийназывается линейно зависимой на , если существует числа, не все равные нулю, такие, что выполняется соотношение (21).

Примеры:1. Функции,линейно зависимы, т.к.,,.

2. Функции ,,,линейно независимы.

Определение. Функциональный определитель вида

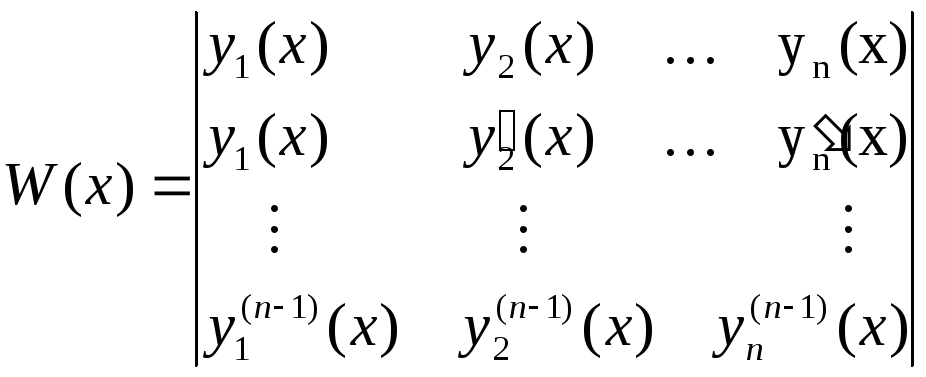
называется определителем Вронского -го порядка (вронскианом -го порядка).

Теорема (необходимое условие линейной зависимости). Если система функцийлинейно зависима на, то вронскиан, составленный их этих функций, равен нулю.

5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Рассмотрим однородное ЛДУ -го порядка

, (22)

где . Будем искать его решение в виде(23)

где - пока неизвестное постоянное число. Такая замена называется подстановкой Эйлера и используется потому, что при дифференцировании сохраняется ее форма. Для того, чтобы найти неизвестное число, продифференцируемраз:,, …,и подставим в уравнение (22)

.

Вынесем за скобки и сократим на него, так как

. (24)

Относительно неизвестной получили алгебраическое уравнение-ой степени. Уравнение (24) называетсяхарактеристическим уравнениемдля ЛДУ (22). В силу основной теоремы алгебры характеристическое уравнение (24) имеет ровнокорней (различных, кратных, комплексных).

Сформулируем теорему, описывающую общее решение однородного ЛДУ в наиболее часто встречающемся в приложениях случае .

Теорема.Пусть и- корни характеристического уравнения для ЛДУ с постоянными коэффициентами. Тогда возможны три случая:

1) Если и-действительные и различные () - то общее решение ЛДУ есть.

2) Если , то.

3) Если , то.

Рассмотрим теперь методы нахождения частного решения неоднородного ЛДУ.