Осн. лит.: 1, § 5-7, [34-48], § 8-9, [49-71], 12.

Доп. лит.: 6, 25.

Контрольные вопросы:

1. Перечислите основные свойства скалярного и векторного произведений. Расстояние от точки до прямой.

2. Что называется смешанным произведением?

3. Условие параллельности двух прямых.

4. Угол между плоскостью и прямой

5. Условияпараллельностии перпендикулярности плоскостей.

6. Расстояние от точки до плоскости.

Модуль -2. Дифференциальное и интегральное исчисление функций одной переменной

Лекция 4. Введение в анализ. Функция и предел функции. Непрерывность. Основные свойства функций. Пределы. Бесконечно малые функции.

Определение. Функциейfс областью определения D и областью значений Е называется некоторое отображение из D в Е, т. е. соответствие, при котором каждому элементусопоставляется единственный элемент.

Элементы xDназываются значениями аргумента, а элементыyE– значениями функций. МножествоDназывается областью определения функции, множествоEвсех значений функции – областью значений этой функции.

Функция, заданная формулой y=f(х), правая часть которой не содержитy, называется явной функцией. Функцияy=f(х), удовлетворяющая уравнению видаF(x,y(x))=0, называется функцией, заданной неявно, или неявной функцией.

В случае, когда каждому yEпо некоторому закону соответствует только одно значениеxD, получаем функциюx=φ(y), заданную на множествеEсо значениями в множествеD. Функциюx=φ(y) называют обратной функцией по отношению к функцииy=f(х).

Способы задания.

а) Табличный.Функция может быть задана в виде таблицы.

б) Графический. Графиком функцииназывается множество точек (х,у) плоскоститаких, что и. График даёт наглядное представление о характере поведения функции.

в) Аналитический. Аналитическимспособом, т. е. с помощью одной формулы можно задавать только элементарные функции. Это самый универсальный способ задания функции, из которого можно получить и таблицу и график.

Для функции ограниченность означает выполнение неравенствапри всехиз области определения.

Предел функции

Определение. Число А называетсяпределомфункциипри, если для каждогонайдётся такое0, что для всехвыполняется неравенство, т. е..

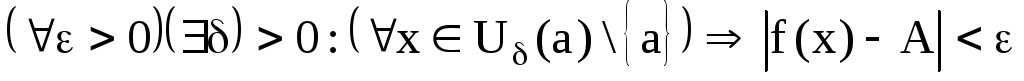Обозначается или. Дадим определения пределов функции при.

Пусть функция определена в некоторой окрестности точкиа, кроме быть может, этой точки (рис. 1).

Определение. Число А называется пределом слева функциипри, если. (Обозначаетсяили).

Определение. Число А называется пределом справа функциипри, если. (Обозначаетсяили).

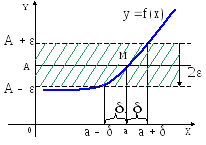
Рис.1

Теорема.существует в том и только в том случае, когда существуют пределы, и они равны между собой.

Пример. .

В этом примере рассматривается только , поэтому.

.

не существует, поскольку.

Определение. Число А называется пределом функциипри, если для каждого0 найдётся такое число N , что при любомвыполняется, т. е.

. (Обозначается).

Определение. Число А называется пределом функциипри, если. (Обозначается.

Определение. Число А называется пределом функциипри, если. (Обозначается).

Теорема. Пределсуществует в том и только в том случае, когда существуюти они равны между собой.

Примеры: (предел существует);

(предел не существует).

Свойства функций, имеющих предел.Рассматриваемые ниже свойства справедливы для всех видов пределов функций. Однако для краткости будем формулировать их для одного предела (при): 1) Предел постоянной функции равен этой постоянной, т.е. . 2) Если предел функции существует, то он единствен.

Бесконечно малые функции

Определение.Функцияназывается бесконечно малой(б. м.) при, еслиили

Пример.Функцияявляется б.м. прии не является таковой при.

Теорема.Пустьб.м. при, аограничена в некоторой окрестности точки а, тогдаявляется б. м. при.

Пример.

Вычислим: .

При величина х является б. м., а функцияограничена, так как. Следовательно, искомый предел, как предел б. м., равен нулю.

Теорема.Пределравен числу А в том и только в том случае, когдаявляется б.м. при.

Пример.означает, чтоявляется б. м. при.

Аналогично при .

Основные теоремы о пределах. Пустьи- функции, для которых существуют пределы при(или при): , . Сформулируем основные теоремы о пределах.

1. Функция не может иметь более одного предела.

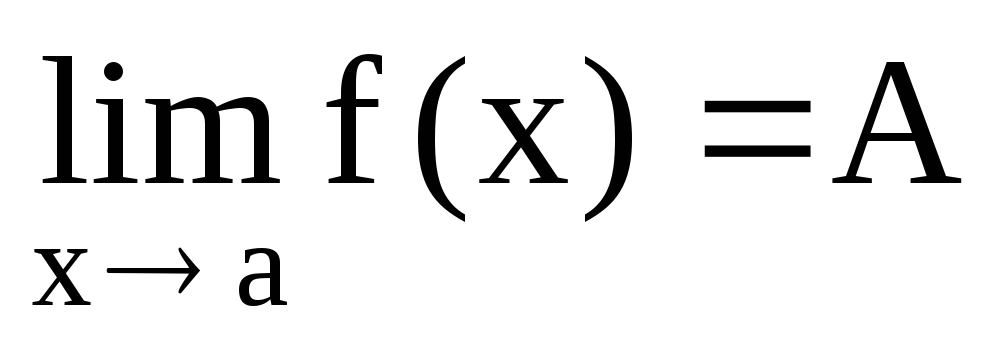2. Если и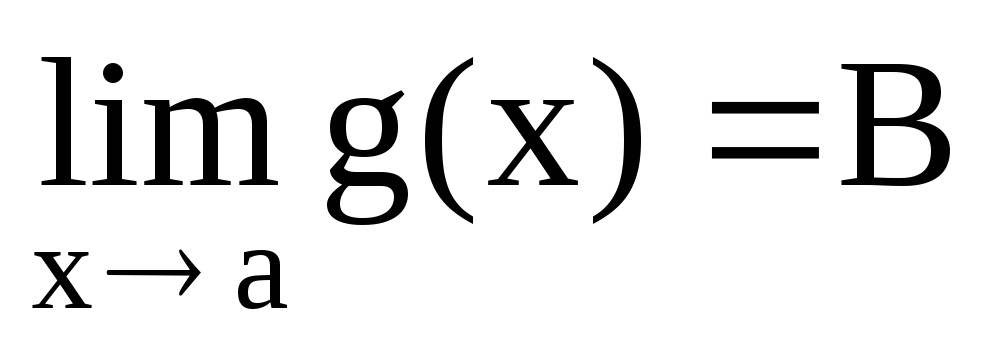,то предел алгебраической суммы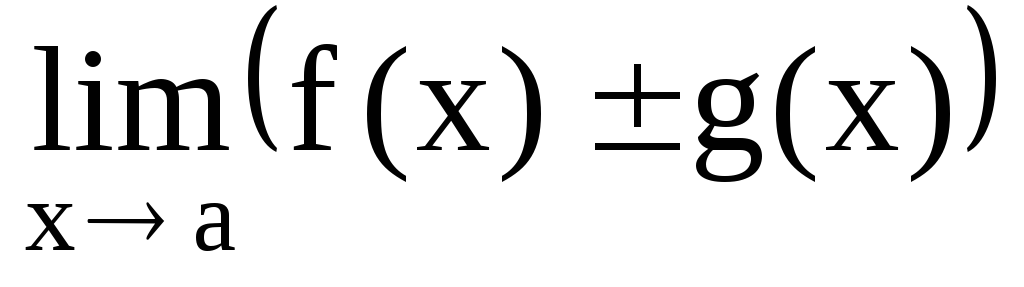существует и равен АВ.

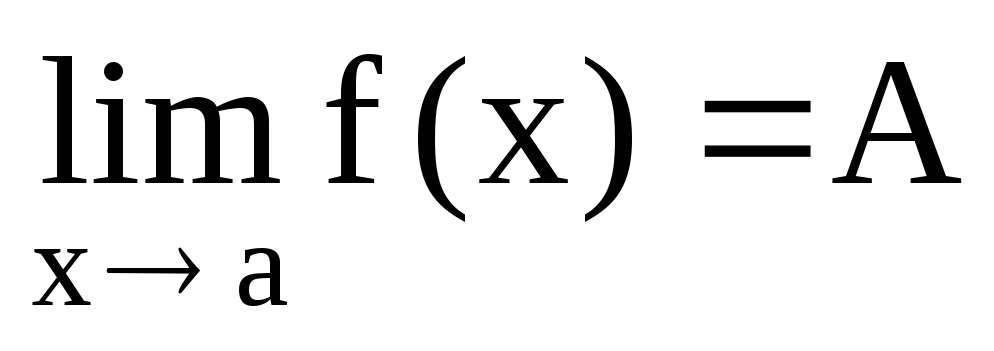3. Если и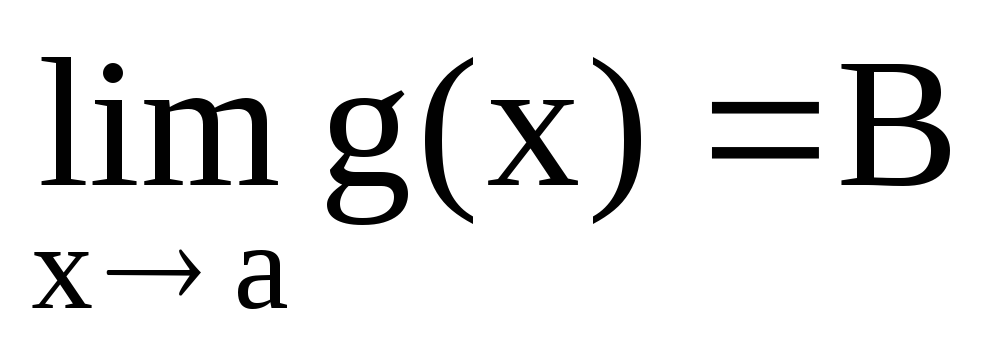, то существует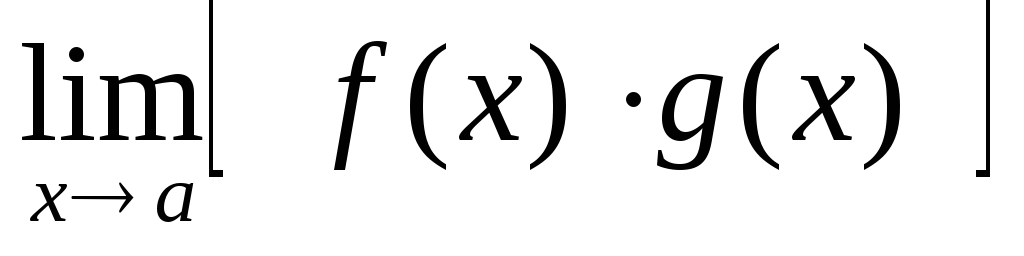и равен.

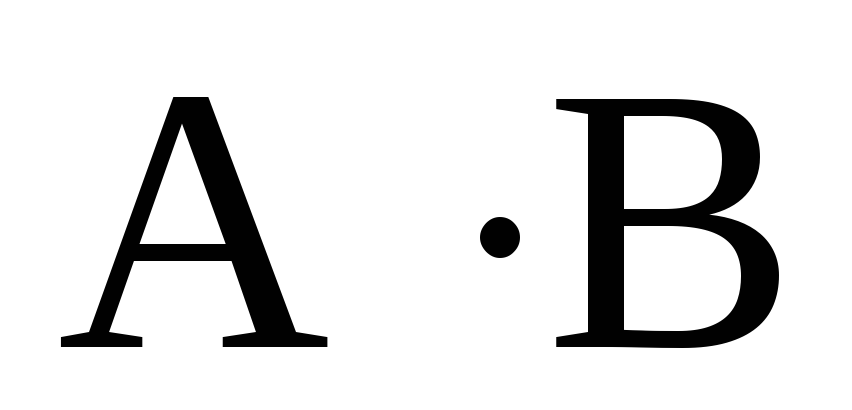4. Если иисуществуют, то существуети равен.

Первый замечательный предел .

Пример. .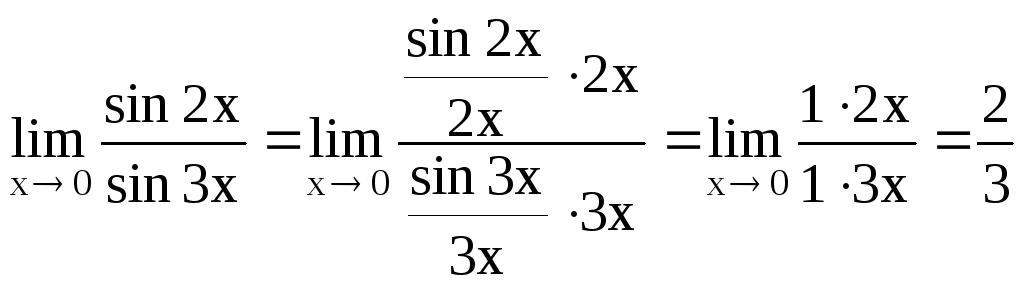

Второй замечательный предел

.

Здесь е  2,718282… – иррациональное число.

Пример.Вычислим предел:

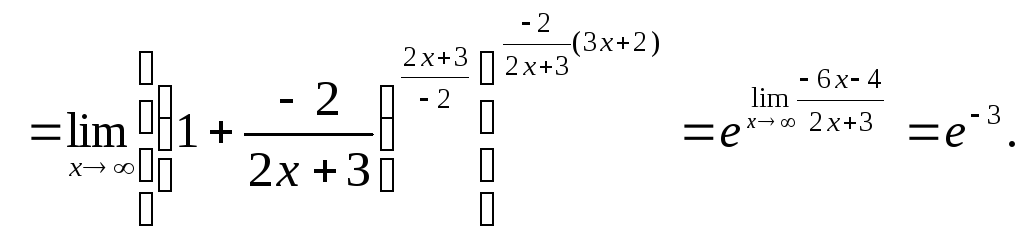
Определение.Бесконечно малыеприназываются эквивалентными, если. Обозначение  .

Это отношение эквивалентности удовлетворяет трём свойствам

1. ;

2. ;

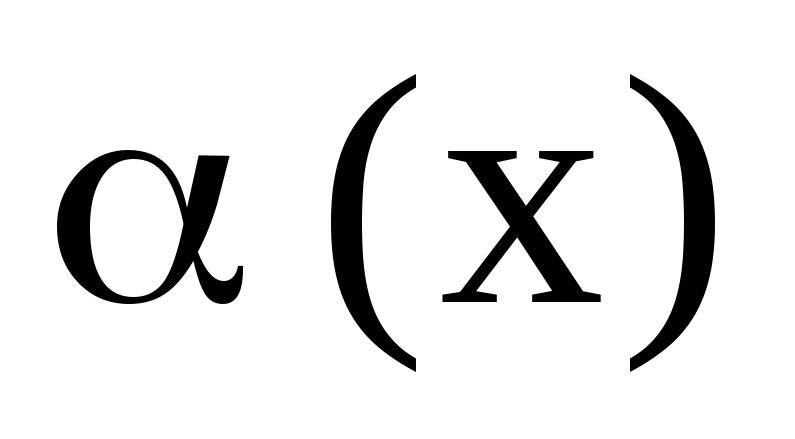
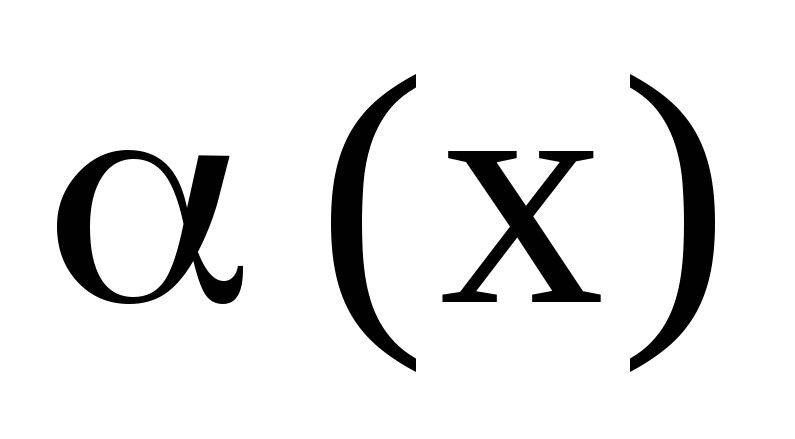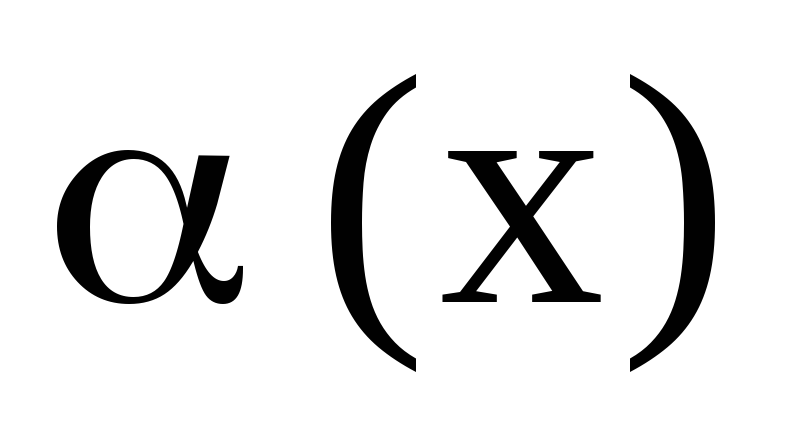
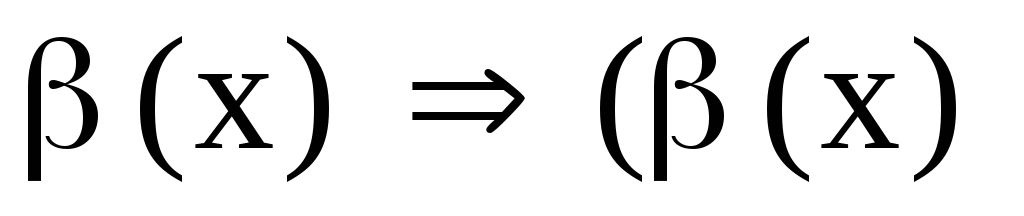
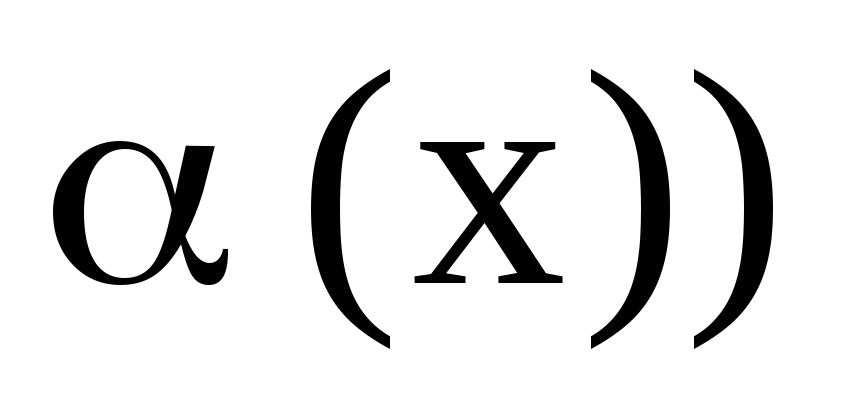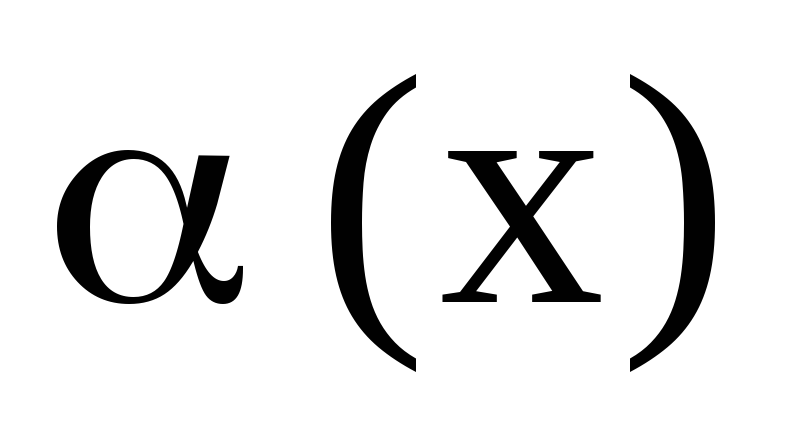
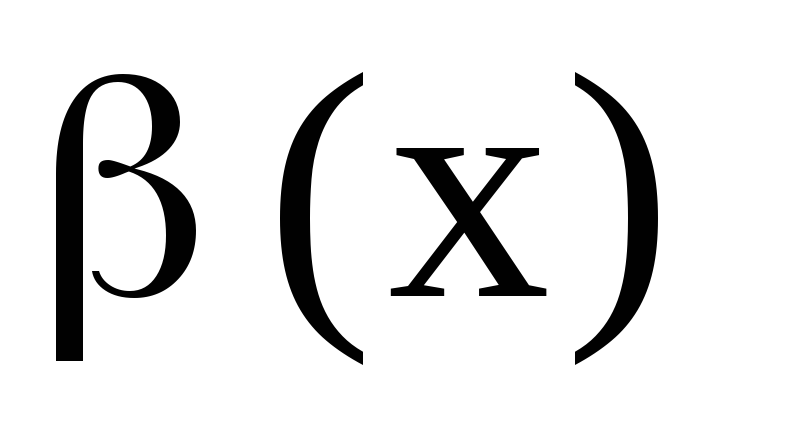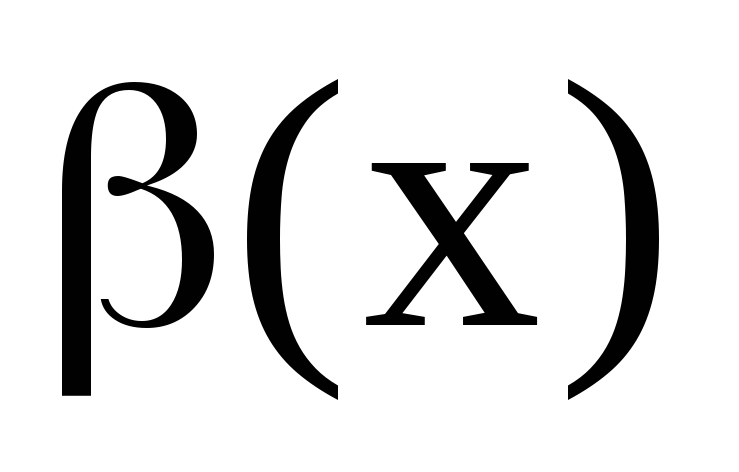
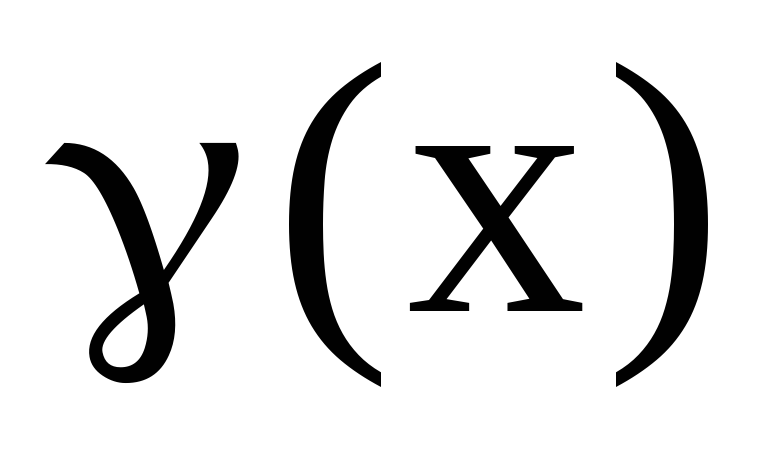3. Если и, то.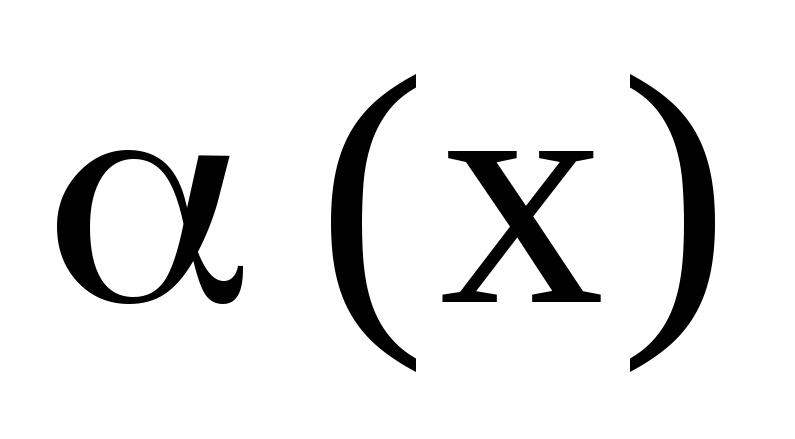

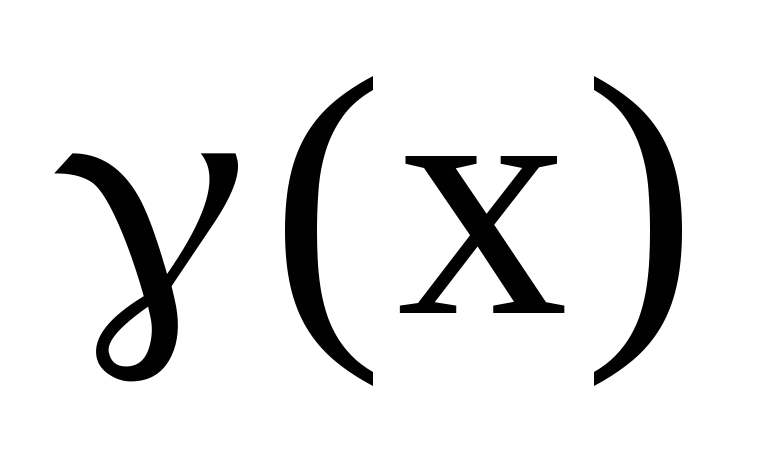Теорема.Пустьесть б. м. при, тогда:

; ; ; ;

; ,; .

Непрерывность функции

Определение.Функцияназываетсянепрерывнойв точке, если выполняются три условия: 1) существует; 2) существует; 3).

Функция называется непрерывной в точкеслева (справа), если выполняются три условия: 1)

2)или

3)или

Очевидно, что функция является непрерывной в точке в том и только в том случае, когда она непрерывна в этой точке слева и справа.

Следствие.Любая элементарная функция непрерывна во всех внутренних точках своей области определения, а в граничных точках отрезков области определения непрерывна справа или слева.