Классификация точек разрыва

Определение.Точка, в которой нарушается хотя бы одно условие непрерывности функции, называется точкой разрыва этой функции.

Рассмотрим точку разрыва функции, в некоторой окрестности которой (кроме быть может) эта функция определена. Возможны три случая:

1. Еслине определена или, тоназывается точкой устранимого разрыва. Если эту функцию изменить в точке, т. е. положить то функциябудет непрерывной в точке, т. е. этот разрыв устраняется.

Пример.Функцияимеет устранимый разрыв в точке. Если положить

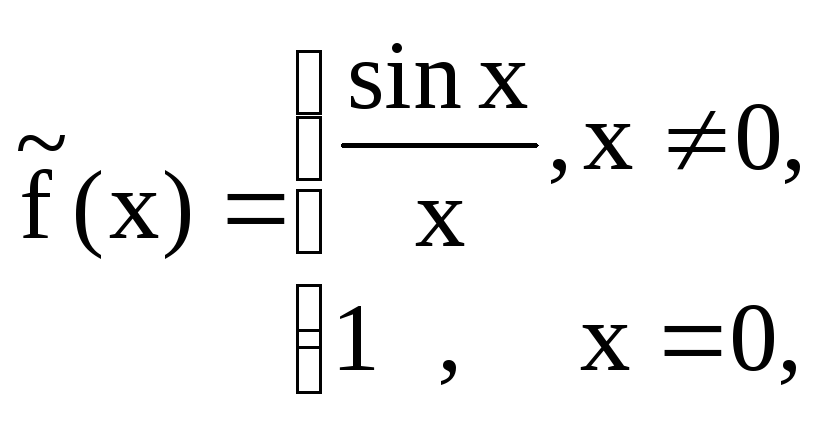то функциябудет всюду непрерывна.

2.Если, то точканазываетсяточкой разрыва первого рода функции.

3.Если хотя бы один из пределовне существует или равен бесконечности, то точканазываетсяточкойразрыва второго родафункции.

Свойства функций, непрерывных на отрезке

Определение.Функцияназывается непрерывной на отрезке, если она непрерывна во всех точках интервала (а,), непрерывна в точке а справа и в точкеслева.

Обозначение .

Осн.лит.: [11] Глава 1 § 1,2,3,4 стр. 9-38; Дополн.:25.

Контрольные вопросы:

1. Дайте определение функции. Что называется областью определения функции?

2. Какая функция называется бесконечно малой и каковы ее основные свойства?

3. Сформулируйте основные теоремы о пределах функций.

4. Приведите формулы замечательных пределов.

5.Дайте определение непрерывности функции в точке и на отрезке.

6. Какие точки называются точками разрыва функции.

Лекция 5. Дифференциальное исчисление. Основные определения и свойства производных и дифференциалов. Исследование поведения функций. Теоремы о среднем. Приложения производных в экономике.

Пусть в некоторой окрестности точки и в самой точке определена функция.

Определение.Если функцияопределена в некоторой окрестности точкии, то она называетсянепрерывнойв точке, где , .

В самом деле, этот предел означает, что , т. е..

Определение.Если существует предел, то это число называется производной функциив точке. Этот предел можно записывать также в виде.

Определение.Функцияназываетсядифференцируемойв точке, если она имеет конечную производную в этой точке.

Теорема.Если функциядифференцируема в точке, то она непрерывна в этой точке

Основные правила дифференцирования

Теорема 1.(правила дифференцирования суммы, произведения и частного). Если функцииидифференцируемы в точкеx, то сумма, произведение и частное этих функций (частное при условии, что) также дифференцируемы в этой точке и имеют место следующие формулы: 1. 2. 3.

Дифференцирование сложной функции. Пусть функциядифференцируема в точке,, функциядифференцируема в точке, тогда сложная функциядифференцируема ви её производная равна.

Для дальнейшего усвоения материала повторить таблицу производных основных элементарных функций.

С помощью этой таблицы и правил вычисления производных можно вычислить производную любой элементарной функции.

Понятие дифференциала функции

Определение.Если приращение функциив точкеможно представить в виде, где- число, а- б.м. при, то величинаназываетсядифференциаломфункциив точке(главной частью приращения).

Теорема (о дифференциале).Для того, чтобы функцияимела дифференциал в точке, необходимо и достаточно, чтобы существовала производная, при этом. (т.е.).

Схема исследования и построения графика функции

Чтобы исследовать функцию y=f(x) и построить ее график, действия рекомендуется проводить в следующем порядке.

1. Нахождение области определения функции. Исследование на четность, нечетность, периодичность. Нахождение точек пересечения графика с осями координат.

2. Исследование функции на непрерывность. Вычисление пределов функции при, стремящемся к границам области определения и к точкам разрыва.

3. Нахождение асимптот функции.

4. Вычисление f' (x) и исследование ее знаков. Нахождение интервалов возрастания, убывания и экстремумов.

5. Вычисление f''(x) и исследование ее знаков. Нахождение интервалов направления выпуклости и точек перегиба.

6. Построение таблицы, в которой указываются все найденные точки разрыва, критические точки первого и второго порядка и интервалы между ними. В каждом интервале характеризуется поведение функции.

7. Построение графика функции с учетом ее асимптот и таблицы. При необходимости можно вычислить промежуточные значения функции.

Приложение производной к экономике

В практике экономических исследований широкое применение получили производственные функции, используемые для установления зависимостей выпуска продукции от затрат ресурсов, при прогнозировании развития отраслей, при решении оптимизационных задач. В предположении дифференцируемости производственных функций важное значение приобретают их дифференциальные характеристики, связанные с производной. Так, если производственная функцияy=f(x) устанавливает зависимость выпуска продукцииу от затрат ресурсах, то f' (x) называютпредельным продуктом, если жеy=f(x) устанавливает зависимость издержек производствауот объема продукциих, тоf' (x) называютпредельными издержками.

Характеристикой относительного изменения прироста функции y=f(x) при малых относительных изменениях прироста аргументахявляетсяэластичность функции.Коэффициент эластичностиε определяется по формуле

или.

Коэффициент эластичности широко используют в исследованиях потребительского спроса на товары в зависимости от цен этих товаров или доходов потребителей. Высокий коэффициент эластичности означает слабую степень удовлетворения потребности; низкий указывает на то, что данная потребность высока.

Осн. лит.: 2, Глава 4 § 4.1-4.8, [127-150], [178-203], 12, 25.

Контрольные вопросы:

1. Производные основных элементарных функций.

2. Сформулируйте определение производной.

3. Сформулируйте определение дифференциала функции.

4. Дифференцирование сложной функции.

5. Изложите схему общего исследования функции и построения ее графика.

6. Приведите коэффициент эластичности.

Лекция 6.Первообразная. Неопределенный интеграл, его свойства. Основные методы интегрирования. Методы интегрирования некоторых функций. Приложения неопределенного интеграла в экономике

Определение.Первообразнойфункции, определенной в интервале, называется такая функция, производная которой совпадает св интервале, т.е. .

Теорема 1.Еслиидве первообразные функциина, то найдется такое числоC, что.

Из этой теоремы следует, что если есть одна первообразная функции, то любая другая ее первообразная имеет виддля некоторого числа.

Определение.Множество всех первообразных для функциина интерваленазывается еенеопределенным интегралом. Он обозначается символами, гдезнак интеграла,- дифференциал переменнойx.

Если какая либо первообразная функции, то,.

Свойства неопределенных интегралов

1) ;.

2) ;.

3) Если a- число, то.

4) .

5) Если ;,- числа, то

Например : .

Основные методы интегрирования