
- •Лекция 9. Обыкновенные дифференциальные уравнения первого порядка
- •2. Дифференциальные уравнения первого порядка
- •3. Уравнения с разделяющимися переменными Рассмотрим дифференциальное уравнение вида (4)
- •Общий интеграл его есть .
- •4. Однородные уравнения первого порядка
- •5. Линейные уравнения первого порядка.
- •6.Уравнения в полных дифференциалах
- •1. Линейные дифференциальные уравнения -го порядка
- •2. Линейный дифференциальный оператор и его свойства
- •3. Однородные линейные дифференциальные уравнения
- •4. Линейная независимость функций
- •5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •6. Метод Лагранжа (метод вариации произвольных постоянных)
- •7. Метод неопределенных коэффициентов
- •1. Числовые ряды. Сходимость и сумма рядов. Необходимый признак сходимости.
- •2. Достаточные признаки сходимости для рядов с положительными членами
- •3. Знакопеременные ряды. Признак сходимости Лейбница
- •Из (*) следует . (2)
- •Теорема умножения вероятностей:
- •Определение. Математическим ожиданием дсв х с законом распределения вероятностей
- •2.3 Планы практических занятий
6. Метод Лагранжа (метод вариации произвольных постоянных)
Пусть дано неоднородное ЛДУ
![]() -го
порядка
-го
порядка
![]() ,
(25)
,
(25)
где![]() .
.
Предположим, что найдена или известна
фундаментальная система решений
однородного уравнения
![]() .
Решением уравнения (25) будем искать в
виде
.
Решением уравнения (25) будем искать в
виде
![]() ,
(26)
,
(26)
т.е. предполагая
 не постоянными, а переменными и
дифференцируемыми на
не постоянными, а переменными и
дифференцируемыми на![]() величинами. Эти функции пока неизвестные
произвольные, для нахождения их нужно
иметь
величинами. Эти функции пока неизвестные
произвольные, для нахождения их нужно
иметь![]() условий. Продифференцируем
условий. Продифференцируем![]() еще раз
еще раз
![]() .
.
Предполагая каждый раз, что сумма в
квадратных скобках также равна нулю,
найдем
![]() производную
производную
![]()
![]() .
.
Полагая выражение в квадратных скобах равным нулю, продифференцируем
![]()
![]() .
.
Подберем
![]() так, чтобы функция (26) являясь решением
уравнения (25). Подставляя функцию (26) и
ее производные левую часть линейного
дифференциального уравнения (25), получим
так, чтобы функция (26) являясь решением
уравнения (25). Подставляя функцию (26) и
ее производные левую часть линейного
дифференциального уравнения (25), получим
![]() .
.
Так как
![]() -
частные решения однородного ЛДУ, то
получим последнее
-
частные решения однородного ЛДУ, то
получим последнее![]() условие относительно
условие относительно![]() .
Таким образом, для нахождения неизвестных
функций
.
Таким образом, для нахождения неизвестных
функций![]() получили систему линейных алгебраических
уравнений
получили систему линейных алгебраических
уравнений
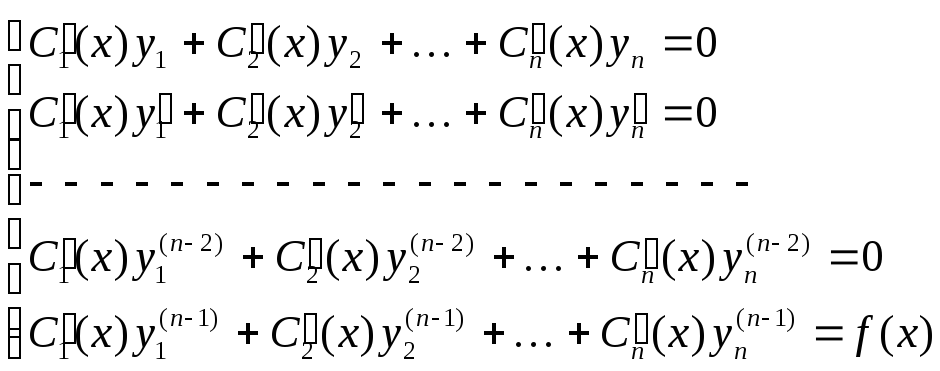 (27)
(27)
Решая ее методом Крамера (что можно
сделать, т.к. главный определитель
системы равен вронскиану
![]() ,
ибо
,
ибо![]() -
ФСР), имеем
-
ФСР), имеем![]() ,
,![]() ,
,
где определители
![]() получаются из главного
получаются из главного![]() заменой элементов
заменой элементов![]() -го
столбца свободными членами системы.
-го
столбца свободными членами системы.
Пример.Найдем общее решение
неоднородного ЛДУ второго порядка![]() .
.
Найдем вначале ФСР однородного уравнения
![]() .
Из характеристического уравнения
.
Из характеристического уравнения![]() получим
получим![]() ,
т.е.
,
т.е.![]() ,
,![]() ,
поэтому
,
поэтому![]() ,
,![]() .
Подставив эти функции в (27) получим
.
Подставив эти функции в (27) получим
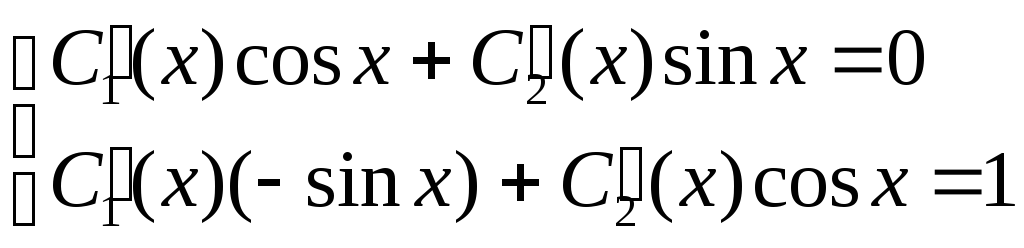
![]()
Отсюда
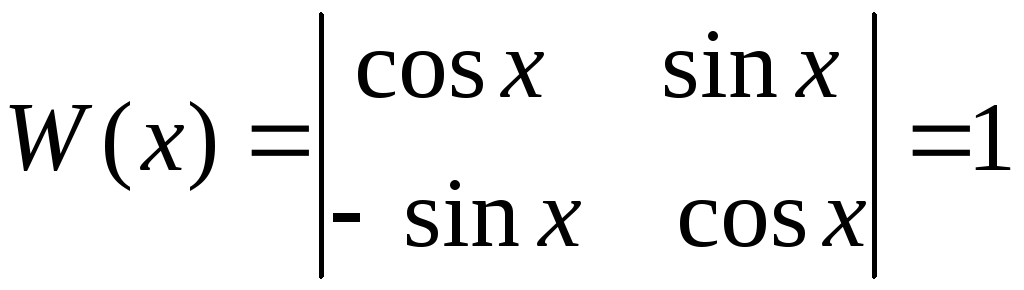 ,
, ,
,
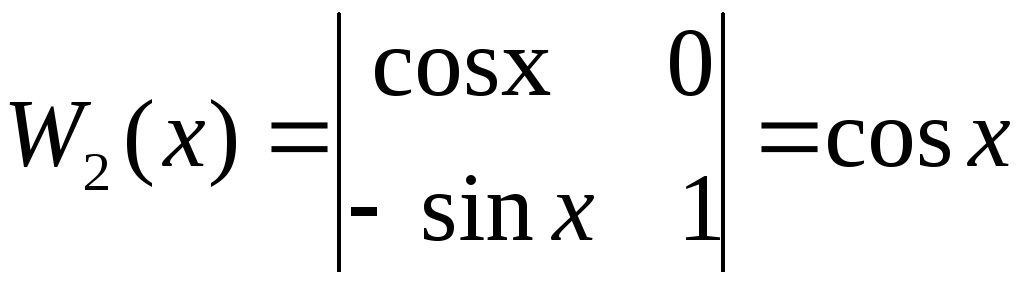 .
.
Следовательно
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
Окончательно получим общее решение
исходного уравнения
.
Окончательно получим общее решение
исходного уравнения![]() .
.
7. Метод неопределенных коэффициентов
Метод вариации можно использовать для любых линейных дифференциальных уравнений с любой непрерывной правой частью. А метод неопределенных коэффициентов можно применять только для уравнений с постоянными коэффициентами и только с правой частью определенных видов. Преимущество этого метода в том, что можно находить частное решение неоднородного уравнения, не прибегая к операции интегрирования.
Рассмотрим неоднородное ЛДУ
![]() -го
порядка с постоянными коэффициентами
-го
порядка с постоянными коэффициентами
![]() .
(28)
.
(28)
1) Пусть правая часть
![]() ,
где
,
где![]() -
многочлен степени
-
многочлен степени![]() .
.
а) Если
![]() не является корнем характеристического
уравнения, тогда частное решение
неоднородного уравнения ищется в той
же форме, т.е.
не является корнем характеристического
уравнения, тогда частное решение
неоднородного уравнения ищется в той
же форме, т.е.
![]() ,
,
где
![]() -
не определены. Для их нахождения нужно
продифференцировать
-
не определены. Для их нахождения нужно
продифференцировать![]()
![]() -
раз и подставить его в уравнение (28). А
дальше коэффициенты находятся аналогично
способу неопределенных коэффициентов
при интегрировании, т.е. приравниваются
коэффициенты при одинаковых степенях
-
раз и подставить его в уравнение (28). А
дальше коэффициенты находятся аналогично
способу неопределенных коэффициентов
при интегрировании, т.е. приравниваются
коэффициенты при одинаковых степенях![]() .
.
б) Пусть
![]() является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности![]() .
Тогда частное решение ищется в той же
форме, но с сомножителем
.
Тогда частное решение ищется в той же
форме, но с сомножителем![]() ,
т.е.
,
т.е.
![]() .
.
И далее аналогично пункту а).
2) Пусть правая часть уравнения (28) есть
![]() .
.
а) Если комплексное число
![]() не является корнем характеристического
уравнения, тогда частное решение
неоднородного уравнения ищется в виде
не является корнем характеристического
уравнения, тогда частное решение
неоднородного уравнения ищется в виде
![]() ,
,
где
![]() -
многочлены степени
-
многочлены степени![]() с неопределенными коэффициентами;б) Если
с неопределенными коэффициентами;б) Если![]() является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности![]() ,
тогда частное решение неоднородного
ЛДУ (28) ищется в виде
,
тогда частное решение неоднородного
ЛДУ (28) ищется в виде
![]() ,
,![]() .
.
3) Пусть правая часть неоднородного ЛДУ
представляет сбой сумму нескольких
функций, т.е.
![]() .
Для наглядности рассмотрим, когда правая
часть сумма двух функций
.
Для наглядности рассмотрим, когда правая
часть сумма двух функций![]() .
Решение будем искать в виде
.
Решение будем искать в виде![]() .
Тогда, подставляя его в уравнение и
пользуясь свойством линейного
дифференциального оператора, получим
.
Тогда, подставляя его в уравнение и
пользуясь свойством линейного
дифференциального оператора, получим![]()
или
![]() .
Таким образом, если правая часть
уравнения представляет собой сумму
.
Таким образом, если правая часть
уравнения представляет собой сумму![]() функций, то уравнение разбивается на
функций, то уравнение разбивается на![]() уравнений с этими новыми правыми частями.
Найдя частное решение каждого неоднородного
уравнения, получим частное решение
исходного уравнения в виде суммы частных
решений этих
уравнений с этими новыми правыми частями.
Найдя частное решение каждого неоднородного
уравнения, получим частное решение
исходного уравнения в виде суммы частных
решений этих![]() уравнений.
уравнений.
Основная литература: 3; 4, том 2. Дополнительная: 23.
Контрольные вопросы.
1. Укажите виды дифференциальных уравнений первого и второго порядка.
2. Дайте определение однородной функции
степени
![]() .
.
3. Приведите способы решения линейного дифференциального уравнения 1- порядка.
4. Что такое вронскиан?
Лекция 11. РЯДЫ. Основные определения и свойства числовых рядов. Признаки их сходимости. Степенные ряды, интервал сходимости. Теорема Абеля. Ряды Тейлора иФурье.
