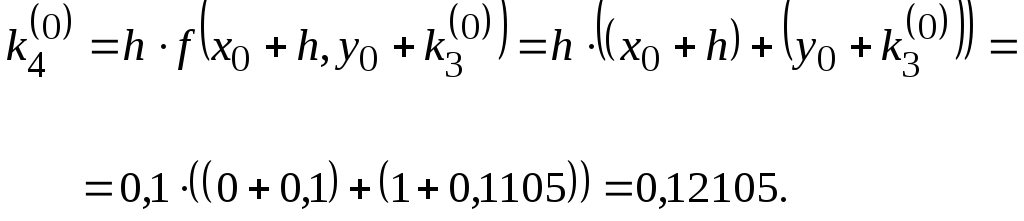Аналогично определяем отрезки ,, …

Как видно из рис.3, решение по методу Эйлера представляет собой ломаную . . . (так называемаяломаная Эйлера). Звенья этой ломаной в каждой вершинеимеют направление, совпадающее с направлением интегральной кривой уравнения (4), проходящей через точку.

Из рис.3 также видно, в методе Эйлера есть только единственное точное решение это. Длярасхождениеравняется(точное решение для), длярасхождениесоставит(точкана рис.3 не обозначена), таким образом, расхождение с каждым шагом накапливается. (Пример на решение дифференциального уравнения по методу Эйлера приведен ниже).

y

hhh

О

Рис. 3

Замечания к методу Эйлера.

Замечание 1. Метод Эйлера и его модификации являются простейшими представителямиконечно-разностныхметодов (шаговых методов) для приближенного решения обыкновенных дифференциальных уравнений.

Замечание 2. Доказывается, что если правая частьуравнения (4) непрерывна, то последовательность ломаных Эйлера прина достаточно малом отрезкеравномерно стремится к искомой интегральной кривой.

Замечание 3. Метод Эйлера имеет малую точность: с разложением Тейлора согласуется вплоть до, поэтому для получения большей точности необходимо уменьшить шаг, но это приводит к увеличению объема вычислений.

Замечание 4. Ошибки систематически накапливаются.

Замечание 5. Метод позволяет начать счет приi= 0 по известным начальным значениям.

Замечание 6. В этом методе можно изменить шаг в любой точке в процессе счета, что позволяет строить численные алгоритмы с автоматическим выбором шага.

Замечание 7. Как мы уже отмечали, на рис. 3 кривая, проходящая через точку, есть точное решение задачи Коши. И касательнуюмы проводим именно к этой кривой. Точка же, полученная в результате решения методом Эйлера, из-за его погрешности принадлежит ужедругой интегральной кривой (чтобы не насыщать рис. 9 дополнительными деталями, эта кривая не обозначена). Поэтому касательнаяв точкепроводится уже к этой новой кривой. Таким образом, погрешность метода Эйлера приводит к тому, что на каждом шаге решение переходит на другую интегральную кривую.

Замечание 8. Метод Эйлера легко распространяется на системы дифференциальных уравнений.

Метод РунгеКутта

Одним из наиболее употребительных одношаговых методов повышенной точности для решения обыкновенных дифференциальных уравнений (включая системы обыкновенных дифференциальных уравнений) является метод РунгеКутта. Метод РунгеКутта в некоторых задачах применяется для вычисления первых нескольких табличных значений функции, продолжаемых далее различными методами (например, многошаговыми или последовательных приближений, которые здесь не рассматриваются).

Наиболее употребительной является схема РунгеКуттачетвертого порядка. Запишем алгоритм этого метода в виде

, (10)

где

(11)

, (12)

Таким образом, метод РунгеКутта требует на каждом шаге четырехкратного вычисления правой части уравнения.

В предыдущем параграфе мы рассмотрели метод Эйлера. Метод Эйлера и его модифицированные варианты могут рассматриваться как методы РунгеКутта первого и второго порядков. Метод РунгеКутта требует большего объема вычислений, однако это окупается повышенной точностью, что дает возможность проводить счет с большим шагом. Другими словами, для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе РунгеКутта.

Для контроля правильности выбора шага используется следующее правило:

При каждом вычисляется дробь

.

Если Aбольше нескольких сотых, т.е. больше нескольких процентов, следует уменьшить шагh(обычно следующий шаг берутh / 2).

Погрешность метода РунгеКутта пропорциональна, гдеnпорядок метода (так как здесь мы рассматриваем метод РунгеКутта четвертого порядка, погрешность для него будет порядка), хотя точных способов оценки погрешности нет, и это является недостатком метода. Для грубой оценки погрешности метода применяют так называемыйпринцип Рунге. Согласно Рунге, величину погрешности вычисляют при помощи двойного счета

,

где значение функции, вычисленное с шагомh/2;вычисленное значение с шагомh.

Отметим, метод РунгеКутта прине используется.

Пример.а. Методом РунгеКутта вычислить на отрезке [0; 0,5] интеграл дифференциального уравнения:

, (13)

приняв шаг h= 0,1.

Решение.

Покажем начало процесса.

Вычисление . Последовательно имеем (12):

,