
- •Технических систем
- •Общие методические указания
- •Использование закономерностей
- •Распределение параметров по наработке
- •Расчет параметров распределения ресурса деталей автомобиля по результатам инженерных наблюдений
- •Значения ресурса l , тыс. Км
- •Шкала интервалов и частота попадания в интервал
- •Параметры распределения
- •Определение статистики 2
- •Вариационный ряд значений ресурса l, тыс. Км (значения расставлены по возрастанию)
- •Шкала интервалов и частота попадания в интервал
- •Расчетные параметры распределения
- •Объединенный интервальный ряд
- •Расчет статистики 2
- •Расчет показателей эффективности
- •Станции технического обслуживания
- •Автомобилей
- •Как системы массового обслуживания
- •Параметры сто
- •Решение
- •Решение
- •Решение
- •Нормированная функция нормального распределения
- •Плотность вероятности нормального распределения
- •И числа степеней свободы k
- •Значение функции
- •О главление
Шкала интервалов и частота попадания в интервал
|
Номер интервала |
Границы интервалов, тыс. км |
Середины интервалов lr, тыс. км |
Частота попадания в интервал, ni |
|
1 2 3 4 5 6 7 8 |
48,8…83,8 83,8…118,8 118,8…153,8 153,8…188,8 188,8…223,8 223,8…258,8 258,8…293,8 293,8…328,8 |
66,3 101,3 136,3 171,3 206,3 241,3 276,3 311,3 |
1 4 6 21 20 12 1 1 |
О пределение
характеристик нормального распределения.
Плотность вероятности имеет вид
пределение
характеристик нормального распределения.
Плотность вероятности имеет вид
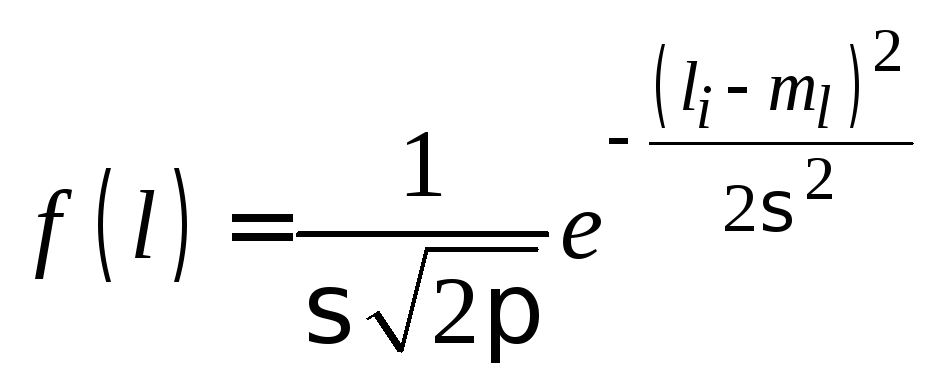 .
.
Статистические характеристики теоретического распределения оцениваем по результатам испытаний:
математическое ожидание (для интервального вариационного ряда, табл. 2.6)
![]()
![]()
![]() ;
;
среднеквадратическое отклонение (для интервального вариационного ряда)
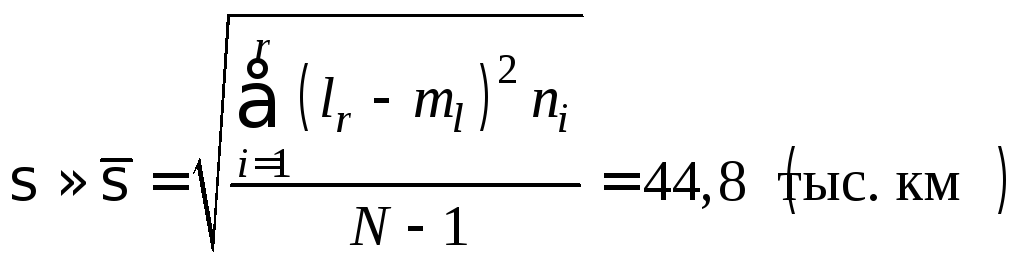 ;
;
значения
эмпирической плотности распределения
вероятностей
![]() по интервалам наработки (табл. 2.7):
по интервалам наработки (табл. 2.7):
![]() ;
;
нормированные
и центрированные отклонения середины
интервалов
![]() (табл. 2.7):
(табл. 2.7):
![]() ;
;
 значения теоретической
плотности распределения вероятностей
значения теоретической
плотности распределения вероятностей
![]() (табл. 2.7):
(табл. 2.7):
![]() ,
,
где
![]() – плотность вероятности нормального
распределения (табл. П2 Приложения).
– плотность вероятности нормального
распределения (табл. П2 Приложения).
Т а б л и ц а 2.7
Расчетные параметры распределения
|
|
|
|
|
|
|
n1
n2
n3
n4
n5
n6
n7
n8 |
–2,746
–1,964
–1,183
–0,402
0,379
1,161
1,942
2,723 |
0,0004
0,0017
0,0026
0,0091
0,0087
0,0052
0,0004
0,0004 |
0,0092
0,0579
0,1982
0,3680
0,3710
0,2036
0,0603
0,0099 |
0,0002
0,0013
0,0044
0,0082
0,0083
0,0045
0,0013
0,0002
|
по результатам
расчета строятся гистограмма, графики
![]() и
и![]() (рис. 2.2).
(рис. 2.2).
Проверка согласия между эмпирическим и теоретическим (нормальным) распределениями по критерию Пирсона. Как следует из анализа интервального вариационного ряда (табл. 2.6), для применения критерия Пирсона необходимо объединить интервалы 1 и 2, интервалы 7 и 8 с интервалом 6, так как в интервалах 1, 2, 7, 8 количество наблюдений менее 5. В результате объединения получим следующий ряд распределения (табл. 2.8).

Т а б л и ц а 2.8
Объединенный интервальный ряд
|
Интер- валы |
48,8…118,8 |
118,8… 153,8 |
153,8… 188,8 |
188,8… 223,8 |
223,8… 328,8 |
|
mi = ni |
5 |
6 |
21 |
20 |
14 |
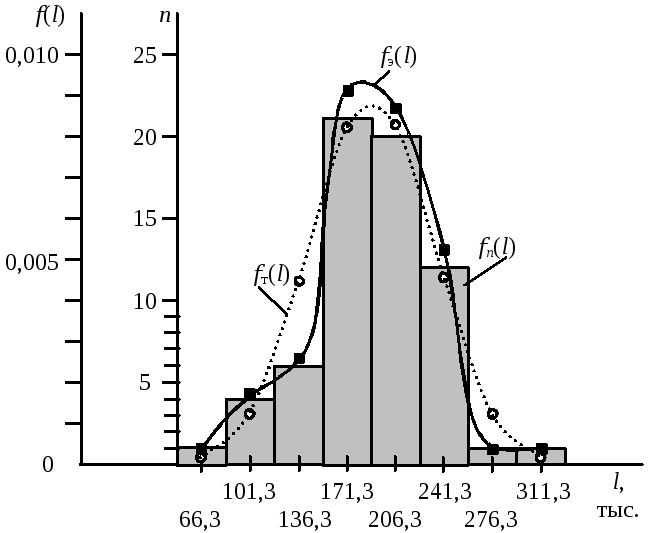
Рис. 2.2
Определим вероятность
![]() .
Вероятностьр1
выражает вероятность того, что случайная
величина Х,
имеющая
нормальный закон распределения, принимает
значение, принадлежащее интервалу
(48,8…118,8), т.е.
.
Вероятностьр1
выражает вероятность того, что случайная
величина Х,
имеющая
нормальный закон распределения, принимает
значение, принадлежащее интервалу
(48,8…118,8), т.е.
![]()

![]()
![]()
![]()
![]()
где Ф (t) определяется по табл. П4 Приложения. Аналогично получаем:
![]() ;
;
![]() ;
;![]() ;
;![]() .
.
Для нахождения
статистики
![]() составим табл. 2.9.
составим табл. 2.9.
Т а б л и ц а 2.9
Расчет статистики 2
|
№ п/п |
Интервал после объединения |
mi |
рi |
nрi |
|
|
|
|
1 |
48,8…118,8 |
5 |
0,0574 |
3,79 |
1,21 |
1,46 |
0,385 |
|
2 |
118,8…153,8 |
6 |
0,1565 |
10,33 |
4,33 |
18,75 |
1,815 |
|
3 |
153,8…188,8 |
21 |
0,2813 |
18,57 |
2,43 |
5,90 |
0,318 |
|
4 |
188,8…223,8 |
20 |
0,2834 |
18,70 |
1,30 |
1,69 |
0,090 |
|
5 |
223,8…328,8 |
14 |
0,2197 |
14,50 |
0,50 |
0,25 |
0,017 |
|
|
|
66 |
0,9983 |
65,89 |
|
|
2,625 = 2 |
Количество
интервалов r
= 5, количество параметров распре-деления
![]() –s
= 2, число
степеней свободы k
= r
– s
– 1 =
= 5 – 2 – 1 = 2. В табл. П3 Приложения
для уровня значимости
–s
= 2, число
степеней свободы k
= r
– s
– 1 =
= 5 – 2 – 1 = 2. В табл. П3 Приложения
для уровня значимости
![]() иk
= 2 соответствует
иk
= 2 соответствует
![]() .
Имеем 9,2 > 2,625, следовательно, нет
оснований отвергнуть гипотезу о
нормальности распределения ресурса.
.
Имеем 9,2 > 2,625, следовательно, нет
оснований отвергнуть гипотезу о
нормальности распределения ресурса.
В ероятность
безотказной работы детали.
Значение среднего ресурса R
при нормальном распределении численно
равно математическому ожиданию:
ероятность
безотказной работы детали.
Значение среднего ресурса R
при нормальном распределении численно
равно математическому ожиданию:
R = ml = 189,3 тыс. км.
Рассчитаем вероятность безотказной работы детали по интервалам наработки (табл. 2.6) по формуле
![]() ;
;
P(l1) = (66 – 1)/66 = 0,98; P(l2) = (66 – 5)/66 = 0,92;
P(l3) = (66 – 11)/66 = 0,83; P(l4) = (66 – 32)/66 = 0,52;
P(l5) = (66 – 52)/66 = 0,21; P(l6) = (66 – 64)/66 = 0,03;
P(l7) = (66 – 65)/66 = 0,015; P(l8) = (66 – 66)/66 = 0.
Н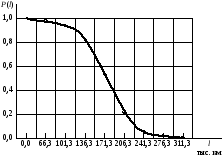 а
рис. 2.3 построена кривая вероятности
безотказной работы деталиP(l)
в зависимости от наработки l.
а
рис. 2.3 построена кривая вероятности
безотказной работы деталиP(l)
в зависимости от наработки l.
Рис. 2.3

З А Д А Ч А 3
