Задачи для самостоятельного решения

1. Векторы ивзаимно перпендикулярны; векторобразует с ними углы, равные; зная, что, вычислить:

1); 2); 3).

Ответ. 1) – 62, 2) 162, 3) 373.

2. Доказать справедливость тождества и выяснить его геометрический смысл.

3. Векторы попарно образуют друг с другом углы, каждый из которых равен. Зная, что, определить модуль вектора.

Ответ. .

4. Векторы иобразуют угол; зная, чтовычислить угол между векторами и.

Ответ. .

5. Даны векторы вычислить: 1), 2), 3), 4), 5) , 6) .

Ответ. 1) 22, 2) 6, 3) 7, 4) –200, 5) 129, 6) 41.

6. Даны точки А(–1,3,–7), В(2,–1,5), С(0,1,–5).

Вычислить 1), 2), 3), 4) найти координаты вектораи.

Ответ. 1) –524, 2) 13, 3) 3, 4) и.

7. Даны вершины четырёхугольника А(1,–2,2), В(1,4,0), С(–4,1,1), D(–5,–5,3). Доказать, что его диагонали АС и BD взаимно перпендикулярны.

8. Найти вектор , коллинеарный векторуи удовлетворяющий условию.

Ответ. .

9. Даны два вектора . Найти векторпри условии, что он перпендикулярен к осиOz и удовлетворяет условиям .

Ответ. .

10. Найти проекцию вектора на ось, составляющую с координатными осямиOx, Oz углы и, а с осьюOy – острый угол .

Ответ. –3.

11. Даны три вектора: Вычислить.

Ответ. –11.

12. Вычислить длину диагоналей параллелограмма, построенного на векторах , если известно, чтои угол между ними.

Ответ. 15, .

13. Вычислить , еслии угол между ними.

Ответ. .

14. Найти длины сторон и величины углов треугольника с вершинами ,В(–4,–2,0), С(3,–2,1).

Ответ. ,,,,.

15. Для заданных векторов вычислить

а)

б)

Ответ. а) , б).

16. Найти косинус угла  между диагоналями АС и BD параллелограмма, если заданы три его вершины А(2,1,3), В(5,2,–1) и С(–3,3,–3).

Ответ. .

17. Даны векторы ,и. Найти, если,,.

Ответ. .

§ 3. Векторное произведение векторов

Основные теоретические сведения

Определение. Векторным произведение вектора на векторназывается такой вектор, который удовлетворяет следующим трем условиям:

1. и, т.е. векторперпендикулярен плоскости, в которой можно расположить векторыи;

2. т.е. длина векторачисленно равна площади параллелограмма, построенного на векторахи;

3. упорядоченная тройка векторов – правая, т.е. если привести векторы к общему началу и смотреть с конца вектора, то кратчайший поворот откдолжен быть виден против часовой стрелки (рис. в табл.1).

Векторное произведение обозначают или. Из определения векторного произведения следует, например, что при, т.е. необходимым и достаточным условием равенства нулю векторного произведения является коллинеарность векторов.

Алгебраические свойства векторного произведения

1) ;

2) ;

3) .

Если векторы изаданы своими координатами в ортонормированном базисе(в декартовой системе координат), то векторное произведение в том же базисе вычисляется так:

, .

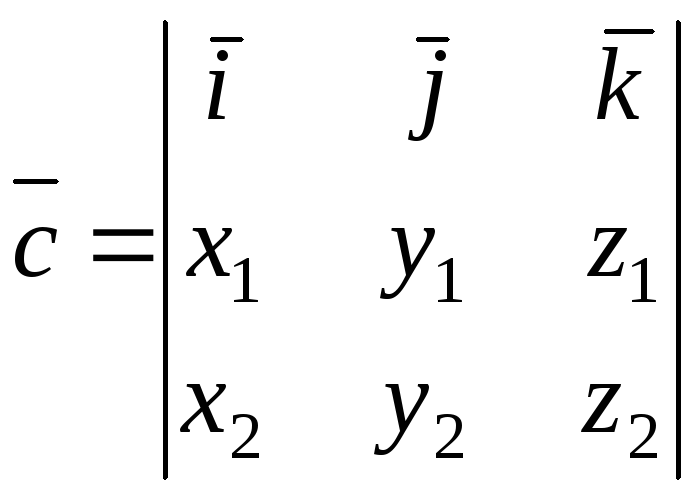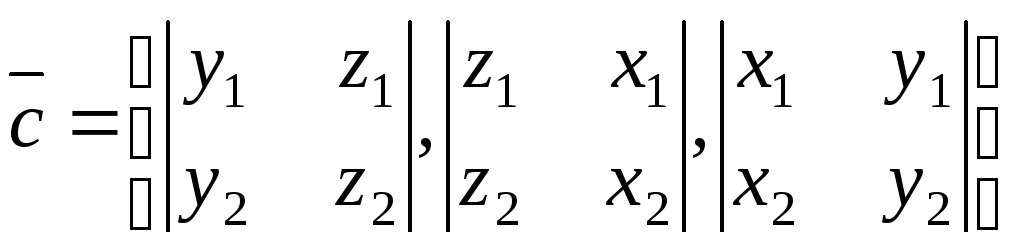Векторное произведение векторов широко используется в геометрии, механике, физике, теории поля и т.д.

Примеры решения задач

Задача 3.1. Дано: ;и. Вычислить:

1. ;

2. ;

3. .

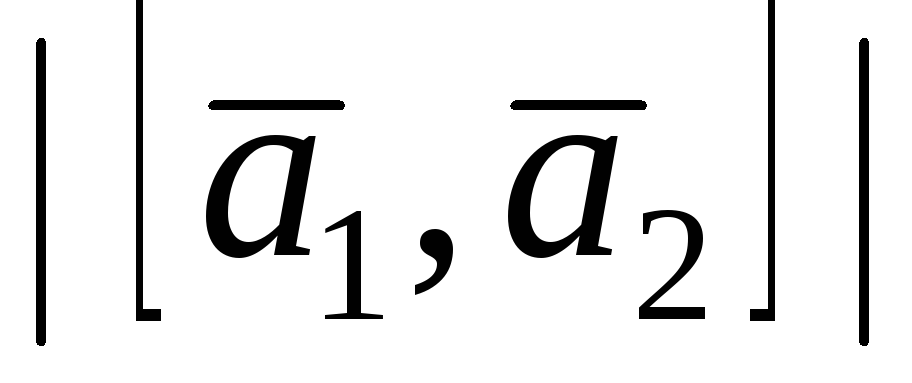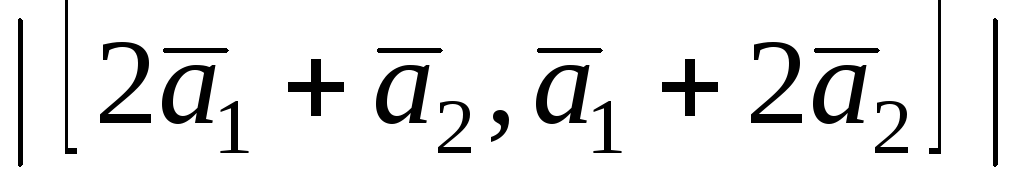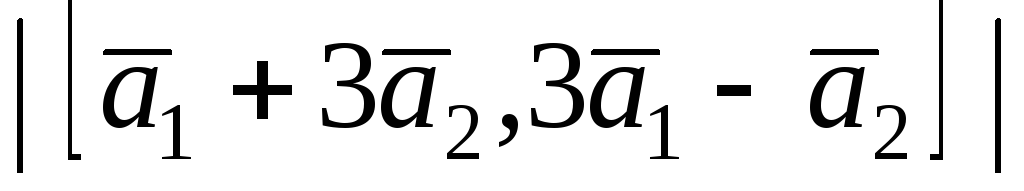Решение.

1. По определению .

Ответ. .

2. Используя свойства векторного произведения, преобразуем произведение .

Следовательно, .

Ответ. .

3. Аналогично

.

Ответ. .

Задача 3.2. Дано: ,и. Вычислить.

Решение. По определению скалярного произведения .

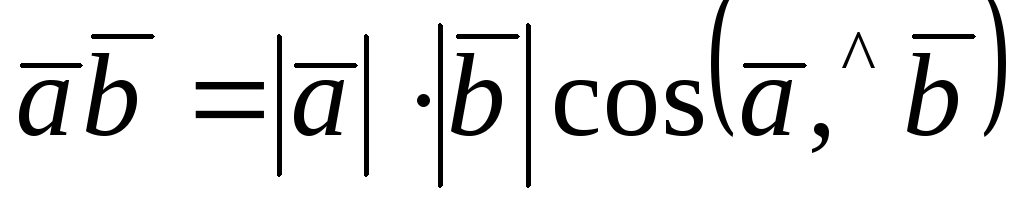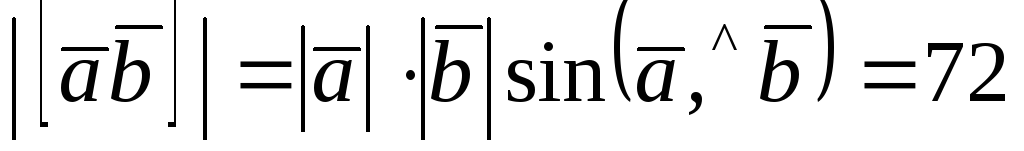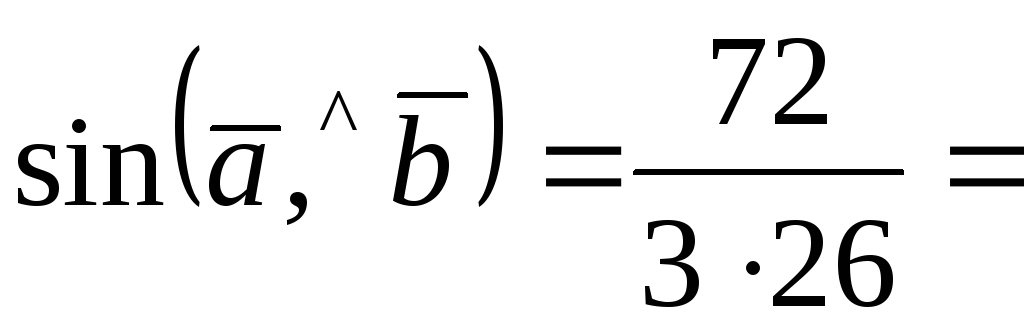
По условию , следовательно,. Тогда.

Таким образом, .

Ответ. .

Задача 3.3. Какому условию должны удовлетворять ненулевые векторы и, чтобы векторыибыли коллинеарны?

Решение. Если векторы коллинеарны, то их векторное произведение равно нулю, т.е. .

Следовательно, по свойствам векторного произведения векторы иколлинеарны (сонаправлены или противонаправлены).

Замечание. К такому же выводу можно прийти, если вспомнить, что сумма и разность двух векторов – это векторы, совпадающие с диагоналями параллелограмма, построенного на исходных векторах.

Ответ. .

Задача 3.4. Упростить выражения:

1. ;

2. ;

3. .

Решение.

1.

,

т.к. вектор совпадает по определению с вектором, ас вектором.

Ответ. .

2.

.

Ответ. .

3.

.

Здесь мы воспользовались свойством скалярного квадрата вектора.

Ответ. 3.

Задача 3.5. Дано: . Вычислить площадь треугольника, построенного на векторахи.

Решение. Площадь треугольника равна половине площади параллелограмма, построенного на тех же векторах. Следовательно: ,,

.

Ответ. .

Задача 3.6. Дано: ,. Найти координаты векторов:

1. ;

2. .

Решение.

Способ 1.

,

тогда

.

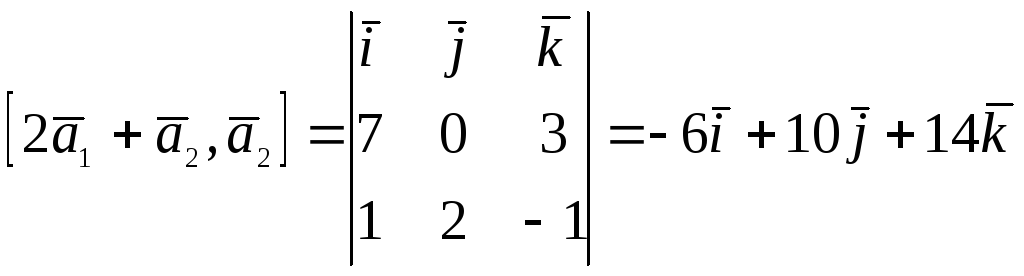Ответ. .

2. .

Тогда .

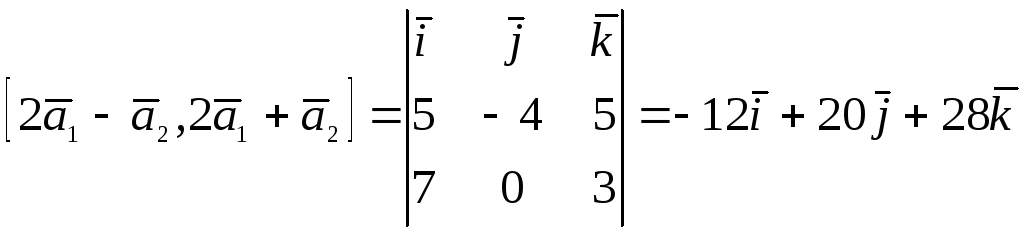Ответ. .

Способ 2. Можно, воспользовавшись свойствами векторного произведения, сначала преобразовать искомое произведение (как мы это делали в задача 3.3 и 3.4):

1. .

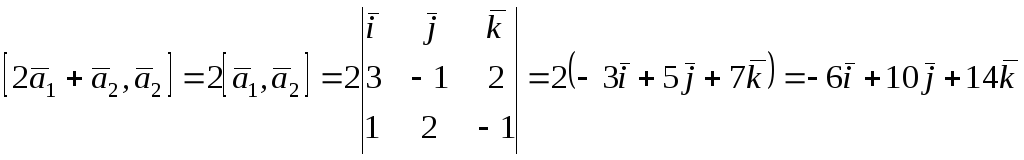2. Этот пункт решается аналогично.

Задача 3.7. В треугольнике с вершинами ,инайти.

Решение. Из определения векторного произведения имеем (рис. 1.18). С другой стороны,. Следовательно,,

.

Рис. 1.18

Аналогично ,;

,

.

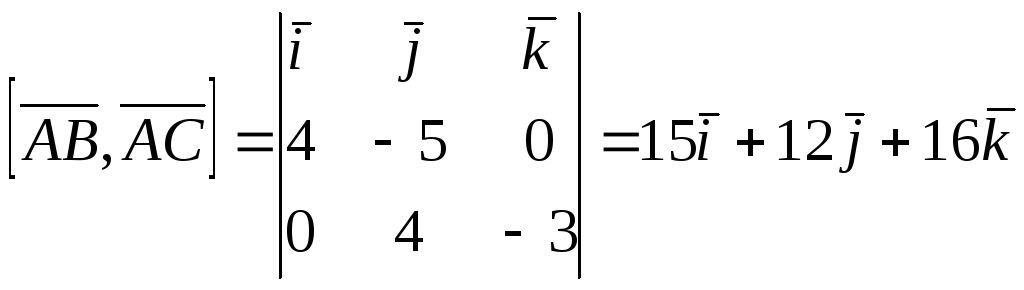Таким образом, .

Ответ. 5.

Задача 3.8. Сила приложена к точке. Определить момент этой силы относительно точки.

Решение. Если вектор изображает силу, приложенную к какой-либо точкеА, а вектор имеет начало в точкеО и конец в точке А, то вектор представляет собой момент силыотносительно точкиО. Таким образом, нам необходимо вычислить

.

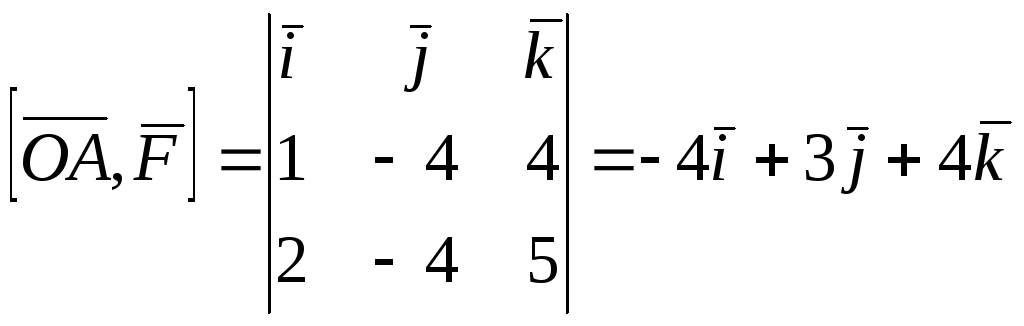Ответ. .

Задача 3.9. Найти координаты вектора , если известно, что он перпендикулярен векторами, образует с ортомтупой угол и.

Решение. По условию ,:

.

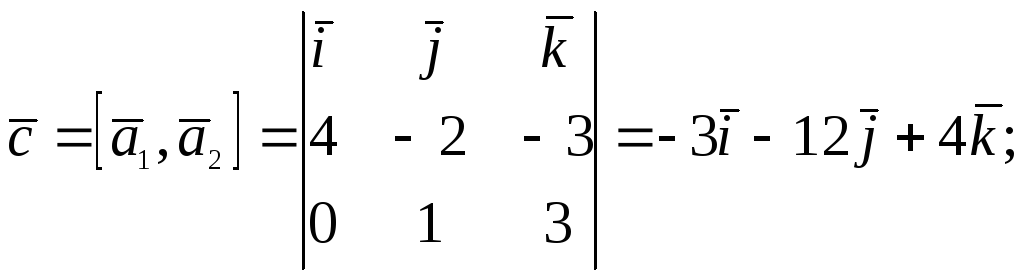
Вектор ,, причем, т.к. вектортак же, как и вектор, образует с ортомтупой угол (проекция векторана направление ортаравна отрицательному числу -12). Следовательно,. Итак,.

Ответ. .

Задача 3.10. Найти площадь параллелограмма, диагонали которого и. Угол между диагоналями.

Решение. По свойствам параллелограмма, известно: , а.

Тогда по условиям задачи ,.

Складывая и вычитая полученные уравнения, будем иметь

, .

Найдем векторное произведение, используя его свойства.

.

Площадь параллелограмма: .

Ответ. .

Задача 3.11. Даны векторы и, приложенные к общей точке. Найти орт биссектрисы угла между векторамии.

Решение. Найдем длины векторов и:

и .

Биссектриса совпадает с диагональю ромба, поэтому найдем орты векторов и, и сложим их:.

.

Длина вектора: .

Орт вектора :.

Ответ: .

Задача 3.12. Вектор перпендикулярный к осии вектору, образует острый угол с осью. Зная, что. Найти его координаты.

Решение.

Способ 1: Пусть .

по условию, т.к. , т.к.– острый угол;, т.е..

Составим систему уравнений и решим ее.

, ,

,

, ,

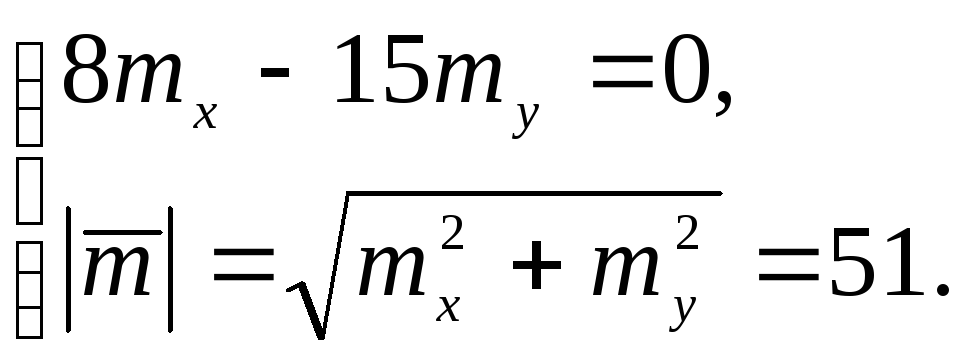
, не подходит, т.к.по условию.

Итак, .

Способ 2. Используем векторное произведение.

, ,,.

, вычислим вектор :

.

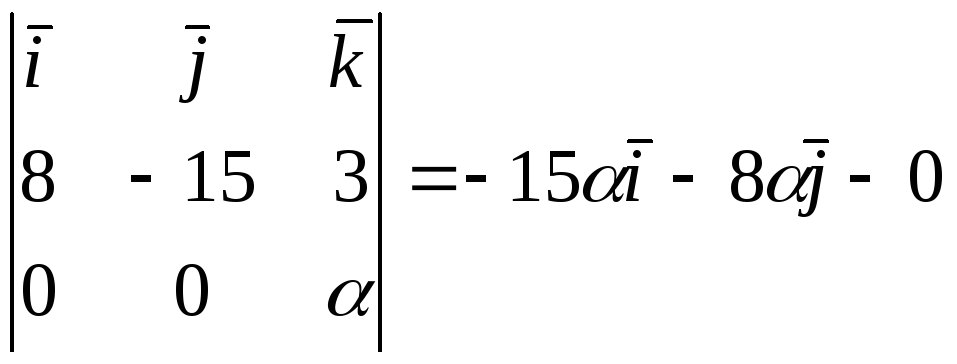Получили , по условию.

, подходит , т.к.по условию.

Итак, .

Ответ: .